Технические науки/3.Отраслевое машиностроение

Кондрашов С.Г., Кондрашова И.Г., Иванов И.В.

Херсонский национальный технический университет

Теоретическое исследование автоколебаний при резании

Рассмотрим случай обработки многолезвийным инструментом с механическим креплением двух пластин, расположенным рядом в одном корпусе и реализующим схему деления припуска, когда наиболее вероятно возникновение первичных автоколебаний и регенеративного эффекта вследствие отрицательной геометрии пластин 1и 2, ограниченной жёсткости державки и т.д. Расстояние между пластинами, измеренное по оси инструмента, равно Δ. Первая пластина работает с глубиной t₁, вторая t₂. Заготовка вращается с угловой скоростью ω₀, инструмент двигается вдоль оси со скоростью подачи S.

Предварительные исследования показали, что волнистость поверхности в этом случае обусловлена в основном колебаниями инструмента в радиальном направлении, поэтому для дальнейших рассуждений принимаем во внимание только колебания по оси y.

Автоколебания, обусловленные работой пластины 1, начинаются с начальной точки и могут быть вызваны любым случайным толчком, геометрией, ликвациями материала заготовки, падающей характеристикой силы резания и т.д. В результате инструмент образует волнистую поверхность, профиль которой соответствует развёртке колебаний системы во времени. Вторая пластина, начиная с точки 0, должна снимать стружку периодически меняющейся глубины (регенеративный эффект). Сила резания Р, а следовательно, и ее составляющая Р_у, периодически модулируется частой, равной частоте собственных колебаний системы. Возникают резонансные колебания, в связи с чем снова может возникнуть волнистая поверхность.

Установим взаимовлияние возникающих автоколебаний и их влияние на общие вибрации инструмента. Пусть колебательная система имеет массу m, жёсткость K, постоянную затухания С.

Положения режущей кромки инструмента относительно среднего положения при первом проходе принимаем через ось У₁, при втором через У₂, приняв направление вверх за положительное.

Глубина резания в каждый момент времени при снятии первой стружки:

t^΄₁=t₁-y₁

При снятии второй стружки:

t^΄₂=t₂-y₂+y₁

Силу резания выразим, используя коэффициент глубины r, который определяет степень воздействия процесса резания на колебательную систему и равен отношению приращения силы dp, действующей на колебательную систему, к величине деформации у, умноженному на косинус угла между плоскостью колебаний и плоскостью, перпендикулярной к режущей кромке.

В нашем случае величина r равна:

r =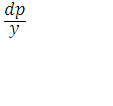 cosφ

где φ – главный угол в плане.

Сила резания равна Р=rt;

составляющая P_y=rtcosβ;

введя обозначение r_y=rcosβ;

будем иметь P_y=r_yt.

Уравнение колеблющейся массы для движения в направлении Y при работе первой пластины имеет вид:

my₁+cy₁+ky₁=P_ycp-r_yy₁

Постоянная сила P_ycp не влияет на характер колебаний, поэтому:

my₁+ су₁ + (г_у + k)y₁ = 0

Решение линейного однородного управления второго порядка ищем в виде:

y=e^dt, где d=const

Характеристическое уравнение имеет вид:

md²+cd+(k+r_y)=0

Корни этого уравнения, в общем случае комплексные, входят попарно сопряженными и равными:

d₁=-λ+Јω_y,

d₂=- λ-Јω_{y ,}

где λ=с/2m, .

Общий интеграл уравнения my₁+ су₁ + (г_у + k)y₁ = 0 в случае комплексных корней характеристического уравнения имеет вид:

y₁=e^-λt(A₀sinω_yt+B₀cosω_yt)

Подставив начальные условия t=0, y₁=v, получим:

y₁=A_ye^-λtsin(ω_yt+φ_y1)

Поскольку λ>0, то имеет место затухающее движение.

Таким образом, уравнение :

y₁=A_ye^-λtsin(ω_yt+φ_y1)

описывает форму волнистой поверхности после первого прохода.

Переменная глубина резания на втором проходе

t΄₂=y₁-y₂

Сила резания будет изменятся в зависимости от координаты согласно выражению:

P_y2=r_y(y₁-y₂)

Уравнение движения колебательной системы при втором проходе будет иметь вид:

my₂+cy₂+ky₂=(y₁-y₂)r_y ;

my₂+cy₂+(k+r_y)y₂=r_yy₁=r_y A_ye^-λtsin(ω_yt+φ_y1).

Следовательно, вид уравнения колебательного движения в направление OY при работе второго резца определяется тем, что левая часть его совпадает с левой частью уравнения для первой пластины, а в правой части находится интеграл этого уравнения, умноженный на r_y.

Введём обозначения:

f=r_yA_ye^-λt/m;

P=c/m;

q=(k+r_y)/m/

Тогда уравнение

my₂+cy₂+(k+r_y)y₂=r_yy₁=r_y A_ye^-λtsin(ω_yt+φ_y1)

примет вид:

y₂+py₂+qy₂=fsin(ω_yt+φ_y1)

Как известно , общее решение неоднородного уравнения представляется как сумма какого–нибудь частного решения этого уравнения и общего решения соответствующего однородного уравнения. Как было показано выше, общее решение однородного уравнения имеет вид:

₂= A_ye^-λtsin(ω_yt+φ_y2)

Частное решение неоднородного уравнения ищем в форме:

=Mcosβt+Nsinβt

В последнем выражении частота колебаний β равна частоте колебаний внешней силы P_y2. Как указывалось выше, причиной возникновения периодической внешней силы является регенеративный след на обработанной поверхности, профиль которого соответствует развёртке колебаний первой пластины во времени. Как было установлено в результате решения уравнения

my₁+ су₁ + (r_у + k)y₁ = 0

частота этих колебаний равна ω_y. Таким образом, сила P_y2 периодически

модулируется частотой ω_y, равной частоте колебаний первого резца. Иначе говоря , β=ω_y .

С учётом последнего выражения уравнения =Mcosβt+Nsinβt примет вид

=Mcos ω_yt +Nsin ω_yt

Подставляя это выражение в исходное дифференциальное уравнение, находим значения М и N:

М=-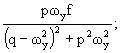

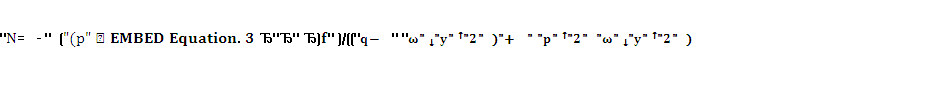
Прежде чем подставлять найденные значения М и N в равенство:

=Mcos ω_yt +Nsin ω_yt

введём новые постоянные А^* и φ, приняв:

М=А^*sinφ₂^*, N=A^*cosφ_y^*

т.е.

tgφ^*=M/N

Тогда частное решение неоднородного уравнения можно записать в форме:

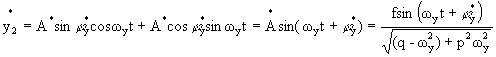
Общий интеграл уравнения y₂+py₂+qy₂=fsin[ω_yt+φ_y1] равен y₂= + ,т.е.

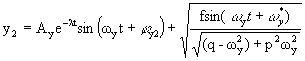
Обозначив

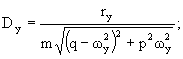
будем иметь

.

Уравнения колебательного движения для первого y₁=A_ye^-λtsin(ω_yt+φ_y1) и второго резцов выведены при условии, что они работают независимо друг от друга. Однако в рассматриваемом случае оба резца жестко закреплены в одном корпусе и, следовательно, результирующее колебательное движение У корпуса инструмента с резцами подчиняется принципу суперпозиции и будет равно сумме колебаний, возбуждаемых первой и второй пластинами, т.е.

y=y₁+y₂=A_ye^-λt (sinω_yt+sin(ω_yt+ψ_y)+D_ysin(ω_yt+φ^*_y))

где ψ_y=φ_y2-φ_y1 - сдвиг фаз между колебаниями первой и второй пластин.

С другой стороны, фазовый угол ψ_у можно представить в виде:

ψ_y=ω₀t₀

где t₀-время работы первой пластины до момента врезания второй, ω₀-угловая скорость вращения .В свою очередь t₀=L/V,

где L- путь резани, V- линейная скорость.

Эти величины выражаем следующим образом

L=n_x2πD/2

V=ω₀D/2

где n_x – число оборотов, которое совершит заготовка до момента врезания второго резца, D-диаметр обработки.

Число оборотов:

n_x=Δ/S

где Δ- расстояние между пластинами, S- подача в мм/об.

Подставив эти величины в уравнение ψ_y=ω₀t₀, получим:

c учётом выражения Ψ_y= общие колебания инструмента будут описываться уравнением:

Рассмотрим условия, при которых выражение обращается в нуль, т.е. отсутствуют вибрации инструмента. Очевидно, при наличии первых колебаний величина А_у будет всегда отлично от нуля. Поэтому для выяснения условий виброгашения приравняем к нулю выражение в скобках и режим его относительно ψ_у. Предварительные расчёты показывают, что величина D_y на два порядка меньше амплитуд первых двух синусоид, поэтому в дальнейших расчётах с большой степенью точности величиной D_ysin (ω_yt+φ_y^*) можно пренебречь.

Таким образом,

sin ω_yt+sin(ω_yt+2πΔ/s)=0

sin ω_yt=- sin(ω_yt+2πΔ/s)

откуда

где n-любое целое число.

Окончательно будем иметь: Δ/S= (2n+1)/2

Таким образом, последнее уравнение выражает условие виброгашения за счёт взаимной компенсации автоколебаний при реализации инструментом схемы деления припуска.

Литература:

1. Василенко Н.В. Теория колебаний: учебное пособие для студентов технических вузов. К.: Высш. шк., 1992 – 430 с.

2. Родин П.Р. Геометрия режущей части спирального сверла. К, 1971. 136с.

3. Кондрашов С.Г. Диссертация на соиск. уч. ст. канд. техн. наук. Киев, КПИ – 1990, - 250 с.