Карачун В.В., Мельник В.Н.

Национальный технический университет Украины «КПИ»

ПАРАМЕТРЫ ЛАМЕ И КРИВИЗНА ПОВЕРХНОСТИ ПОПЛАВКОВОГО ПОДВЕСА

Уточним соотношения для вычисления параметров Ламе А_1, А₂, а также кривизн и поплавкового подвеса в виде выпуклой (вогнутой) оболочки. Проводя дальнейшие исследования, принимаем обязательным выполнение условия – , - радиус, - подъем линии меридиана.

Параметр А₂ целесообразно представить в виде-

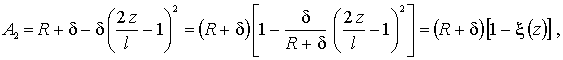(1)

где

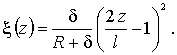
Легко установить, что функция при то есть

Параметр А₁ представим в виде-

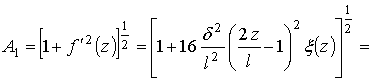
где

Окончательно значение параметра А₁ запишем так –

(2)

где

В дальнейшем считаем геометрию оболочки такой, для которой выполняется условие –

(3)

Это условие имеет ту привлекательность, что содержит характерные геометрические параметры.

Принимая во внимание условие (3), полагаем, что

(4)

Преобразуем соотношения для вычислений величин и . Имеем:

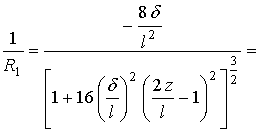
(5)

С учетом основного допущения (3), выражение (5) упрощается:

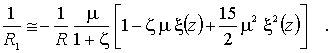(6)

Очевидно, что когда , тогда и , а, следовательно, и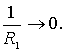

Остается найти значение кривизны . Имеем:

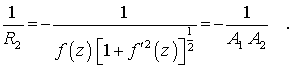
Принимая во внимание выражения (1) и (4), получаем:

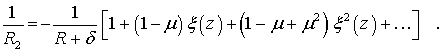(7)

Окончательно имеем:

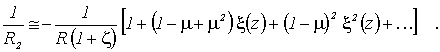
Если из формулы (7) получаем

что и должно иметь место.

Формулы (1), (4), (5) и (7) справедливы только при выполнении условия (3).

Проведем численную оценку возможной геометрии поплавка. Пусть Это достаточная выпуклость (или вогнутость) поверхности. Тогда:

Чтобы выполнялось условие (7) , необходимо при значительной выпуклости (или вогнутости) брать сравнительно протяженные оболочки.

Пусть . Тогда

Если

Последний случай наиболее неблагоприятный. Проанализируем для этого случая численные значения коэффициентов в выражениях (1), (4), (5), (7).

Прежде всего :

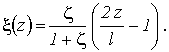
Тогда максимальное значение при и будет равно- .

Максимальное значение параметра А₁:

Максимальное значение параметра А₂:

.

Максимальное значение параметра :

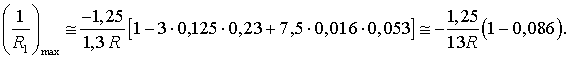
Максимальное значение параметра :

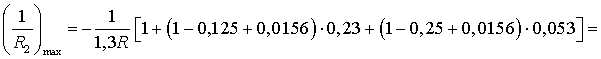
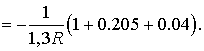
Таким образом, приведенные числовые расчеты дают право утверждать, что можно задать такие геометрические размеры поплавка, когда в параметрах А₁, А₂, и , начиная с третьего слагаемого, можно пренебрегать остальными.

Сделаем предположение, что

(8)

Тогда, согласно формулам (1, 2, 4), будем рассматривать случай, когда постоянные Ламе определяются соотношениями-

(9)

(10)

Упростим уравнения движения оболочки. Для этого, воспользуемся допущениями, сформулированными выше. Кроме того, в уравнениях, после вычислений, появятся слагаемые, содержащие множители

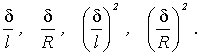
Присутствие последних двух, позволяет отбросить, ввиду малости, соответствующие слагаемые, так как

и.

Таким образом, все уравнения имеет смысл привести к следующей структуре:

внешнее возмущение + силы инерции.