Экономические науки /3.Финансовые отношения.

магістр Найдьонов А. Г.

Національний гірничий університет, Україна

ФОРМУВАННЯ ОПТИМАЛЬНОЇ СТРАТЕГІЇ БУДІВЕЛЬНОЇ

ОРГАНІЗАЦІЇ В УМОВАХ НЕВИЗНАЧЕНОСТІ

Одним із найважливіших елементів економічної системи є інвестиційно-будівельна галузь. Від її розвитку залежить соціально-економічне становище держави, забезпечення населення необхідним житлом та розширене відтворення основного капіталу підприємств. Сучасний стан галузі потребує негайних комплексних дій держави щодо підтримки й упровадження пріоритетних програм стратегічного розвитку інвестиційно-будівельного комплексу України. Основними їх завданнями є: підвищення інвестиційної привабливості будівельної галузі; стимулювання та впровадження науково-технічних досягнень, тобто інновацій у будівництві; розвиток та підтримка вітчизняних виробників будівельних матеріалів; удосконалення управління інвестиційно-будівельним проектом; формування ефективного механізму ціноутворення; створення сучасної виробничої бази; упровадження діючих механізмів залучення фінансово-кредитних коштів населення для вкладення їх у будівництво; комплексна підтримка держави щодо податкового законодавства, нормативної бази регулювання будівельної галузі України.

Ринковий механізм господарювання визначає багато важливих питань щодо функціонування будівельних підприємств. Одним із них є визначення оптимальної стратегії будівельної організації в умовах невизначеності попиту та формування виробничої діяльності, яка має задовольнити ринкову потребу. Вирішення цього питання забезпечить стабільне функціонування, подальший розвиток та підвищення прибутковості будівельної організації.

Існує достатньо багато підходів до вирішення цього питання. Проте досліджені підходи не завжди достатньо науково обґрунтовані, працюють при дуже жорстких обмеженнях та мають досить трудомісткий алгоритм виявлення оптимальних рішень. У дослідженні [1] запропонована методологія знаходження коефіцієнта економічної рівноваги підприємства, який передбачає, що попит на продукцію відомий, і відношення прибутку до обсягу виробництва постійне як для галузі, так і для підприємства. В іншій роботі [2] запропонована модель вірогідності, яка ґрунтується на аналізі впливу статистичних характеристик економічних показників на вірогідність інтегральних показників стійкості підприємства.

Тому метою дослідження, результати якого викладені в доповіді є обґрунтування методології знаходження оптимальної стратегії підприємства будівельної галузі в ринкових умовах, яка заснована на теорії ігор.

Задача полягає у визначенні оптимальної стратегії підприємства (оптимальної кількості об’єктів будівництва), яка гарантує максимальний середній рівень доходу при будь-якому стані попиту, вважаючи його невизначеним.

Будівельне підприємство реалізує m видів будівельних об’єктів. Збут об’єктів залежить від попиту, який може бути в одному з n станів. За даними минулих спостережень, підприємство може реалізувати kij об’єктів i-го виду в умовах j-го стану попиту ( i = 1, 2, ..., m; j = 1, 2, ..., n ). Відомі витрати zi та ціна реалізації ri одного об’єкта i-го виду ( i = 1, 2, ..., m).

Основні показники цього завдання можна подати таким чином: kij – обсяг реалізованих будівельно-монтажних робіт i-го виду в умовах j-го стану попиту ( i = 1, 2, ..., m; j = 1, 2, ..., n ); zi і ri – капіталовкладення та ціна реалізації об’єкта i-го виду ( i = 1, 2, ..., m) відповідно.

Найбільш привабливим економіко-математичним методом вирішення цієї проблеми є метод теорії ігор. Гра, у цьому випадку, відноситься до парної гри p нульовою сумою (виграш одного із гравців дорівнює програшу іншого) [3].

Будівельне підприємство (гравець А) має декілька стратегій: стратегія Ai –будівництво об’єктів із розрахунку на i-й стан попиту ( i = 1, 2, ..., n ). Попит розглядатимемо як другого гравця (гравець B) з n стратегіями: стратегія Bj – попит в j-му стані ( j = 1, 2, ..., n ).

Знаходимо дохід підприємства aij , якщо воно здійснює будівництво з розрахунку на i-й стан попиту, а насправді попит знаходиться в j-му стані.

Якщо i = j , тобто розрахунки підприємства збігаються з дійсністю, то дохід підприємства визначається за формулою:

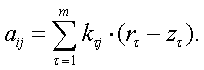
(1)

Якщо i ≠ j , тобто розрахунки не збігаються з дійсністю, то дохід підприємства дорівнює різниці прибутку від фактично реалізованих будівельних об’єктів та витрат через відсутність попиту на частину побудованих об’єктів, тобто

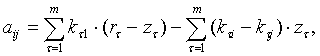(2)

де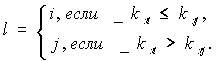

У результаті одержуємо платіжну матрицю даної гри P = (aij)( i, j = 1, 2, ..., n) – матрицю доходів будівельного підприємства. У табл. 1 подано її загальний вигляд.

Таблиця 1

Матриця доходів будівельного підприємства

	B1	B2	…	Bn
A1	a11	a12	…	a1n
A2	a21	a22	…	a2n
…	…	…	…	…
An	an1	an2	…	ann

При визначенні оптимальної стратегії підприємства керуємося «максимальним критерієм» – максимальний гарантований середній рівень доходу.

Принцип рішення гри: стратегії: і першого і другого гравця відповідно називаються їх оптимальними стратегіями, а число v – ціною гри, якщо для будь-якої стратегії SA першого гравця і будь-якої стратегії S8 другого гравця виконуються нерівності:

, (3)

де M – математичне очікування виграшу (середній виграш) першого гравця, якщо першим і другим гравцями вибрані відповідно стратегії і .

Із нерівності (3) випливає, що . Це означає, що ціна гри дорівнює математичному очікуванню виграшу першого гравця, якщо обидва гравці виберуть оптимальні для себе стратегії, тобто стратегії, при яких гравець А одержить максимальний гарантований (не залежний від поведінки гравця В) виграш, а гравець В доб’ється мінімального гарантованого (незалежно від поведінки гравця А) програшу.

Рішення цієї гри може бути зведено до вирішення завдання лінійного програмування.

Запропонований алгоритм економіко-математичного знаходження оптимальної стратегії підприємства будівельної галузі в ринкових умовах дозволив зробити такі висновки:

запропонована математична модель, дозволяє визначити оптимальну стратегію виробництва будівельного підприємства на основі урахування невизначеності попиту для підвищення ефективності їх функціонування в сучасних умовах;

алгоритм вирішення проблеми дослідження може бути достатньо просто реалізовано за допомогою комп’ютерного програмного продукту EXCEL.

Література:

1. Жучков Г.А. Оцінка і прогнозування економічної рівноваги підприємства будівельної галузі / Г.А. Жучков, В.А. Оченаш, О.В. Патенко // Регіональні перспективи. – 2001. – № 5-6 (18-19). – С. 293-294.

2. Семко Т.В. Імовірнісний аналіз діяльності будівельного підприємства / Т.В. Семко // Регіональні перспективи. – 2001. – № 5-6 (18-19). – С. 250-251.

3. Замков О.О. Математические методы в экономике: Учебник / О.О. Замков, А.В. Толстопятенко, Ю.Н. Черемных / Под общ. ред. д.э.н., проф. А.В. Сидоровича; МГУ им. М.В. Ломоносова. – 3-е изд., перераб. – М.: Издательство «Дело и Сервис», 2001. – 368с.