Шилинец В. А., Двуреченская М. Г., Ольшевская А. В.

Белорусский государственный педагогический университет

РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ МЕТОДОМ МОНОГЕННЫХ В СМЫСЛЕ В.С. ФЕДОРОВА ФУНКЦЫЙ

Для исследования дифференциальных уравнений в частных производных используются разные методы. Одним из таких методов является метод функций, моногенных в смысле В.С. Федорова (F-моногенных) [1–9]. В частности, при помощи F-моногенных функций удается построить функционально-инвариантные решения системы Максвелла для электромагнитного поля в пустоте [10]. Кроме этого, при помощи указанных функций удается для отдельных видов дифференциальных уравнений и систем дифференциальных уравнений строить решения в замкнутой форме.

В данной работе при помощи F-моногенных функций исследуется система трех дифференциальных уравнений в частных производных с тримя неизвестными функциями и постоянными коэффициентами.

Рассмотрим систему дифференциальных уравнений в частных производных вида

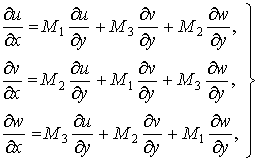(1)

где – искомые комплекснозначные функции двух действительных переменных ; – некоторые комплексные константы.

Для изучения указанной системы дифференциальных уравнений (1) используем линейную ассоциативно-коммутативную алгебру (гиперкомплексную систему) с единицей над полем комплексных чисел. Алгебра имеет базис , закон умножения определяется равенством .

Рассмотрим сначала задачу о приведении системы дифференциальных уравнений (1) к гиперкомплексному виду

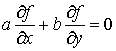, (2)

где , , , – комплексные константы.

Из системы (1) получаем

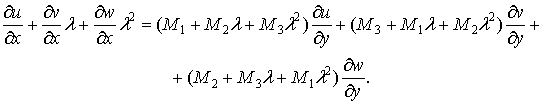(3)

Уравнение (3) можно рассматривать как условие (2) при в алгебре , где закон умножения определяется равенством .

Последнее уравнение (3) можно записать в следующем виде:

, (

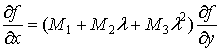где .

Как известно [1, 2], условие (необходимое и достаточное) моногенности одной гиперкомплексной функции по другой гиперкомплексной функции в некоторой области плоскости имеет вид

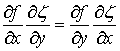
(причем предполагается, что в каждой точке области существует элемент данной алгебры , обратный значению или в этой точке).

Отсюда следует, что уравнение ( выражает моногенность гиперкомплексной функции по гиперкомплексной функции , где функция удовлетворяет следующим условиям:

,

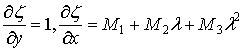откуда получаем, что

.

Таким образом, общим решением системы дифференциальных уравнений в частных производных (1), записанным в гиперкомплексном виде, в данной области плоскости будет произвольная гиперкомплексная функция

, моногенная в смысле В.С. Федорова в области по функции .

В этом случае условимся писать . Если исследовать структуру функций , то получаем следующую теорему.

Теорема. Общее решение системы дифференциальных уравнений в частных производных (1) имеет вид:

,

,

,

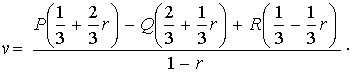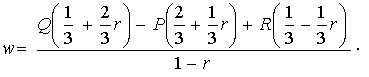где (, ) – произвольная комплексная функция,
F-моногенная в области по функции (, ); .

Литература:

1. Федоров В.С. Основные свойства обобщённых моногенных функций

// Известия вузов. Математика, 1958.– № 6.– С. 257-265.

2. Павлов С.Д. Решение систем линейных дифференциальных уравнений с частными производными с помощью моногенных функций в смысле
В.С. Федорова // Anal. stiint. Univ. Iasi, 1962. – T.8, f. 2.– P. 323-329.

3. Стельмашук Н.Т. О некоторых линейных дифференциальных системах в частных производных // Сибирский математический журнал, 1964.– Т.5, № 1.– С. 166-173.

4. Федоров В.С., Стельмашук Н.Т. Решение некоторых уравнений в частных производных методами F-моногенных функций // Rev. Roum. de Math. Pures et Appl., 1973. – Т. 18, № 2.– Р. 233-241.

5. Кусковский Л.Н. О краевой задаче типа Римана-Гильберта // Дифференциальные уравнения, 1975.– Т. 11, № 3.– С. 523-532.

6. Стельмашук Н.Т., Пенчанский С.Б. О решении одной линейной дифференциальной системы в частных производных методами F-моногенных функций // Дифференциальные уравнения, 1990.– Т. 26, № 4.– С. 724-727.

7. Стельмашук Н.Т., Шилинец В.А. Метод формальных производных для решения задачи Коши для одной системы дифференциальных уравнений в частных производных // Дифференциальные уравнения, 1993.– Т. 29, № 11. – С. 2019-2020.

8. Stelmashuk N.T., Shylinets V.A. The solution of the boundary value problem for a system of equations in formal derivatives by means dual differential operators // Труды института математики НАН Беларуси, 2004.– Т. 12, № 2.– С. 170-171.

9. Стельмашук Н.Т., Шилинец В.А. О преобразовании к каноническому виду системы линейных уравнений в частных производных с помощью двойных дифференциальных операторов // Весці НАН Беларусі. Сер. фіз.-мат. навук, 2008.– № 2.– С. 61-65.

10. Стельмашук Н.Т. Об одном исследовании системы Максвелла с помощью F-моногенных функций // Журнал вычислительной математики и математической физики, 1967.– Т. 7, № 2.– С. 431-436.