Математика/5.Математическое моделирование

К. ф.‑м. н. Карнаух Т.А.

КНУ им. Т. Шевченко, Украина

Метрики в пространствах моделей

Прикладная наука, в основном, оперирует конечноопределенными моделями объектов реального мира. При этом над моделями (представлениями) объектов реального мира выполняются действия (например, вычисления), моделирующие реальные действия, производимые над реальными объектами. Фундаментальной проблемой тут является то, что один и тот же объект (процесс, явление и т.д.) может иметь несколько синтаксически различных моделей, причем эти модели являются семантически эквивалентными, а потому результаты их обработки также должны быть семантически эквивалентными, то есть не зависеть от представления входного объекта. Назовем эту проблему проблемой постоянства результата.

Поэтому первый и наиболее естественный метод решения проблемы — требовать от модели вычислений, чтобы результаты обработки семантически эквивалентных представлений задавали один и тот же объект (были семантически эквивалентны). Данная задача отнюдь не является тривиальной.

Переход от произвольного входного представления к каноническому представителю класса семантически эквивалентных моделей и дальнейшие вычисления над каноническим представителем решают проблему постоянства результата лишь для узкого класса задач: во многих случаях проблема семантической эквивалентности является алгоритмически неразрешимой (например, не является алгоритмически разрешимой эквивалентность машин Тьюринга).

Несколько другой подход к решению обозначенной проблемы состоит в том, чтобы изначально ставить условие, чтобы на вход подавались только канонические представители, а вычисления над неканоническими представлениями не рассматривались.

Рассмотрим, что происходит в случае теории R‑преобразователей, предложенной Л.П. Лисовиком [1]. R‑преобразователь, моделируя (задавая) функцию действительного аргумента, производит вычисления над w‑словом — бесконечным двоичным представлением аргумента. Как известно, некоторые числа (не равные нулю двоично-десятичные) имеют два различных представления, например: 0.5 = (0.1(0))₂ = (0.0(1))₂. В теории R‑преобразователей им соответствуют w‑слова 0Ñ10^w и 0Ñ01^w (символ Ñ обозначает разделитель целой и дробной части). Первый подход к решению проблемы постоянства результата приводит к такому понятию как реал. Результат последнего подхода — определение функции, заданной R‑преобразователем (представления вида w1^w в качестве входа не рассматриваются).

Итак, в большинстве пространств моделей синтаксически различные объекты могут быть семантически эквивалентны. Во многих задачах необходимо оценивать расстояние между объектами и соответствующие пространства реальных объектов являются метрическими. Рассмотрим, что происходит при переносе метрики из реального пространства в пространство моделей объектов реального пространства.

Естественно требовать, чтобы синтаксически близкие представления (модели) были семантически близки. Пусть задано метрическое пространство (X, d_X) реальных объектов, пространство моделей M и сюръективное отображение n:M®X, по модели восстанавливающее объект. Расстояние d_S между моделями можно определить как семантическое расстояние, то есть как расстояние между объектами, которые представляют модели:

"m₁, m₂ÎM d_S(m₁, m₂) = d_X(n(m₁), n(m₂)).

В пространстве M функция d_S удовлетворяет аксиоме симметрии и неравенству треугольника, однако первая аксиома метрики для нее может не выполняться: различные представления в силу семантической эквивалентности оказываются на нулевом расстоянии. Таким образом, d_S метрикой не является.

Такой подход к расстоянию между представлениями используется, в частности, в теории R‑преобразователей, где расстояние между представлениями действительных чисел определяется как расстояние между самими действительными числами и, по сути, метрикой не является. Именно этот факт приводит к появлению понятия частично непрерывной функции [1].

В связи с этим интересным представляется исследование того, какая теория буде получена при ослаблении первой аксиомы метрики

"x, yÎX ((d(x, y) = 0) ~ (x = y) )

до такой

"xÎX d(x, x) = 0.

Отображение d:X´X®[0;+¥), удовлетворяющее условиям:

"xÎX d(x, x) = 0 (аксиома равенства),

"x, yÎX d(x, y) = d(y, x) (аксиома симметрии),

"x, y, zÎX d(x, y) + d(y, z) £ d(x, z) (неравенство треугольника),

будем называть псевдометрикой пространства X, а саму пару (X, d) — псевдометрическим пространством.

В случае пространств моделей уместно различать синтаксическое и семантическое расстояние. Более того, в качестве семантического расстояния можно использовать псевдометрику d_S, увязывая ее с метрикой d, задающей синтаксическое расстояние. Как указывалось ранее, синтаксически близкие объекты должны быть близки семантически, поэтому для пары (d_S, d) уместно требовать выполнение ограничения

"x, yÎX d_S(x, y) £ f(d(x, y)),

где функция согласования f:[0; +¥)®[0; +¥) непрерывна в некоторой окрестности нуля, причем f(0) = 0.

В случае существования такой функции f расстояния d_S и d будем называть согласованными.

Пусть a = a₁a₂…, b = b₁b₂… — элементы пространства S = {0, 1}^w. Пусть

d(a, b) = 1/n, где n таково, что a_n ¹ b_n и a₁a₂…a_n‑1 = b₁b₂…b_n‑1, если a ¹ b;

d(a, b) = 0, если a = b;

d_S(a, b) = | ||a||-||b|| |, где ||c₁c₂…|| = .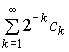

Тогда для пространства S функция d является метрикой, а d_S — псевдометрикой. В качестве функции согласования можно рассмотреть f(x) = x.

Псевдометрики и согласованные расстояния могут использоваться в задачах распознавания. При распознавании чаще всего приходится отождествлять некоторые вариации представления распознаваемого объекта, а потому фактически используется псевдометрика. Кроме того, задачу распознавания можно формулировать как задачу оценки расстояния между реальным объектом и объектом, задаваемым моделью, в пространстве реальных объектов. А эта задача плавно переходит в задачу проверки соответствия модели испытуемого объекта модели образца. (Например, можно ставить задачу определения идентичности (близости) двух объектов по алгоритмам их распознавания/вычисления.) А для таких задач полезны согласованные расстояния d_S и d. Для определенных классов алгоритмических моделей синтаксическое расстояние d оценить намного проще, чем семантическое. (В рассмотренном примере с пространством S для различных элементов синтаксическое расстояние является вычислимым за конечное время.) А тогда по оценке синтаксического расстояния можно делать выводы о семантической близости и таким образом решать задачу распознавания.

Литература:

1. Лисовик Л. П. Логические свойства частично непрерывных функций. // Тр. ин-та математики СО АН СССР. – Математическая логика и алгоритмические проблемы. Н.: Наука, 1989. – Т. 12. – С. 39-72.