УДК
519.71
Математика/5.
Математическое моделирование
к.ф.-м.н. Копытова О.М.
Донецкий национальный технический
университет, Украина
О возможности сохранения
поведения автомата
при перебросках дуг
Введение
Сложные системы, взаимодействующие со средой, могут подвергаться деформирующим воздействиям с её
стороны, вследствие чего может изменяться их поведение. В связи с этим
возникают задачи анализа поведения систем, которые подверглись таким искажающим
воздействиям. Одной
из основных математических
моделей систем является модель конечного автомата. Вышеуказанные задачи
анализа поведения в рамках автоматной модели изучаются в теории экспериментов с
автоматами, технической диагностике, теории синтеза дискретных систем, где они
являются ключевыми. В частности эти вопросы становятся всё более актуальными в
связи с широким внедрением различных микроэлектронных систем и компонент
критического применения и повышенными требованиями к достижению необходимого
уровня безопасности [1].
В ряде случаев автоматы, структура которых подверглась искажениям, могут
быть устойчивыми к ним, сохраняя своё поведение неизменным. В настоящей работе
продолжается исследование поведения автоматов Мили, когда в качестве
искажающего воздействия выступает операция переброски дуг в графе переходов автомата.
Известно [2], что в результате переброски
ровно одной дуги в приведенном автомате или при изменении её выходной отметки
получается автомат, не изоморфный исходному. В [3] были сформулированы достаточные условия сохранения
поведения автоматом при переброске двух дуг, и было показано, что для любого
натурального k > 1 существует приведенный автомат, в котором найдется
подмножество из k дуг, одновременная переброска которых приводит к изоморфному
автомату.
В настоящей работе основное внимание уделено получению необходимых
условий, при которых переброска двух дуг приводит к автомату, эквивалентному
исходному.
1. Формальная постановка задачи
Основные определения теории
автоматов можно найти, например, в [4].
Под
автоматом будем понимать автомат Мили A=(A, X, Y, d, l ), где A,
X, Y - алфавиты состояний, входов и выходов соответственно, а d, l − функции
переходов и выходов. Как обычно, будем обозначать автомат символом множества
его состояний. Автомат A будем
рассматривать также как множество дуг ЕА,
где дуга − это четверка (s,x,y,t), если d(s,x) = t, l(s,x) = y. Функции d и l обычным
образом распространяются на множество X* всех входных слов конечной длины.
Два
состояния a и b одного и того же
автомата A или двух разных автоматов,
соответственно A и B, называются эквивалентными, если для
всякого входного слова рÎX* выполняется l (а, р) = l' (b, р), где l' - функция выходов автомата A или B. Автомат
называется приведенным, если все его состояния попарно неэквивалентны.
В
дальнейшем будем рассматривать автоматы A
и В, у которых входные и выходные
алфавиты совпадают, то есть A = (A, X, Y,
d, l ) и B = (B, X, Y, d', l'). Как
обычно, отображение φ: A → B
будет называться изоморфизмом автомата A
на автомат B, если для любых aÎ A и xÎ X :
1) φ(d(а, х)) = d (φ(а), х);
2) l(а, х) = l'(φ(а), х),
причём для любой
дуги е' =(a', x, y , b') автомата В найдётся
такая дуга е =(a, x, y, b) автомата А, что
е' =(φ(a), x, y, φ(b)). В этом случае автоматы А и В называем изоморфными и обозначаем А = В.
Пусть
A =(A, X, Y, d, l ) − приведенный автомат и е=(s, x', y', s1) − его дуга.
Под переброской дуги е, например, в состояние s2 будем понимать замену этой дуги на дугу(s, x', y', s2). Далее, если не оговорено
противное, рассматриваются переброски, при которых s1≠s2. Пусть
автомат А' получен из автомата А переброской некоторого множества дуг М Í ЕА. Задача заключается в том, чтобы определить условия,
при которых автомат А'
остается изоморфным исходному автомату
A.
Пример сохранения поведения. Легко привести примеры, когда результатом переброски
в автомате двух дуг является новый автомат, не изоморфный исходному.
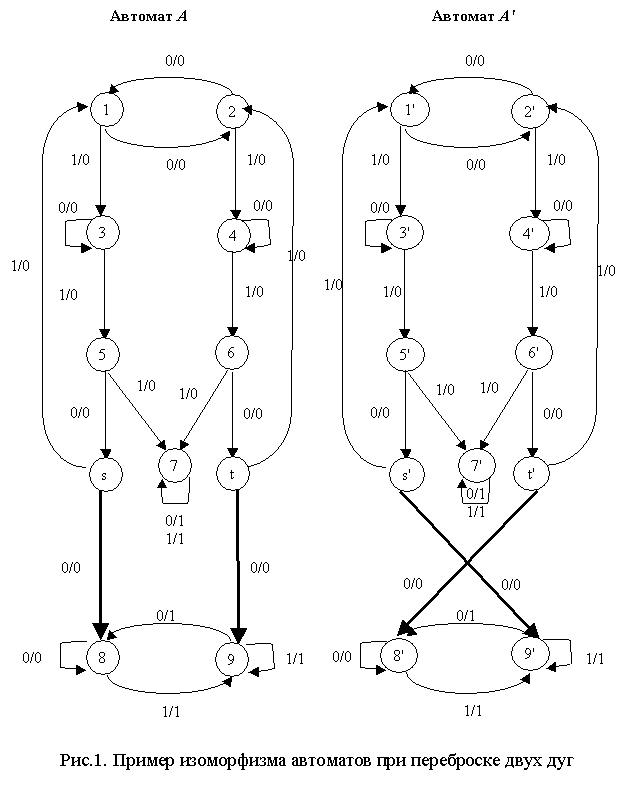
Рассмотрим
противоположный пример, когда переброска двух дуг в приведенном автомате
приводит к автомату, изоморфному заданному(см. рис.1). Автомат А' является результатом переброски двух
дуг в автомате А: дуга(s, 0, 0, 8) перебрасывается в состояние 9, т.е. заменяется дугой(s, 0, 0, 9), а дуга(t, 0, 0, 9) перебрасывается в состояние 8, т.е. заменяется дугой(t,
0, 0, 8). Легко видеть, что отображение
φ : A → А', такое, что: φ(1) = 2; φ(2) = l;
φ(3) = 4;
φ(4) = 3;
φ(5) = 6;
φ(6) = 5;
φ(7) = 7; φ(s) = t;
φ(t) = s; φ(8) = 8; φ(9) = 9, реализует изоморфизм автомата A на автомат А', т.е. автомат А' также
приведен и эквивалентен автомату A.
2. Необходимые условия сохранения
поведения при переброске двух дуг
Пусть
автомат А' является результатом
переброски некоторых двух различных дуг в автомате A. Пусть, например, в автомате
А' дуга(s, x', y', s1) заменена
дугой(s, x', y', s2), а дуга (t,
x'', y'', t1) заменена дугой(t, x'', y'', t2).
Состояния
a
и b автомата A
называются k-эквивалентными
[4], если для всякого входного слова р длины k выполняется
равенство l(а, р) = l(b, р). Обозначим
через εk отношение k-эквивалентности на
множестве состояний А. Обозначим класс k-эквивалентности, содержащий некоторые состояния u, v, … через εk(u,v, …). Отношение
эквивалентности обозначим через ε. Если
l(а, р) ≠ l(b, р) для
некоторого входного слова
р, то говорят, что слово

р различает состояния a и b. Если k − минимальная
длина слова р, для которого l(а, р) ≠ l(b, р), то
состояния a и b автомата
A называются k-различимыми.
Состояния
автомата А'
будем помечать штрихом, а
обозначения для функций переходов и выходов оставим без изменения. Одноименные состояния автоматов А' и А вида (r, r') назовем двойственными состояниями. Пусть А' и А изоморфны и n − множество состояний автомата А.
При доказательстве последующих
утверждений будем пользоваться приёмом построения Рk-таблиц [2] для автомата В = А È А', полученного
приписыванием автомата А' к автомату
А.
Лемма 1. Состояния s и t 1-эквивалентны.
Доказательство. Предположим противное.
Построим Рk-таблицы
для автомата В=АÈА' и рассмотрим как с ростом k = 1, 2, … распадаются классы k-эквивалентности, содержащие s и
t. Заметим,
что в силу изоморфизма А' и
А, каждый класс в Рk-таблицах должен содержать
чётное число состояний − одинаковое число штрихованных и нештрихованных
состояний.
Так как значения функций выходов автоматов А
и А' одинаковы, то в таблице Р1 каждый класс эквивалентности
состоит из пар двойственный состояний. Отсюда следует, что (s, s') Î P1, (t , t') Î P1, но в силу исходного предположения, (s, t) Ï P1. Из
правил построения Рk-таблиц следует, что с ростом k каждый класс в таблице Рk
будет состоять из пар двойственный состояний до тех пор, пока не
распадётся хотя бы одна из пар (s, s') или (t, t'). Так как
А приведен, то найдутся такие i и j, что (s1, s2)Î Pi-1, но (s1, s2) Ï Pi и (t1, t2)Î Pj-1, но (t1, t2) Ï Pj, где
1 £ i £ n - 1, 1 £ j £ n - 1. При
этом возможно, что i = j.
Выберем
l = min(i, j). Пусть для определённости
l = i. Тогда
в Pi все классы, по-прежнему, состоят из пар вида(r, r'). При этом (s1, s1') Î Pi, (t1, t1') Î Pi,, но(s1, s2) Ï Pi. Из построения Рk-таблиц следует, что(s, s') Ï Pi+1, а класс состояний, эквивалентных состоянию s, содержит
само s и, возможно, пары вида(r, r'). Следовательно,
этот класс содержит нечётное число состояний, откуда следует, что А
и А' не изоморфны. Полученное противоречие доказывает лемму.
Из леммы 1 вытекает
Следствие 1. В автомате с двумя состояниями невозможно выполнить 2
переброски так, чтобы полученный автомат был изоморфен исходному.
Это следует из того, что
при n = 2
состояния s и t не являются 1-эквивалентными.
Лемма 2. (s, s') Ï ε,(t, t') Ï ε.
Доказательство. При доказательстве
леммы 1 было показано, что существуют такие i и j, что (s1, s2)Î Pi-1, но (s1, s2) Ï Pi и (t1, t2)Î Pj-1, но (t1, t2) Ï Pj, где
1 £ i £ n - 1, 1 £ j £ n - 1. Отсюда (s, s') Ï εi+1 и (t, t') Ï εj+1, и значит, (s, s') Ï ε и (t, t') Ï ε.
Лемма 3. Для автомата В = А È А' существует минимальное k > 1 такое,
что (s, s', t, t') Î εk-1, (s, t) Ï εk, (s, t') Î εk,, (s', t) Î εk и для всех
состояний r ≠ s, t справедливо (r, r')Î εk.
Доказательство. Из леммы 2 следует, что
существует минимальное k1 такое, что(s, s') Ï εk1 или (t, t') Ï εk1 или одновременно (s, s') Ï εk1 и (t, t') Ï εk1. Заметим, что в таблице Pk1 все состояния, кроме
s или t или
их обоих, входят в классы эквивалентности двойственными парами вида (r, r'). С другой стороны, в силу
приведенности автомата А, существует минимальное k2, при котором (s, t)Ï εk2. Покажем, что
k1 = k2 .
Предположим,
что k1 ≠ k2. Рассмотрим два возможных случая:
1.
k2 < k1. Тогда
εk2 (s, s')
≠ εk2 (t, t'), причём в таблице
Pk2 все классы состоят из пар двойственных состояний.
Отсюда следует, что в таблице Pk1 один
из классов εk1 (s) или εk1 (t) либо оба эти класса содержат нечётное число состояний. Но тогда автоматы А
и А' не изоморфны.
2. k1 < k2. Пусть
для определённости (s, s')Ï εk1. Возможны следующие два
случая:
a)
(t, t') Î εk1. Тогда
в таблице Pk1 все состояния, кроме s и s' , входят в классы k1-эквивалентности вместе со своими двойственными. Но тогда класс εk1 (s) , равно как и класс εk1 (s'), содержат
нечётное число состояний, откуда следует, что
А и А' не изоморфны;
b)
(t, t') Ï εk1. Поскольку
k1 < k2, то (s,t) Î εk1. Тогда
в таблице Pk1 состояния s' и t' не входят в класс εk1 (s,t) . При этом все остальные состояния,
отличные от s и t, входят в
классы таблицы Pk1 двойственными парами. Отсюда
следует, что класс εk1 (s,t) содержит
нештрихованных состояний больше, чем штрихованных. Следовательно, А и А' не изоморфны.
Полученное
противоречие доказывает, что k1 = k2. Другими словами, следующие пары состояний: (s, t), (s, s'), (t, t') являются k-различимыми,
где k = k1 = k2. Нетрудно видеть, что единственный способ разбиения класса εk-1 (s, s' , t, t') следующий: (s, t') Î εk, и
(s', t) Î εk . Лемма доказана.
Теорема 1. Справедливы
следующие утверждения:
1)
на перебрасываемых дугах
отметки входных символов совпадают: x' =
x'' , причём x' есть начальная буква
кратчайшего слова, различающего s и t;
2)
на перебрасываемых дугах
отметки выходных символов совпадают: y'= y'';
3)
состояния s
и t, из которых перебрасываются дуги, различны.
Доказательство. Докажем утверждение 1). По лемме 3 существует
минимальное k такое, что класс
εk-1 (s, s' , t, t' ) в таблице Pk разбивается на два класса: εk (s, t') ≠ εk (t, s'). Пусть p = x1 x2 … xk − слово минимальной длины k, различающее
s и
t.
Обозначим u = d ( s , x1) и v = d ( t, x1). Так как
x1 − начальная буква кратчайшего слова, различающего s и t, то (u, v) Ï εk-1. Покажем, что x1 = x' =
x''.
Предположим противное. Возможны
два случая: 1) x1 ≠
x', x'' и 2) x1= x'
≠ x'' либо
x1= x''
≠ x'. Рассмотрим
каждый из них.
Пусть x1 ≠ x',
x'' . В силу по леммы 3 для всех i<k в таблице Pi любой
класс состоит из пар вида(r, r'), Поэтому (u, u') Î εk-1, (v, v') Î εk-1. Учитывая, что(u, v) Ï εk-1, получаем
: (u, v') Ï εk-1. Но тогда (s, t') Ï εk, что противоречит лемме 3.
Пусть
теперь x1 = x'
≠ x'' или x1 = x''
≠ x'. Предположим
для определённости, что x1 = x'
≠ x''. Тогда u = d ( s , x1) =d ( s , x' ) =s1. По
лемме 3 (s, t) Î εk-1, но (s, t) Ï εk. По вышесказанному
(u, v) Ï εk-1 , т.е.
(s1, v) Ï εk-1. При этом (s1, v) Î εk-2 , так как в противном случае
состояния s и t были
бы (k - 1)-различимы.
Из леммы 3 следует, что (s1, s1', v, v' ) Î εk-2 и ( s1, s1' ) Î εk-1, (v, v' ) Î εk-1. Следовательно, (s1, v' ) Ï εk-1. Но тогда (s, t' ) Ï εk, что противоречит лемме 3. Случай x1= x'' ≠
x' рассматривается аналогично.
Итак,
в обоих случаях пришли к противоречию. Следовательно, x1 = x' = x''.
Докажем утверждение 2). По лемме 1
l (s, x) = l (t, x) для
любого входного символа х. По
доказанному утверждению 1) x'= x''. Отсюда y' = l (s, x') = l (t, x') = y''.
Докажем утверждение 3). Из утверждений 1) и 2) следует, что
обе перебрасываемые дуги должны иметь одну и ту же вход-выходную отметку.
Поскольку из одного и того же состояния нельзя перебросить две различные дуги с
одинаковыми вход-выходными отметками, то утверждение 3) справедливо.
Теорема доказана.
Заключение
Полученные необходимые условия
сохранения автоматом поведения при перебросках дуг совместно с достаточными
условиями из [4] дают определённый инструментарий, позволяющий исследовать
поведение такого рода автоматов.
Условия допустимой переброски
для двух дуг могут быть расширены на
переброску 2k дуг в случае, когда множество М может быть разбито на
двухэлементные классы дуг, для каждого из которых независимо выполняются
найденные условия.
Список литературы
1. Малиновский М.Л.
Синтез безопасных автоматов с функциональной деградацией. Управляющие системы и
машины, 2010, №1, с. 84 − 91.
2. Грунский И. С.,
Копытова О. М. О структуре контрольного эксперимента для
определенно-диагностируемого автомата. Теория управляющих систем, Киев: Наукова думка, 1987, с. 40 − 54.
3. Копытова О.М. О
структуре автоматов, сохраняющих поведение при перебросках дуг. Труды VIII
Международной конференции "Дискретные модели в теории управляющих
систем". Москва: Макс-Пресс, 2009, с. 155 − 159.
4. Грунский И.С.,
Козловский В.А. Синтез и идентификация автоматов. Киев: Наукова думка, 2004.