Технические науки / 12. Автоматизированные системы управления на производстве

Кулик, А,Я., Кулик Я.А, Кулик О.А.

Вінницький національний технічний університет

Використання перетворень Уолша

під час підготовки даних до передавання

Як відомо, сучасна теорія зв’язку для аналізу процесів використовує систему синусоїдних та косинусоїдних функцій. Пояснюється це рядом причин. Одною з них являється простота отримання гармонічних коливань. Іншою не менш важливою причиною є те, що гармонійні сигнали проходять без перешкод через лінійні інваріантні в часі системи.

При гармонічних (синусоїдних, косинусоїдних) впливах ці коливання зберігають свою форму при проходженні їх через будь-яку лінійну систему. Вихідні коливання можуть відрізнятися при цьому від вхідних тільки по амплітуді і по фазі.

Разом з тим передавання дискретних сигналів показує перспективність використання функції Уолша. Аналогічно вищезгаданим, вона є ортогональною системою, а властивості ряду Фур’є повністю відповідають ряду, побудованому на цих функціях. В наш час вже активно розробляються багатоканальні системи на основі функцій Уолша.

Для нормованих функцій Уолша прийняте позначення wal(n,), де n – номер функції, а знаходиться в інтервалі 0 < < 1. Звичайно розглядається безліч функцій Уолша wal(n,) при n = 0, 1, ..., N – 1, де N = 2i, і = 1, 2, 3, ...

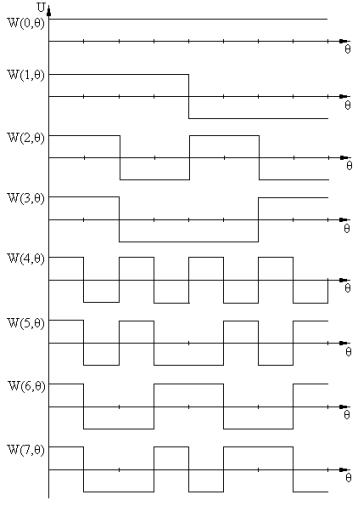
Перші вісім функцій Уолша зображені на рис. 1. Функції Уолша розрізняють за їх порядком і рангом. Під порядком мають на увазі максимальний з номерів розрядів, який вміщує одиницю, при двійковому представленні числа n, рангом називають кількість одиниць у двійковому поданні n. Наприклад, порядок і ранг функції wal(5,) дорівнюють відповідно 3 і 2, оскільки двійковим вираженням числа 5 є 101. Функції Уолша можуть бути представлені у вигляді добутку функцій Радемахера, виражених у двійковому коді Грея.

Для формування функцій Уолша може використовуватися і те, що добуток будь-яких двох функцій Уолша дає деяку іншу функцію Уолша. Якщо n_l — номер однієї з вихідних функцій і n₂— номер другої з них, то номер одержуваної при їхньому добутку функції визначається як n₁ n₂, тобто

wal(n_l,) wal(n₂,) = wal(n_ln₂, ).

Вказані функції можуть використовуватися не лише для спеціального аналізу, але й для апроксимації функцій, що дозволяє залучати їх для підготовки інформації, що має передаватися з метою стискання та захисту.

Засади побудови алгоритму полягають в тому, що на передавальному і приймальному боці інформація зберігається у вигляді комп’ютерних файлів, кожен з яких можна розглядати як таблично задану функцію та можна зчитувати з пам’яті комп’ютера у вигляді стандартного блока, довжина якого встановлюється в діалоговому режимі. Визначення номерів функцій Уолша, які апроксимують дану послідовність дискретних значень (байт) дозволяє передавати до каналу зв’язку не інформацію, а функції Уолша. На приймальному боці інформація може бути відновлена в повному обсязі [1].

Функція Уолша wal(j, J) визначається різницевим рівнянням

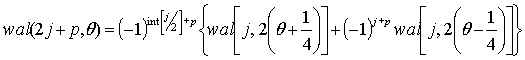. (1)

де 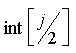використовується для найбільшого цілого числа, меншого чи рівного ;

p = 0 або 1;

j = 0,1,2,….;

wal(0;) = 1 для ;

wal(0;) = 0 для

Для пояснення цього різницевого рівняння доцільно розглянути функцію wal(j;). Функція wal(j; 2) має той самий вигляд, що і функція wal(j;), але стиснута до інтервалу . Функція wal[j;2(+1/4)] отримується зі зсувом wal(j;2) вліво на інтервал і wal[j;2(-1/4)] отримується зі зсувом wal(j;2) вправо на інтервал _.

В якості приклада можна розглянути випадок j = 0, p = 1 і j = 0, p = 1 .

Використовуючи значення [0/2] = 0 [2/2] = 1, можна отримати

wal(1,0) = (-1)⁰⁺¹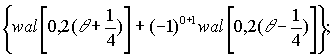

wal(5,0) = (-1)¹⁺¹ _.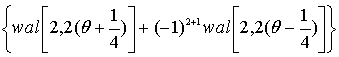

Добуток двох функцій Уолша дає іншу функцію Уолша: wal(h,) × wal(k,) = wal(r,). Це співвідношення може бути легко перевірено, якщо записати різницеве рівняння для wal(h,) та wal(k,) і помножити одне на одне. Виявляється, що добуток wal(h,) та wal(k,) задовольняє різницевому рівнянню виду (1).

Визначення значень r з різницевого рівняння трохи громіздке. Однак результат виходить простий: r дорівнює сумі h та r за модулем 2

wal(h,0) × wal(k,0) = wal(h k , ) (2)

Знак вказує на додавання за модулем 2. Система функцій Уолша, ортогональна і повна на всьому інтервалі , позначається де - дійсне число. З них можна визначити підклас функцій Уолша, знайомих як функції Радемахера:

cal(2k,) = cal(1,2k);

sal(2k,) = sal(1,2k); (3)

де k =

У двійковому вигляді

де дорівняє 1 або 0. Число називається двійково-раціональним, якщо сума має кінцеву кількість членів.

Функції cal(,) та sal(,) можливо визначити:

cal (,) =

sal(,) =

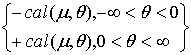
Наступні додаткові формули також важливі під час обчислень з функціями Уолша

wal(μ,) = wal (0,), 0 < < 1;

cal(μ,) = cal(0,), i

sal(μ,) = sal(0,), i – 1 < < i;

cal() = cal(μ,) × cal() ;

sal() = sal(μ,) × sal() .

Величина дорівнює половині середньої кількості змін знаків cal(μ,) та sal(μ,) на інтервалі часу довжиною 1.

В розглянутому випадку сходимість ряду буде вищою ніж для ряду Фур’є, оскільки для аналізу прямокутних сигналів в даному випадку використовуються не синусоподібні функції, а прямокутні ортогональні. Це означає, що для апроксимації вихідної послідовності необхідно значно менше членів рівняння і кінцевий обсяг даних буде меншим без втрат інформації. Також алгоритм оброблювання даних спрощується, тобто до каналу зв’язку необхідно передавати меншу кількість даних, за рахунок чого скорочується час передавання і підвищується ефективність використання каналу [2].

Певний нюанс полягає в тому, що до каналу зв’язку передається не сама інформація, а номери функцій Уолша, і без знання початкових умов і алгоритму перетворення відновити інформацію неможливо, тобто зберігається конфіденційність інформації.

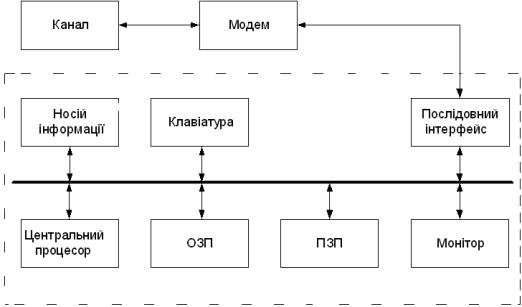
Рис. 1 – Схема реалізації способу кодування та передавання інформації

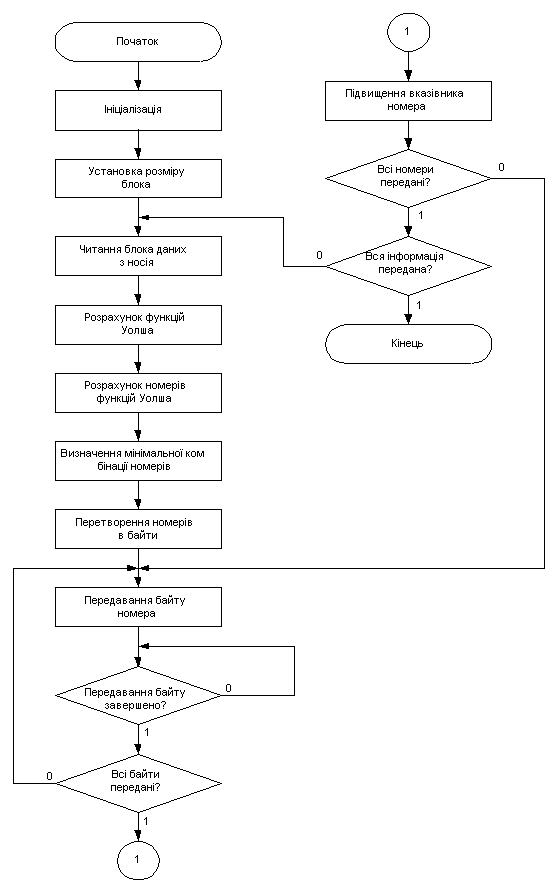
Рис. 2 – Схема програмного забезпечення для режиму передавання інформації

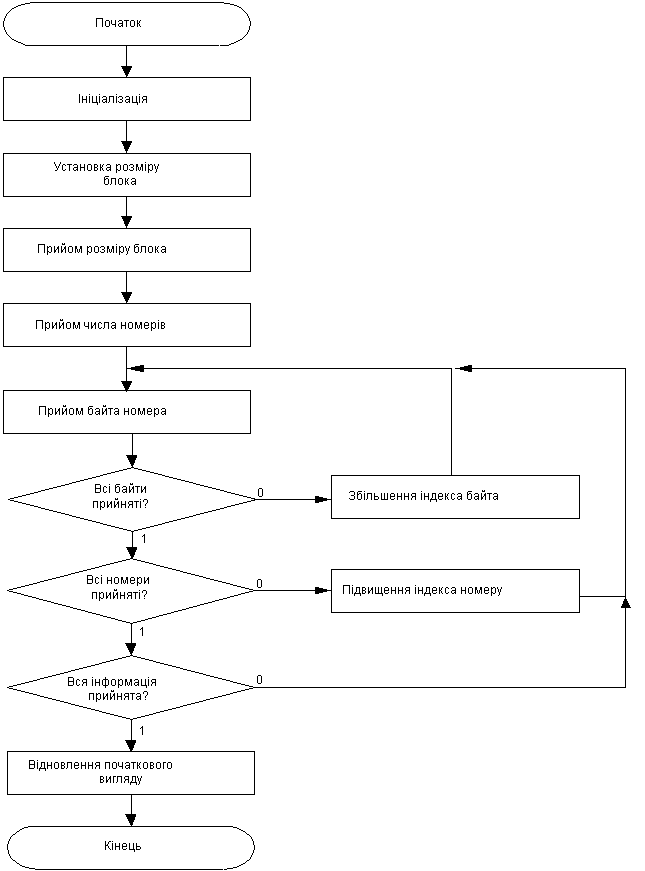
Рис. 3 - Схема програмного забезпечення для режиму приймання інформації.

Описаний алгоритм може бути реалізований за допомогою структурної схеми, наведеної вище.

Далі на рис. 2 подана схема програмного забезпечення для режиму передавання інформації; на рис. 3 – схема програмного забезпечення для режиму приймання інформації.

Відновлення блоку початкової інформації здійснюється за рахунок двійкового додавання функції Уолша з відповідними номерами.

Ефективність реалізації алгоритму буде найбільшою для передавання інформації саме в оптичному діапазоні, що набуває зараз широкого розповсюдження.

Література:

1. Х.Ф. Хармут. Передача информации ортогональными функциями. Пер. с англ. Дядунова Н.Г. и Сенина А.И. – М.: Связь, 1975.

2. Залманзон Л.А. Преобразование Фурье, Уолша, Хаара и их применение. – М: Связь, 1981.