Технические науки / 4. Транспорт

Неженцев А.Б.

Восточноукраинский национальный университет им. В. Даля

Устойчивость многомассовых моделей
мостовых кранов

Для исследования переходных процессов грузоподъемных кранов применяются многомассовые модели [1, 2 и др.], описываемые нелинейными дифференциальными уравнениями, которые интегрируются численными методами. При этом имеют место неустойчивые результаты численного интегрирования.

Цель работы: исследовать устойчивость (с помощью критерия Гурвица) трех- и четырехмассовой моделей, описывающих движение мостовых кранов:

- для трёхмассовой модели мостового крана

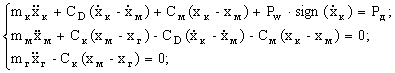(1)

- для четырехмассовой модели мостового крана

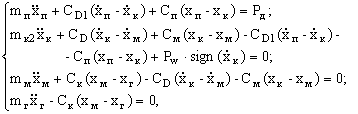(2)

где все обозначения общеприняты и приведены в работе [3].

После линеаризации приведенной к ходовым колесам силы привода и переобозначения переменных (, , , , , ) соответствующая системе (1) однородная система будет иметь вид:

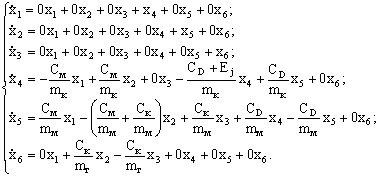(3)

Характеристическое уравнение для трёхмассовой модели:

(4)

Матрица Гурвица для трехмассовой модели имеет вид:

, (5)

где ; ; ; ; ;

; .

Определители Гурвица для трехмассовой модели:

; ; ;

.

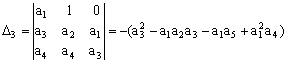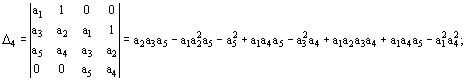
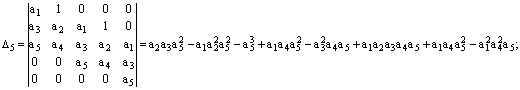
Поскольку коэффициенты системы уравнений (1) - положительные величины, то и определители Гурвица … также больше нуля. Но определитель равен нулю, что говорит о нахождении системы (1) на границе устойчивости и она не является асимптотически устойчивой, а - нейтрально устойчивой.

Также выполнен анализ устойчивости четырехмассовой модели мостового крана, для которой были получены аналогичные результаты.

Выводы:

- использование многомассовых моделей кранов без предварительной проверки на устойчивость может привести к ошибочным результатам исследований. Например, рассмотренные трёхмассовая и четырехмассовая модели, не являются асимптотически устойчивыми, а могут быть нейтрально устойчивыми, т.е. они могут применяться для исследования переходных процессов мостовых кранов только после проверки на устойчивость с определенными для каждого крана коэффициентами дифференциальных уравнений;

- увеличение числа масс в модели крана уменьшает запас ее устойчивости, поэтому модели, имеющие более пяти масс, как правило, неустойчивы при некоторых значениях коэффициентов уравнений. При увеличении числа масс в модели растет степень характеристического уравнения (для четырехмассовой модели – 8-я, для пятимассовой – 10-я) и - трудоемкость исследования модели на устойчивость;

- учет в многомассовых моделях механических характеристик электропривода крана на рабочих участках увеличивает запас устойчивости модели, поскольку двигатель в этом случае является демпфером колебаний, а на нерабочих участках (например, в начале разгона по естественной характеристике) - уменьшает запас устойчивости.

Литература

1. Казак С.А. Динамика мостовых кранов. - М.: Машиностроение, 1968. - 332 с.

2. Лобов Н.А. Динамика грузоподъемных кранов. - М.: Машиностроение, 1987. - 160 c.

3. Будиков Л.Я., Нгуен Н.К., Неженцев А.Б. Исследование динамики грузоподъемных кранов // Вестник машиностроения, №4. - М.: Машиностроение, 1981, - с. 39-42.