УДК 629.45.01

 

Бозымбаев Болатжан – соискатель Казахский университет путей сообщения, Республика Казахстан, г. Алматы.

Амирханов Аскарбек Болатович – соискатель Казахский университет путей сообщения, Республика Казахстан, г. Алматы.

 

Анализ возмущений, действующих на экипаж со стороны пути

 

Вертикальные колебания подвижного состава, возникающие при движении экипажа по пути, представляют собой сложный процесс и зависят как от свойств колебательной системы, так и от вида возмущений, которые носят случайный характер. В настоящее время име­ется большое количество работ по исследованию вертикальных возмущений на подвижной состав со стороны пути [1].

Все возмущения можно условно разделить на две группы [2]. К первой группе относятся возмущения, связанные с геометрическими на неровностями на поверхности катания рельсов и бандажей колес. Ко второй группе – параметрические возмущения, которые обуслов­лены изменением упругих, диссипативных и инерционных характерис­тик пути по его длине. Совокупное действие всех этих возмущений может быть сведено к эквивалентной геометрической неровности η [3], которая рассматривалась как нормаль­ная стационарная, центрированная случайная функция координаты пути [4], характеризующаяся спектральной плотностью .

Определение характеристик возмущающих воздействий в рамках гипотезы эквивалентной геометрической неровности производят пу­тем измерения вертикальных перемещений или ускорений букс движущегося подвижного состава. Для удобства использования в расчетах вертикальных колебаний экипажей на ЭВМ функцию спектральной пло­тности эквивалентной геометрической неровности , по­лученную по экспериментальным данным, аппроксимируют аналитическим выражением. Переход к аналитическому выражению широко испо­льзуется в ряде работ [5].

Так, в [6] уравнение монотонной составляющей функции спектральной плотности вертикальных перемещений букс тепловоза ТЭМ7 на прямых участках пути при скорости V=100 км/ч представлено в виде:

,                                                                                                (1)

где А=3,18∙10-4 м2, п=4,22 для стыкового пути.

Этот метод недостаточно точно описывает экспериментальную зависимость, поэтому в диссертации используется более точный метод аппроксимации функции спектральной плотности, разработанный профессором А.Н. Савоськиным [7].

Согласно этому методу аппроксимация осуществлялась аналитическим выражением, включающим совокупное влияние случайных изменений характеристик пути и круга катания колеса:

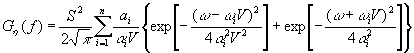,                            (2)

где S2 – дисперсия процесса;  ai – доля дисперсии i-той составляющей;

ωi – частота, соответствующая i-тому максимуму; αi – половина ширины i-того максимума функции , замеренная при ординате, соответствующей половине высоты этого максимума; V – скорость движения экипажа.

На рисунке 1 представлены зависимости функции спектральной плотности эквивалентной геометрической неровности, аппроксимированной выражением (2), по данным МИИТа (кривая I) и данным ВНИТИ-ЛТЗ (кривая 3). Параметры ai, αi и ωi, используемые в формуле (2) при V=1 м/с, приведены в таблице 1, где в числителе даны значения для  по данным ВНИТИ-ЛТЗ, а в знаменателе - по данным МИИТа.

Основная энергетическая часть спектра (93-94%) по форму­ле (2) приходится на две первые составляющие, представляю­щие собой первую и вторую гармоники стыковой неровности.

Второй способ задания возмущения в виде функции спектральной плотности эквивалентной геометрической неровности, который использован в диссертации, заимствован из [8], где предложено аппроксимировать спектральную плотность неровности для пути среднего состояния следующим аналитическим выражением, полученным на основе обработки статистических данных большого числа опытных поездок:

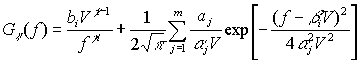,                                       (3)

 

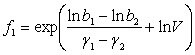,                                                                          (4)

 

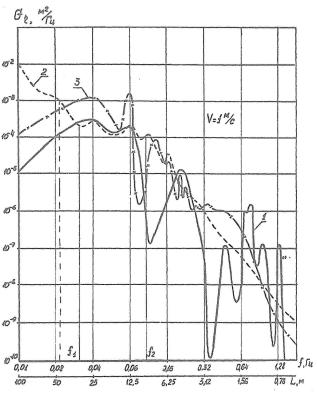
Рисунок 1 – Графики функции спектральной плотности возмущений

(1 – данные МИИТа, 2 – данные ВНИИЖТа, 3 – данные ВНИИЖТа-ЛТЗ)

Таблица 1 – Значения параметров

 

Номер составляющей спектра

ai

αi, рад/с:м/с

ωi, рад/с:м/с

S2, мм2

1

0,7400/0,55800

0,0750/0,05

0,251/0,247

54,1/25,5

2

0,1900/0,38400

0,0160/0,05

0,503/0,493

 

3

0,0530/0,04500

0,0500/0,12

0,867/1,315

 

4

0,0149/0,00372

0,0500/0,12

1,105/1,600

 

5

0,0500/0,00047

0,0628/0,15

1,344/3,165

 

6

0,0024/0,00329

0,0628/0,15

1,489/4,480

 

7

0,0008/0,00735

0,0628/0,15

1,784/5,097

 

8

0,0012/0,00153

0,0628/0,20

2,073/6,412

 

 

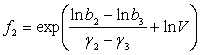,                                                                        (5)

i = 1 при f < f1,  i = 2 при f1≤ f < f2,  i = 3 при f ≥ f2,

где параметры, определяемые из условия достаточной точнос­ти аппроксимации экспериментальной кривой;

V – скорость движения;

I – частота.

Значения коэффициентов  приве­дены в таблице 2, а график функции спектральной плотности, соответствующий этим коэффициентам, показан в виде кривой 2 на рисунке 1.

 

Таблица 2 – Значения параметров

Параметры

Величины

Размерность

 

0,0055

9,9112

0,0125

 

-

 

3,1915

0,9892

4,1027

 

-

2,3816

2,2118

1,0591

0,4047

мм2

0,0424

0,0822

0,1216

0,1658

м-1

0,0031

0,0026

0,0052

0,0031

м-1

 

Вывод. Сопоставление графиков функций спектральной плотности верти­кальных неровностей возмущения (рисунок 1) показывает удовлет­ворительное совпадение результатов в диапазоне длин волн неров­ностей L=38–3,5 м. В то же время эти данные значительно разнятся при длинах волн неровностей > 38 м и < 3,5 м, что объясняется, по-видимому, разными методиками, используемыми при регистрации и обработке замеров эквивалентной геометрической неровности. В данной работе используются все три вида возмуще­ния, графики функций спектральной плотности которых представле­ны на рисунке 1. Значения зависимостей 1 и 3 определялись по фор­муле (2), а зависимости 2 - по формуле (3).

 

Литература

 

1. Камаев В. А. Оптимизация параметров ходовых частей железнодорожного подвижного состава. - М.: Машиностроение, 1980. - 215с. 

2. Динамическая модель пневморессоры рельсовых экипажей. / Савоськин А. Н., Бурчак Г. П., Гольдштейн И. А. Вестник ВНИИЖТа, 1983г., №8, с.33-45.

3. Колебания кузова локомотива на пневматических рессорах. / В. В. Филиппов, Савушкин. Вестник ВНИИЖТ, 1968 г. №8 с.34.

4. Львов А. А., Грачева Л. О. Современные методы исследования динамики вагонов. / Труды ЦНИИ МПС. Вып. 457. М.: Транспорт, 1972. 160с.

5. Бурчак Г. П., Савоськин А. Н., Сердобинцев Е. В. Прогнозирование надежности виброзащитных свойств рессорного подвешивания подвижного состава//Тр. МИИТ. 1976. вып.502. с.153-184.

6. Кудрявцев Н. Н., Белоусов В. П., Бурчак Г. П. Определение вертикальных возмущений, вызывающих колебания обрессоренных частей вагона при движении по рельсовому пути // Вестник ВНИИЖТ. - 1982. №5. с.33-37. Кудрявцев Н. Н., Белоусов В. П., Бурчак Г. П. Определение вертикальных возмущений, вызывающих колебания обрессоренных частей вагона при движении по рельсовому пути // Вестник ВНИИЖТ. - 1982. №5. с.33-37.

7. Савоськин А. Н. О выборе аналитического выражения для функции спектральной плотности случайных колебательных процессов // Тр. МИИТ.-1971. вып. 373. с.78-85.

8. Захаров А. Н. Вертикальные колебания вагонов электропоездов // Вестник ВНИИЖТ. -1982. №2. с.41-43.