Мельник В.Н. Карачун В.В.
Национальный технический университет Украины «КПИ»
КОЛЕБАНИЯ ПОРИСТОЙ ПЛАСТИНы В ЗОНЕ АКУСТИЧЕСКОЙ ТЕНИ
Анализ показывает,
что дополнительная масса в виде слагаемого ![]() при обычных параметрах пористой пластины не
оказывает существенного влияния на ее динамику. Кроме того, выяснилось, что
при обычных параметрах пористой пластины не
оказывает существенного влияния на ее динамику. Кроме того, выяснилось, что ![]() >>
>>![]() и
и
![]() >>
>>![]() .
.
Наибольший интерес
представляют изгибные колебания теневой стороны пластины. Положим для
конкретности, что ![]() м
м ![]() ,
, ![]() ,
, ![]() ,
, ![]() и проведем оценку колебаний пластины в
пространстве.
и проведем оценку колебаний пластины в
пространстве.
Выясним, прежде
всего, степень влияния угла падения![]() на характер вынужденного движения пластины. Как и в случае металлической
пластины, изменение длины изгибной волны сложным образом зависит от частоты
падающей волны
на характер вынужденного движения пластины. Как и в случае металлической
пластины, изменение длины изгибной волны сложным образом зависит от частоты
падающей волны ![]() .
.
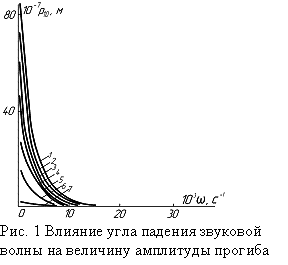 Что касается амплитуды колебаний,
то она убывает с ростом
Что касается амплитуды колебаний,
то она убывает с ростом ![]() ,
вообще говоря, по экспоненциальному закону и, в то же время, уменьшается по
абсолютной величине с увеличением угла
,
вообще говоря, по экспоненциальному закону и, в то же время, уменьшается по
абсолютной величине с увеличением угла ![]() (рис. 1). здесь кривая «І» соответствует углу
(рис. 1). здесь кривая «І» соответствует углу ![]() рад,
2 –
рад,
2 – ![]() рад,
3 – 0,591 рад, 4 – 0,784 рад, 5 – 0,985, 6 – 1,178 рад, 7 – 1,374 рад.
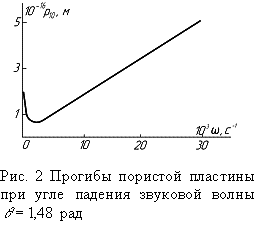
Диаграмма на рис. 2, соответствующая углу
рад,
3 – 0,591 рад, 4 – 0,784 рад, 5 – 0,985, 6 – 1,178 рад, 7 – 1,374 рад.
Диаграмма на рис. 2, соответствующая углу ![]() рад,
резко отличается от остальных графиков и выявляет уменьшение амплитуд до значений
частот
рад,
резко отличается от остальных графиков и выявляет уменьшение амплитуд до значений
частот ![]() с-1, а затем систематическое ее
увеличение до величины 6,5
с-1, а затем систематическое ее
увеличение до величины 6,5![]() .
Объективности ради, надо констатировать, что в абсолютных величинах эти
значения намного меньше, по сравнению с другими углами падения звуковой волны.
.
Объективности ради, надо констатировать, что в абсолютных величинах эти
значения намного меньше, по сравнению с другими углами падения звуковой волны.
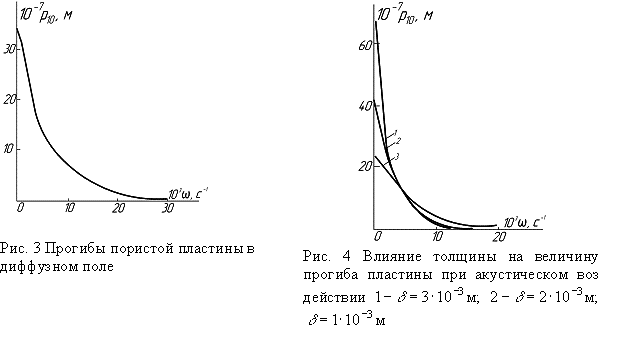
 В случае диффузного поля,
амплитуда изгибных колебаний пластины с увеличением угла
В случае диффузного поля,
амплитуда изгибных колебаний пластины с увеличением угла ![]() уменьшается по экспоненциальному закону с
ростом частоты
уменьшается по экспоненциальному закону с
ростом частоты ![]() (рис. 3).
(рис. 3).
Увеличение толщины
пластины приводит к росту абсолютной величины амплитуды изгибных колебаний.
Частотная характеристика принимает вид затухающей экспоненты (рис. 4).
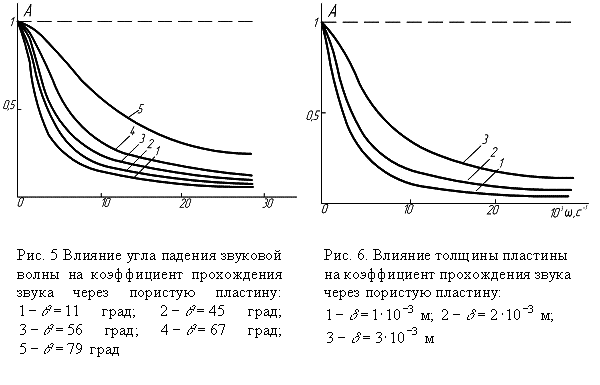
Не лишена интереса
оценка степени влияния угла падения звуковой волны на коэффициент прохождения
звука ![]() (рис. 5), а также влияние толщины пластины на
величину этого параметра (рис. 6). Численный анализ проведем в соответствии с
формулой –
(рис. 5), а также влияние толщины пластины на
величину этого параметра (рис. 6). Численный анализ проведем в соответствии с
формулой –
![]() .
.
Как видно, с
увеличением угла ![]() коэффициент прохождения звука уменьшается,
что имеет очевидную физическую сущность (рис. 5, рис. 6).
коэффициент прохождения звука уменьшается,
что имеет очевидную физическую сущность (рис. 5, рис. 6).
В действительности
акустическое воздействие носит, как правило, диффузный характер. Поэтому
осуществив осреднение по Пэрису, можно обобщить рассматриваемую расчетную
модель на равновероятный перенос энергии звуковой волны по углу ![]() .
.