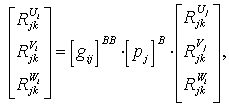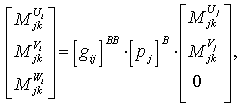Нурахметов Б.К., д.т.н Алматинский технологический
университет
Сартаев К.З. д.т.н Алматинский технологический университет
Бижанова А.С. Казахская академия транспорта и коммуникации
КИНЕТОСТАТИЧЕСКИЙ АНАЛИЗ ПАРАЛЛЕЛЬНОГО МАНИПУЛЯТОРА СО
СЛОЖНОЙ ПЛАТФОРМОЙ
Параллельный манипулятор со сложной платформой (рис. 1) предназначен для воспроизведения в абсолютной системе координат OXYZ семейства заданных дискретных положений точки Р рабочего органа
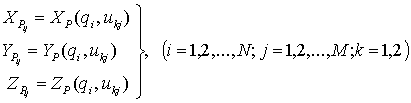 (1)
(1)
при N дискретных значениях обобщенной координаты
![]() (2)
(2)
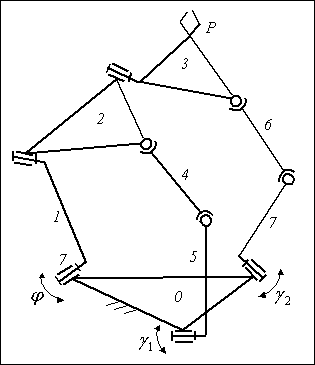
Рис.
1 Пространственный параллельный
манипулятор позиционирующего типа со сложной платформой
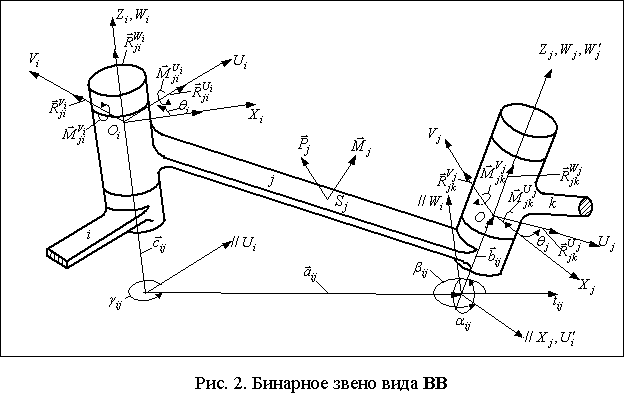
Для решения задачи кинетостатического анализа параллельного манипулятора со сложной платформой рассмотрим уравнения равновесия бинарных звеньев 2, 3, 4 и 6 вида ВВ, СВ, СВ, СС и СС (где В- вращательная и С- сферическая кинематические пары) соответственно.
Рассмотрим уравнения равновесия бинарного звена вида ВВ. С каждым элементом кинематических
пар ![]() и
и ![]() бинарного
звена
бинарного
звена ![]() вида ВВ (рис.2) жестко связываем системы
координат
вида ВВ (рис.2) жестко связываем системы
координат ![]() и
и ![]()
![]() .
.
Все внешние силы и
моменты, действующие на
звено ![]() , приводим в
точку приведения
, приводим в
точку приведения
![]() к главному вектору
к главному вектору ![]() и главному
моменту
и главному
моменту ![]() . Под действием
. Под действием
![]() и
и ![]() в кинематических парах
в кинематических парах ![]() и
и ![]() возникают силы
реакции.
возникают силы
реакции.
Силы реакции в
кинематических парах ![]() и
и ![]() , действующие на
звено
, действующие на
звено ![]() со стороны звеньев
со стороны звеньев
![]() и
и ![]() , приводим в точки
, приводим в точки ![]() и
и ![]() и заменим их главными векторами
и заменим их главными векторами ![]() и главными моментами
и главными моментами ![]() , которые в системах координат
, которые в системах координат ![]() и
и ![]() имеют
следующие компоненты
имеют
следующие компоненты
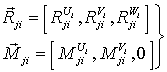 ,
, 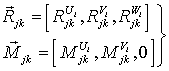 ; (4)
; (4)
Главные векторы ![]() и главные моменты
и главные моменты ![]() в системе координат
в системе координат
![]() имеют компоненты
имеют компоненты
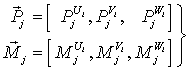 ,
, 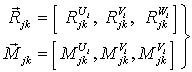 ; (5)
; (5)
Главный вектор
![]() и главный момент
и главный момент ![]() внешних сил, а также
силу и момент реакции
внешних сил, а также
силу и момент реакции ![]() и
и ![]() в кинематической паре
в кинематической паре
![]() приведем в
точку
приведем в
точку ![]() - начале систем координат
- начале систем координат ![]() и
и ![]() .
.
Тогда уравнения равновесия бинарного звена ![]() вида ВВ имеют вид
вида ВВ имеют вид
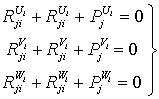 (6)
(6)
и
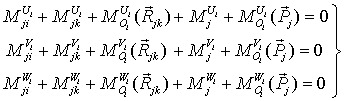 ,
(7)
,
(7)
где компоненты силы реакции ![]() и момента реакции
и момента реакции ![]() системах координат
системах координат
![]() и
и ![]() связаны между собой следующими матричными уравнениями
связаны между собой следующими матричными уравнениями
где ![]() и
и ![]() - подматрицы
вращений матрицы
- подматрицы
вращений матрицы ![]() бинарного звена вида ВВ
и матрицы
бинарного звена вида ВВ
и матрицы ![]() вращательной
кинематической пары.
вращательной
кинематической пары.
Подставляя
значения подматриц вращений ![]() и
и ![]() в уравнения (8),
получим
в уравнения (8),
получим
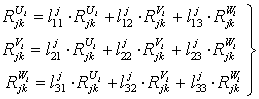 ,
, 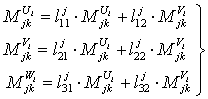 , (9)
, (9)
Тогда уравнения сил (6) бинарного звена ![]() принимают
вид
принимают
вид
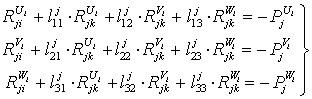 ; (10)
; (10)
В системе уравнений (7) величины ![]() и
и ![]() являются компонентами вектора момента силы реакции
являются компонентами вектора момента силы реакции ![]() относительно точки
относительно точки ![]() в системе
координат
в системе
координат ![]() , определяемого выражением
, определяемого выражением
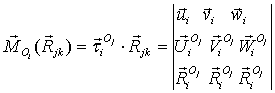 , (11)
, (11)
где ![]() - координаты точки приложения
- координаты точки приложения ![]() силы реакции
силы реакции ![]() в системе координат
в системе координат ![]() .
.
Кроме того, точка ![]() в системе координат
в системе координат ![]() имеет координаты
имеет координаты ![]() . Тогда между координатами точки
. Тогда между координатами точки ![]() в системах координат
в системах координат ![]() и
и ![]() существует связь в виде уравнения
существует связь в виде уравнения
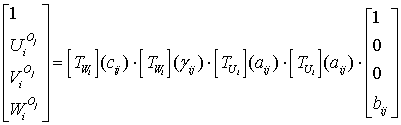 , (12)
, (12)
где ![]() и
и ![]() - матрицы
поступательных перемещений вдоль осей
- матрицы
поступательных перемещений вдоль осей ![]() на расстояния
на расстояния ![]() и матрицы поворотов
вокруг осей
и матрицы поворотов
вокруг осей ![]() на углы
на углы ![]() .
.
Подставляя в уравнение (12) матрицы переходов, получим
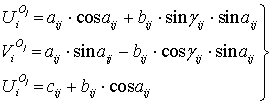 ; (13)
; (13)
Если подставить (12) в определитель (11) и раскрыть его относительно элементов первой строки, то получим
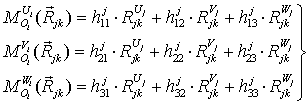 , (14)
, (14)
Подставляя компоненты моментов ![]() и
и ![]() из систем
уравнений (14) и (9) в систему
уравнений (7), получим окончательный вид уравнений моментов бинарного звена
из систем
уравнений (14) и (9) в систему
уравнений (7), получим окончательный вид уравнений моментов бинарного звена ![]() вида ВВ
вида ВВ
![]()
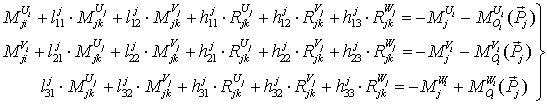 , (15)
, (15)
которые совместно с системой уравнений сил (10) составляют уравнения равновесия
бинарного звена ![]() вида ВВ.
вида ВВ.
Системы уравнений равновесия (10) и (15) преобразуем в матричные формы
![]() (16)
(16)
![]() (17)
(17)
где
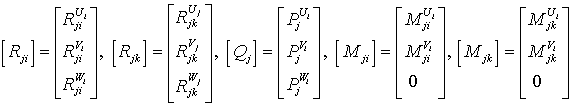 ,
,
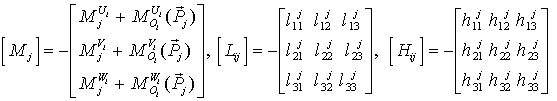 ;
;
Аналогично получаются уравнения равновесия бинарных звеньев вида ВС и СС.
Уравнения равновесия параллельного манипулятора со сложной платформой имеют вид
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
![]() (25)
(25)
![]() (26)
(26)
![]() . (27)
. (27)
Литературы
1. Zhumadil Zh. Baigunchekov, Scanderbek U. Joldasbekov, Modular Synthesis
of Spatial Manipulating Devices of High Classes, Proceedings of the Twelfth International Conference on CAD/CAM Robotics
and Factories of the Future, London, UK, 14-16 August 1996, pp. 685-690.
2. Zhumadil Zh. Baigunchekov,
Raj Gill, Anthony S. White, Nurlan Zh. Baigunchekov, The Basis of Structural
and Parametric Synthesis of The Parallel Manipulators with Functionally
Independent Drives (Part I and Part II), Proceedings
of The International Conference on Gearing, Transmissions and Mechanical
Systems. 3-6 July 2000, Nottingham Trent University, UK, (Additional Volume),
pp. 1-19.