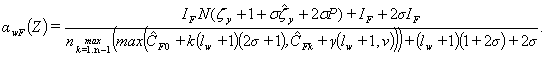Kryuchin O.V, Kryuchina E.I.
Tambov State University named after G.R. Derzhavin, Russia
The analytic model for parallel information processes training artificial neural networks with the full enumeration method usage
In papers [1-3] we have described the
information processes for the parallel weights searching with the full enumeration
method usage. In this article we want to analyze these processes and to develop
the analytic model for it.
As we know the number of
multiplicative operations which are executed by the serial full enumeration
algorithm can be calculated by formula
|
|
(1) |
where ![]() is the number of operations which are necessary for the serial inaccuracy
calculation (
is the number of operations which are necessary for the serial inaccuracy
calculation (![]() , here
, here ![]() ,
, ![]() are
are ![]() -th output values of the
simulating object and the model (ANN),
-th output values of the
simulating object and the model (ANN), ![]() is the pattern row number,
is the pattern row number, ![]() is the output vectors
is the output vectors ![]() and
and ![]() size),
size), ![]() is the algorithms iterations number (the information process
executes
is the algorithms iterations number (the information process
executes ![]() inaccuracy calculations and needs
inaccuracy calculations and needs ![]() operations for the cycle organization) [2].
operations for the cycle organization) [2].
For the count of multiplicative operations
which are executed by the information process of the full enumeration method it
is necessary to analyse all its steps. As we can see these are
1. the initialization;
2. passing data for the lead IR-element to other;
3. enumerating values of weights ![]() belonging the current IR-element;
belonging the current IR-element;
4. the data passing from all IR-elements to the lead;
5. selecting the optimal configuration by the lead IR-element.
In this algorithm we symbol the
element of information resource (for example a node of computer cluster) as “IR-element”.
In the frame of this element can be the computer cluster node or the calculation
network computer.
At the first step the lead IR-element
executes ![]() additive operations (it needs
additive operations (it needs ![]() operations for the cycle organization because ANN has
operations for the cycle organization because ANN has ![]() weights and
weights and ![]() operations for the values setting). At the second step it executes
operations for the values setting). At the second step it executes ![]() multiplicative and
multiplicative and ![]() additive operations. At this time other IR-elements execute
additive operations. At this time other IR-elements execute ![]() multiplicative and
multiplicative and ![]() additive operations, but it needs to wait the data sending by the
lead IR-element, thus each non-lead IR-element executes
additive operations, but it needs to wait the data sending by the
lead IR-element, thus each non-lead IR-element executes ![]() multiplicative operation.
multiplicative operation.
For reduction of addition operations to multiplication
operations the coefficient ![]() is used. This coefficient value is directly proportional to the
time spent for one addition operation and inversely related to the time spent
for one multiplication operation. So one multiplication operation needs the
time which is necessary for
is used. This coefficient value is directly proportional to the
time spent for one addition operation and inversely related to the time spent
for one multiplication operation. So one multiplication operation needs the
time which is necessary for ![]() addition operations and one addition operation can be changed to
addition operations and one addition operation can be changed to ![]() multiplication operations [4].
multiplication operations [4].
The number of executing operations at
the third step is alike to the number of operations which are executed by the serial
algorithm but the iterations number is ![]() for the lead IR-elements and is
for the lead IR-elements and is ![]() for other.
for other.
At the fourth step the lead IR-element
receives the best weight values and inaccuracy values for its from all non-lead
IR-elements that is why it executes ![]() multiplicative and
multiplicative and ![]() additive operations and non-lead IR-elements execute
additive operations and non-lead IR-elements execute ![]() multiplicative and
multiplicative and ![]() additive operations. After it the lead IR-elements needs to wait the
data sending.
additive operations. After it the lead IR-elements needs to wait the
data sending.
At the fifth step the lead
IR-element executes ![]() additive operations. We will convert additive operations values to
multiplicative and the result of it is shown at the table 1.
additive operations. We will convert additive operations values to
multiplicative and the result of it is shown at the table 1.
Table 1. The multiplicative operations numbers.
|
Step |
Lead IR-element |
Non-lead ( |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
Thus before receiving weights and inaccuracy
values by the lead IR-element it does three steps (it symbols the total
operations number as ![]() ), and other IR-elements do 4 steps (it
symbols the total operations number as
), and other IR-elements do 4 steps (it
symbols the total operations number as ![]() ). For the first two steps execution
the lead IR-element makes
). For the first two steps execution
the lead IR-element makes ![]() operations and the
operations and the![]() -th executes
-th executes ![]() operations.
operations.
And it is necessary to consider the
time of passing inaccuracy and weights. The receiving will end after sending the
inaccuracy by the slowest IR-element that is why the information process which
uses the parallel weights training needs ![]() operations. The
operations. The ![]() value can be calculated by formula
value can be calculated by formula
|
|
(2) |
So
the parallel information process efficiency can be
calculated by formula
|
|
(3) |
And the
analytic model is
defined by formula
|
|
(4) |
Bibliography
1.
Крючин О.В., Арзамасцев А.А., Королев
А.Н., Горбачев С.И., Семенов Н.О. Универсальный симулятор, базирующийся на
технологии искуственных нейронных сетей, способный работать на параллельных
машинах / О.В. Крючин [и др.] // Тамбов: Вестн. Тамб. ун-та. Сер. Естеств. и
техн. науки. 2008. – Т.13, Вып. 5. – C. 372-375.
2.
Крючин О.В. Параллельный алгоритм полного сканирования
обучения искусственных нейронных сетей // В мире научных открытий, Красноярск,
2010, №6.3 (12), C. 72-79.
3. Крючин, О.В. Параллельные
алгоритмы обучения искусственных нейронных сетей / О.В. Крючин // Матер. XV
междун. конф. по нейрокибернетике. Т. 2. Симпозиум «Интерфейс
''Мозг-Компьютер''», 3-й Симпозиум по Нейроинформатике и Нейрокомпьютерам. –
Ростов-н/Д. 2009. – C. 93-97.
4.
Oleg V.
Kryuchin, Alexander A. Arzamastev, Prof. Dr. Klaus G. Troitzsch (2011):
Comparing the efficiency of serial and parallel algorithms for training
artificial neural networks using computer clusters, Arbeitsberichte aus dem
Fachbereich Informatik, 13/2011, Universität Koblenz-Landau, ISSN (Online)
1864-0850. http://http://www.uni-koblenz.de/~fb4reports/2011/2011_13_Arbeitsberichte.pdf.