Математика/5. Математическое моделирование

Магистрант Жаксылыкова Г.А.

К.ф.-м.н., доцент Камалова Г.А.

Западно-Казахстанский аграрно-технический университет им.Жангир хана, Республика Казахстан

Имитационное моделирование, как средство решения задач систем массового обслуживания

Системы массового обслуживания являются одним из методов исследования сложных систем. Имитационная модель воспроизводит процесс функционирования реальной системы во времени.

Суть имитационного моделирования состоит в возможности исследования любых сложных систем, с учетом таких факторов и условий, которые трудно учитывать при аналитическом моделировании. Поэтому во многих случаях имитационное моделирование становится наиболее эффективным, а часто и практически единственно доступным методом исследования систем. Например, результативный анализ СМО типа G/G/N аналитическими методами невозможен, в то время как такой анализ методами имитационного моделирования не представляет особой сложности.[1]

При исследовании систем со стохастическим характером функционирования результаты, полученные при единичном выполнении имитационной модели, носят частный характер. Следовательно, для того, чтобы найти одну оценку какой-либо характеристики функционирования системы необходимо многократно использовать имитационную модель с последующей статистической обработкой полученных данных для наиболее эффективного решения поставленной задачи. Поэтому в имитационной модели должны быть предусмотрены средства сбора и средства последующей статистической обработки данных, полученных в ходе моделирования по интересующим характеристикам системы. Например, моделирование случайной величины Y, распределенной по экспоненциальному закону с параметром l, предполагает выполнение следующих действий:

1) розыгрыш равномерно распределенного случайного числа xÎ[0,w];

2) определение соответствующего значения .

Единичная реализация этой элементарной имитационной модели из двух действий дает одно значение случайной величины Y. Если цель моделирования состоит в оценке среднего значения , то необходимо добавить в модель дополнительное действие S = S + y для накопления суммы случайных величин и многократно реализовать полученную модель. В конце моделирования в качестве оценки для принять отношение S/N, где S/N – средство обработки, N – общее число реализаций модели.

Если необходимо построить функциональную зависимость среднего значения , например, от параметра l, то для множества точек этой зависимости нужно проделать каждый раз всю описанную выше процедуру моделирования, сбора и обработки данных. Даже в такой простой задаче очевидным образом проявляется присущий имитационному моделированию недостаток — это его трудоемкость.[2]

Процесс функционирования системы — это последовательная смена состояний системы во времени или другими словами, процесс функционирования системы — это переход ее из одного состояния в другое. Причина перехода системы из состояния в состояние называется событием, которое является, в свою очередь, следствием начала или окончания соответствующего действия.

Рассмотрим действия и события, имеющие место в системах на примере СМО типа G/G/1, где под состоянием системы понимается число заявок k, находящихся в ней в данный момент времени. Хронологическая последовательность действий и событий, имеющих место в такой СМО при прохождении через систему одной заявки, представлена на рисунке 1.

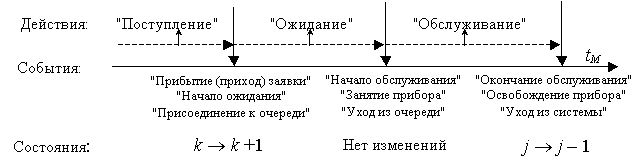
Рисунок 1. Прохождение одной заявки в системе массового обслуживания

Как видно из рисунка 1 не все события, возникающие в системе, являются равнозначными в том смысле, что не все события приводят к изменению состояния системы. Исходя из этого, различают два вида событий:

1) основные события;

2) вспомогательные события.

Основным событием называется событие, наступление которого приводит к изменению состояния системы. Именно основное событие имелось в виду при определении события как причины перехода системы из одного состояния в другое. Очень часто при имитационном моделировании дается другое определение основного события как события, время наступления которого можно планировать заранее, т.е. рассчитать его можно до фактического возникновения события.

Любое событие, не являющееся основным, называется вспомогательным. Вспомогательные события являются следствием возникновения основных событий и, следовательно, зависимы от них и наступают тогда же, когда и основные.

Для описания системы независимы и задаваемы независимые временные параметры, протекающие в ходе основных событий.

Для рассматриваемой нами системы G/G/1 такими параметрами являются интервалы поступления и длительности обслуживания заявок. Очевидно, что по истечении интервала поступления и длительности обслуживания наступают соответственно события "прибытие заявки" и "окончание обслуживания". Именно эти два события и являются основными в рассматриваемой системе, и появление их вызывает очевидные переходы системы из состояния в состояние. Все другие события (рисунок 1) являются вспомогательными. Так, события "начало обслуживания" и "занятие прибора" являются следствием наступления либо события "приход заявки" (если система свободна), либо события "окончание обслуживания" (для предыдущей заявки). В свою очередь, события "освобождение прибора" и "уход из системы" являются следствием возникновения события "окончание обслуживания". Ни одно вспомогательное событие, очевидно, не приводит к изменению состояния системы.[3]

Таким образом, процесс функционирования системы, будучи процессом перехода из состояния в состояние, можно представить как упорядоченную во времени последовательность основных событий, происходящих в системе и переводящих ее из одного состояния в другое. Для поддержания этой хронологической последовательности основных событий в модели используется время.

Литература:

1. Максимей И. В. Имитационное моделирование сложных систем. В 3 частях. Часть 1. Математические основы; БГУ - Москва, 2009. - 264 c.

2. Захарикова, Е.Б. Моделирование динамики систем и сетей массового обслуживания / Е.Б. Захарикова, П.П. Макарычев // В мире научных открытий. - Красноярск: Изд-во «Научно-инновационный центр», 2012, № 8(32) (Математика. Механика. Информатика) - с. 222-235.

3. Чикуров Н. Г. Моделирование систем и процессов; РИОР, Инфра-М - Москва, 2013. - 400 c.