Сулейменов З.И. к.ф.-н.,доцент,

Наукенова М.Д., Касымбекова М.Т.,- магистр

Казахский национальный технический университет им. К.И. Сатпаева

ФУНКЦИИ ГРИНА УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ ДЛЯ НЕКОТОРЫХ НЕСТАНДАРТНЫХ ОБЛАСТЕЙ

Аннотация

В работе получины явные выражения функции Грина уравнения тепло-проводностей для некоторых нестандарных областей.

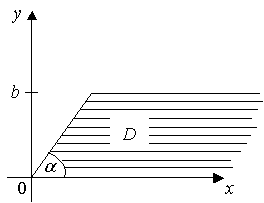
1.Пусть требуется найти функцию Грина следующей однородной краевой задачи в области , представленный на рис.1.

(1)

(2)

, (3)

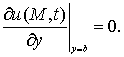(4)

Функцией Грина краевой задачи (1)-(4) называется решение следующей задачи [1]-[2]:

, (5)

, (6)

,, (7)

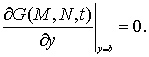(8)

Где ,произвольные точки области , функция Грина, оператор Лапласа , дельта – функция Дирака с особенностью в точке , постоянный коэфициент.

К уравнениям (5)-(8) по переменной применяем конечное синус преобразование Фурье по формуле

, (9)

где корни уравнения .

Задача (5)-(8) относительно перепишется в следующем виде:

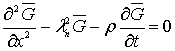(10)

, (11)

, (12)

К уравнениям (10)-(12) по переменной применяем преобразования Лапласа по формуле

(13)

Задача (10)-(12) относительно перепишется в следующем виде :

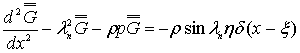(14)

(15)

Решение задачи (14)-(15) имеет вид[3]-[4]:

(16)

где .

От изображения (16) переходим к оригиналу по :

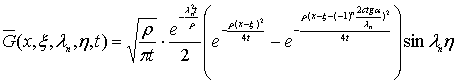(17)

Переходя из (17) к оригиналу по , получим решение задачи (5)-(8) в следующем виде:

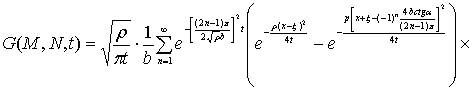
(18)

В частном случае, при, из (18) получаем функцию Грина для полуполосы:

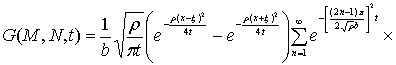
(19)

2. Функция Грина задачи Дирихле для данной области имеет вид:

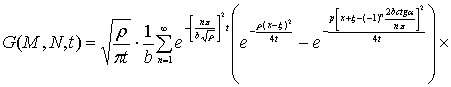
(20)

Функция Грина задачи Дирихле для полуполосы получаем в виде:

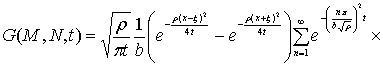
(21)

3. Аналогичным методом получаем Функцию Грина задачи (1),(2),(4) при условии на боковой границе

,

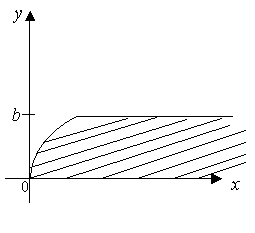
для области, представленной на рис. 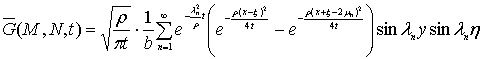2.

(22)

где .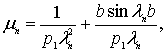

Функция Грина задачи Дирихле для области, представленной на рис.2 получаем в виде:

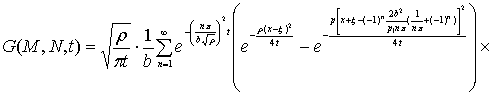
(23)

Cуммы в формулах (18)-(23) – быстросходящие и легко вычисляются при решении практических задач.Кроме того, названные формулы могут быть использованы при теоретическом исследовании краевых задач уравнений математической физики.

Цитированная литература

1.Кошляков Н.С.,Глинер Э.Б.,Смирнов М.М. Основные дифференциальные уравнения математической физики. М.,1962.

2.Арсенин В.Я.Методы математической физики и специальные функции. “Наука”, М.,1974

3.Сулейменов З.И.,Вестник Евразийского Национального Университета, Серия технических наук, 2006, № 4,с.23-29.

4.Сулейменов З.И. Математический журнал. 2007, том 7, №1(23), с. 81-85.