Долгарев И.А. и Долгарев А.И.

МНОГОМЕРНЫЕ ГАЛИЛЕЕВЫ ПОВЕРХНОСТИ I.

ГИПЕРПОВЕРХНОСТИ, ЦИЛИНДРИЧЕСКИЕ ПОВЕРХНОСТИ

АННОТАЦИЯ. Поверхности 3-мерного пространства-времени Галилея являются исключительным случаем в теории поверхностей галилеевых пространств. Евклидова составляющая галилеевой поверхности размерности больше 3 есть евклидова поверхность размерности больше 2. Имеется серия статей, в которых свойства евклидовых поверхностей изучаются на основе свойств цилиндрических поверхностей. Цилиндрические поверхности используются ниже и в галилеевой геометрии.

КЛЮЧЕВЫЕ СЛОВА: пространство-время Галилея, его евклидова составляющая; гиперповерхности и цилиндрические поверхности пространства Галилея; евклидова составляющая галилеевой поверхности; метрическая форма и форма кривизны галилеевой поверхности, заданной одной функцией; выражение коэффициентов формы кривизны  через коэффициенты метрической формы; определяемость поверхности.

            Галилеево скалярное произведение векторов превращает линейное пространство в галилеево векторное пространство и аффинное пространство в пространство-время Галилея. Коммутативное и линейное 3-мерное пространство Галилея изучается в [1], в этой же работе рассматривается некоммутативная галилеева геометрия подобий (геометрия пространства с растраном) и некоммутативная геометрия галилеевых движений плоскости (геометрия пространства с сибсоном). Растран и сибсон обобщают линейное пространство. Ниже начато изучение поверхностей многомерного коммутативного пространства-времени Галилея на основе цилиндрических поверхностей, как в серии работ по евклидовым многомерным поверхностям, см. [2]. Такой подход вносит некоторую специфику в теорию. Рассмотрены поверхности заданные одной скалярной функцией. В этом случае коэффициенты формы кривизны поверхности выражаются через коэффициенты метрической формы и поверхность определяется с точностью до положения в пространстве.

1.      Пространство-время Галилея

В действительном линейном пространстве  аффинного пространства  вводится галилеево скалярное произведение векторов. В результате линейное пространство становится галилеевым векторным пространством , аффинное пространство превращается в пространство-время Галилея .

Объекты аффинной геометрии, в частности прямые и плоскости аффинного пространства являются объектами, в том числе соответственно прямыми и плоскостями пространства Галилея  . Удобство этого факта состоит и в том, что свойства взаимного расположения прямых и плоскостей не изменяются с введением метрических понятий.

Рассматривается пространство-время Галилея  размерности .

Пусть  векторы из  , и , , тоже векторы из . Галилеевым скалярным произведением векторов   и  называется

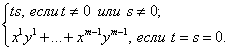 =                                           (1)

Далее: галилеевой нормой вектора  называется = и

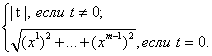 =                                            (2)

В  неравенство треугольника не выполняется. Векторы , , называются  галилеевыми, или временными векторы  называются  евклидовыми. Определение (1) в компонентах кортежей из  выделяет первую компоненту и в дальнейших рассуждениях за первой компонентой сохраняется специальный статус. Галилеево векторное пространство  рассматривается как прямая сумма , подпространства , согласно определению (1), являются евклидовыми, нижний индекс говорит об их принадлежности галилееву пространству,  .

Векторы из  и точки пространства  называются еще  событиями. Компоненты  являются временными, имеют смысл времени; компоненты  являются пространственными. Подчеркнем, что пространство-время Галилея обладает 1-мерным временем. Это означает, что все галилеевы векторы , , лежат в одном и том же временном подмножестве, хотя подпространства не составляют. Пространство-время Галилея  содержит евклидову составляющую , состоящую из событий вида , и представляющую собой  мерное евклидово пространство, оно является евклидовым подпространством наибольшей размерности пространства-времени Галилея .

  Расстоянием    между событиями   и  называется:

 =

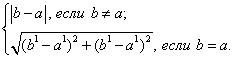
Репер  = пространства  считается ортонормированным. Формулы замены реперов считаем дифференцируемыми, поэтому можно проводить все рассмотрения в выбранном репере.

 Координатные плоскости <O, ,>,   являются плоскостями Галилея – это 2-мерные галилеевы пространства, гиперплоскость    является евклидовой. Через всякую точку  галилеева пространства  проходит единственная гиперплоскость Евклида,  ее уравнение ; таким образом, имеет место

1.      ЛЕММА. В каждый момент времени в пространстве-времени Галилея сущест-

вует единственная гиперплоскость Евклида.

Остальные гиперплоскости пространства Галилея, содержащие событие  А, есть гиперплоскости Галилея. В пространстве  временная составляющая 1-мерна. Поэтому все галилеевы векторы пространства, временная компонента которых имеет один и тот же знак, задают одно и то же временное направление в . Временное направление в  в точке  задается открытым полупространством, границей которого является евклидова гиперплоскость пространства , проходящая через точку .

2.      ЛЕММА. Всякий  галилеев вектор перпендикулярен всякому евклидову вектору.

# Проверяется по определению (1) галилеева скалярного произведения векторов. #

Дифференцируются галилеевы функции покомпонентно (обоснование в [1]).

2.      Поверхности многомерного пространства-времени Галилея

Пусть ,  временной интервал. Погружение  мерного многообразия  в мерное пространство-время Галилея , ,  называется поверхностью пространства-времени Галилея и обозначается , здесь  число параметров поверхности. Описывается поверхность  галилеевой векторной функцией

, , .                (1)

Поверхность является регулярной; ввиду регулярности поверхности, от параметризации (1) всегда можно перейти к параметризации

, ,                           (2)

, , . Поверхность  задана  явными функциями  , . Сначала рассматриваются галилеевы поверхности , заданные одной явной функцией

:  =,                             (3)

Параметры  от параметров  не зависят. Функцию  представляем в виде . Составляющая  является временной, составляющая

, ,                 (4)

является пространственной, т.е. евклидовой.

3.      Гиперповерхность, заданная одной явной функцией

Пусть . Имеем гиперповерхность

:  =.                                          (5)

Существуют векторы касательных к линии: ; к линиям . Их координаты:

, .

они независимы. Евклидовы векторы  порождают мерное евклидово подпространство  в . Имеется  независимых касательных векторов поверхности , вместе с обыкновенной точкой  поверхности они определяют касательную плоскость размерности :

 = ;

Таким образом, поверхность  является мерной (т.е. гиперповерхностью). В каждой точке она обладает единственной нормалью.

            Обобщением поверхности (5) пространства Галилея  служит поверхность

,                                         (6)

здесь , это параметрическая поверхность ; компоненты , от параметров  не зависят. Поверхность  является цилиндрической, она содержит прямые , где  точка поверхности. Обоснование того, что поверхность цилиндрическая, содержится в [2]. (Функция , определяющая поверхность, зависит от     параметров.) Касательными векторами поверхности  являются

 ;  где  ,

и ее касательная плоскость:

 = ;

т.к. касательная плоскость мерна, то размерность цилиндрической поверхности  равна  , в каждой точке поверхности существует единственная нормаль.

                        Цилиндрическая поверхность тоже относится к гиперповерхностям пространства , но будем выделять цилиндрические поверхностях размерности .

Евклидова составляющая поверхности (6) имеет вид (4), обладает свойствами, полученными в [2]. Приведем выдержки из [2], затем адаптируем их к евклидовой составляющей галилеевой цилиндрической поверхности. В [2] рассматриваются евклидовы поверхности , , компоненты , от параметров  не зависят. Установлено, [2, лемма 2], что поверхность ,, пространства  является цилиндрической, содержащей плоскость , размерность этой плоскости равна . По [2, лемма 5], нормальная плоскость  поверхности , обозначаемой , во всякой ее обыкновенной точке является 1-мерной. Вектор нормали поверхности  равен , последние  компонент которого равны 0 , его скалярный квадрат равен . и равен ,  модуль есть . Точнее, имеется поливектор . По [2, свойство 11], вектор  является ортогональным к векторам касательных  линий поверхности и векторам  прямых , лежащих на поверхности . Вектор  является единичным вектором нормали поверхности  в точке . По [2, теорема 12], вектор  =  пространства  евклидова пространства  ортогонален касательной плоскости  только если он коллинеарен вектору .

Поверхность (6) обладает евклидовой составляющей , , см. (4). На основании [2, лемма 2], для поверхности  (6) из  выполняется

3. ЛЕММА. Евклидова составляющая  поверхности   (6), , под-

пространства   пространства  является цилиндрической, содержащей плоскость , размерность этой плоскости равна . Галилеева поверхность  тоже является цилиндрической, она содержит галилееву плоскость  размерности .

4. ЛЕММА. Нормаль евклидовой составляющей  поверхности    во всякой ее обыкновенной точке является 1-мерной, лежит в евклидовой гиперплоскости с векторным пространством , и является нормалью галилеевой поверхности.

            # Утверждение соответствует лемме 5 из [2]. Вектор нормали  поверхности , являясь евклидовым, перпендикулярен галилееву вектору , см. лемму 2.#

Нормаль  поверхности  определяется вектором

,                                                       (7)

первая и последние  компонент которого равны 0 , его скалярный квадрат равен , т.к.  евклидов вектор; модуль его: .

5. СВОЙСТВО. Вектор (7) является ортогональным к векторам касательных  линии и линий поверхности и векторам  прямых , лежащих на поверхности . Вектор

                                                   (8)

является единичным вектором нормали поверхности  в точке .

            #  Действительно, ,   и . #

По аналогии с доказательством теоремы 12 в [2], устанавливается

6. ТЕОРЕМА. Вектор  =  пространства  ортогонален касательной плоскости  только если он коллинеарен вектору (7).

4.  Фундаментальные формы поверхности

            Рассматриваем  поверхности  (6) пространства , , . В координатах  на поверхности  имеем кривую в естественной параметризации, естест- венным параметром является время :

.                         (9)

Выписана галилеева линия, ее вектор касательной галилеев,

=.

Модуль галилеева вектора (9), согласно определению (2), равен 1:

.                                                                 (10)

Через всякую точку пространства  проходит евклидова гиперплоскость , лемма 1, в ее пересечении с поверхностью  лежит евклидова линия

, ,

вектор ее касательной евклидов

=, 

скалярный квадрат дифференциала евклидова вектора  равен

=.                                                         (11)

В соответствии с (2) на основании (10) и (11) метрическая форма  галилеевой поверхности  такова:

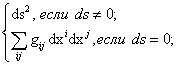
 =    .                                (12)

Коэффициенты метрической формы : галилеев  и евклидовы , равны:

;  и  .                          (13)

Имеется необходимость рассматривать евклидову составляющую метрической формы поверхности  , т.е. вторую строку определения (12):

.                                                  (14)

Мы рассматриваем поверхности пространства Галилея, размерность которого превосходит 3. Исключительный случай   рассмотрен ранее, в том числе в [1]. Имеется расхождение с общим случаем, рассматриваемом ниже. Дело в том, евклидова составляющая галилеевой поверхности пространства  есть плоская область, а для поверхности пространства , , есть поверхность евклидова пространства .

            Нормальной кривизной линий  на поверхности  относительно нормали  (8) является

.

Согласно (6), =+,  нормальная кривизна линий на поверхности равна

.                                                    (15)

Также определена нормальная кривизна линий на евклидовой поверхности, [2]. Получаем:

=. Обозначим

.                                                               (16)

Теперь кривизна линий на поверхности  относительно нормали  (8) такова

.                                                   (17)

Формой кривизны поверхности   относительно нормали  называется

,                                                    (18)

ее коэффициенты есть (16).  Формула (17), с учетом (15) и евклидовой части метрической формы (14), принимает вид

,

нормальная кривизна линий на поверхности равна отношению формы кривизны к евклидовой части  метрической формы  поверхности. Можно говорить о нормальной кривизне линий на поверхности , а не о кривизне линий на поверхности относительно нормали , так как нормаль поверхности единственна, [2, свойство 5, теорема 12].

            Евклидова составляющая метрической формы и форма кривизны галилеевой поверхности совпадают соответственно с формами метрической и кривизны евклидовой поверхности. Поэтому для метрической формы и формы кривизны галилеевой поверхности  выполняются свойства евклидовой поверхности, заданной одной явной функцией и полученные в [2]. Сформулируем эти свойства.

5. Выражение коэффициентов формы кривизны поверхности

через коэффициенты метрической формы

            7. ТЕОРЕМА [2, теорема 13]. Коэффициенты формы кривизны  поверхности  выражаются через коэффициенты евклидовой составляющей  метрической формы  поверхности и их производные первого порядка. Формулы зависимости таковы:

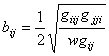,  ,  .                       (19)

            # По второй из формул в (13), . Производные величин  равны

.                                                    (20)

По (20) при , , это первая формула в (19). По (20) находим

, .

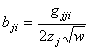Т.к. , то, с использованием третьей формулы в (13), находим

,

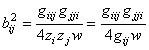откуда получается вторая формула в (19). #

            8. ЛЕММА [2, лемма 14]. Выполняется соотношение 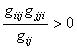 . Выражения  и  имеют один и тот же знак.

6. Определяемость поверхности мерного пространства

            Установлено, см. [3, теоремы 9.1, 9.6, 9.7, 9.10], что поверхность  евклидова пространства , , определяется однозначно, с точностью до положения в пространстве , своими формами: метрической и кривизны, при выполнении вполне определенных условий на коэффициенты указанных квадратичных форм в виде формул Гаусса – Петерсона – Кодацци. Это содержание основной теоремы теории евклидовых поверхностей. Она справедлива для евклидовой составляющей галилеевой поверхности, следовательно, и для галилеевой поверхности. Получив евклидову составляющую галилеевой поверхности по евклидовой составляющей метрической формы галилеевой поверхности, и добавив временную составляющую, имеем галилееву поверхность. На основании доказанной выше теоремы 7, основная теорема теории поверхностей, заданных одной явной скалярной функцией в многомерном пространстве, принимает такой вид.

            9. ТЕОРЕМА. (основная теорема теории поверхностей) Поверхность   пространства-времени Галилея , , однозначно, с точностью до положения в пространстве, определяется своей метрической формой.

Литература

1.      Долгарев  А. И. Классические методы в дифференциальной геометрии одулярных пространств. Монография. – Пенза: ИИЦ ПГУ, 2005.- 306с.

2.      Долгарев А.И. Многомерные поверхности I. Выражение коэффициентов второй квадратичной формы евклидовой поверхности через коэффициенты первой квадратичной формы.// Materialy X Miedzynarodowej naukowi-praktycznej konferencji “Moderni vymozenosti vedy – 2014”, Dil 34. Matematyka. Fizyka. Praha. Publiching House “Educa      tion and Skience”. s.r.o. – 2014. С. 30 – 40.

3.       I. Ivanova-Karatopraklieva, P.E. Markov, I. Kh. Sabitov. Bending of surfaces. III. Fundamentalnaya i prikladnaya matematika, vol 12. (2006), № 1,  pp. 3 – 56.