К.т.н. Тарадай Д. В., Тимин А. В., Шуранова Ю. А.

ОАО «ВТИ», Россия

Оценка остаточного ресурса с расчетом напряжений в сечениях роторов турбоагрегатов при нестационарных воздействиях

Большая часть паровых турбин находится в условиях старения и имеет время наработки близкое к ресурсу. Важнейшей составляющей турбоустановки является система роторов, собранных в валопровод. При эксплуатации на валопровод действуют сложные системы статических и динамических нагрузок, зависящих от веса роторов, эксплуатационных расцентровок, центробежных сил, динамических характеристик опор, и др. В рабочих лопатках, дисках и валах от совокупных нагрузок возникает сложное напряженное состояние. Кроме того, при пуско-остановочных режимах из-за неравномерных температурных полей в металле деталей валопровода возникают сложные термоциклические напряжения. Накопление повреждаемости в валопроводе исчерпывает и снижает ресурс турбоустановки, который рассчитывается по нормативной методике с учетом накопления деформации пластичности и ползучести высокотемпературных роторов, преимущественно РВД и РСД. Однако опыт эксплуатации показывает, что в роторах может накапливаться дополнительная повреждаемость, связанная с повышенными уровнями вибрации, чрезмерными эксплуатационными расцентровками, жесткими синхронизациями.

В связи с тем, что отказы оборудования случаются внезапно и их диагностика измерительными методами не всегда возможна и показательна, то возникает необходимость иметь методики для уточненного расчета оценок остаточного ресурса оборудования.

Для определения допускаемых напряжений в [1] приводится диаграмма целостности разрушения (рис. 1), отображающая вероятность разрушения материала. На диаграмме представлены допускаемые напряжения при переменном нагружении. Циклическое напряжение в некоторой точке детали состоит из постоянной составляющей и переменной составляющей . На рисунке также обозначено: - предел текучести материала, - предел усталости. В случае если значение напряжения находится внутри треугольника, образованного и деталь не разрушится.

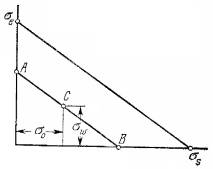
Рис. 1

У А. Г. Костюка [2] характеристика усталости при стационарном циклическом нагружении изображается кривой усталости для симметричного цикла (рис. 2), имеющей два участка. На первом участке зависимость предела усталости от числа циклов до разрушения аппроксимирована формулой =K, где l и K – постоянные материала, зависящие от температуры. В двойных логарифмических координатах зависимость изображается прямой линией.

На втором участке - постоянная величина, равная истинному пределу усталости при симметричном цикле , т.е. такому напряжению, ниже которого материал может выдержать без разрушения циклические напряжения неограниченно долго время.

Точка перелома зависимости от N обычно наблюдается при = 10⁷-10⁸ циклов.

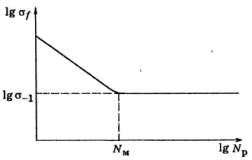
Рис. 2

Проведем оценку ресурса отдельно для крутильных колебаний валопровода. Расчетная оценка циклической прочности и ресурса валопровода базируется на линейной теории суммирования повреждаемостей, согласно гипотезе Пальмгрена-Майнера. В соответствии с этой гипотезой, выраженной формулой (1) разрушение материала вала с образованием усталостной трещины может произойти, если накопленная суммарная повреждаемость достигнет единицы. Здесь под однократной повреждаемостью при одном режиме нагружения понимается величина отношения числа циклов на этом режиме с известным напряжением к предельно допустимому числу циклов до разрушения материала, которое определяется по кривой сопротивления усталости.

(1)

где:

- число циклов нагружения с амплитудой напряжения кручения ;

- число циклов до разрушения при циклическом нагружении с амплитудой ;

s - количество режимов (уровней) нагружения.

Если времени эксплуатации валопровода поставить в соответствие заданный техническими условиями на турбину (либо назначенный) ресурс Т, то повреждаемости можно использовать для определения выработанной доли ресурса, именуемой как эквивалентное время наработки [4]:

(2)

Поэтому для приближенной оценки числа циклов до разрушения при циклическом кручении используются кривые усталости роторных сталей при симметричном растяжении-сжатии.

Для роторной стали Р2МА обобщенная кривая сопротивления усталости представлена на рис. 3, а необходимая для расчета циклической прочности аппроксимирующая ее функция имеет вид [5]:

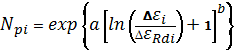, (3)

где:

– число циклов полных деформаций до разрушения;

– полная деформация i-го режима нагружения;

– полная деформация разрушения стали в i-ом режиме нагружения;

; N₀=1,710⁷; ;

K_T, K_R и K_d – коэффициенты, соответственно учитывающие влияние температуры, среднего напряжения цикла и масштабного фактора.

; ;;

;

;.

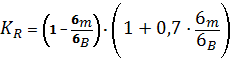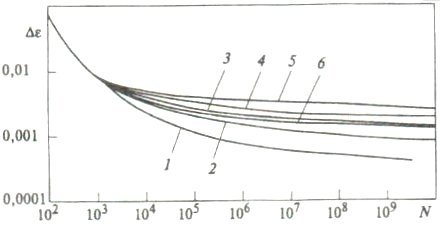
Рис. 3. Сопротивление усталости стали Р2МА в широком диапазоне изменения параметров нагружения

1 – 0,2; 2 – 0,4; 3 – 0,6; 4 – 0,8; 5 – 1,0; 6 – кривая малоцикловой усталости.

При известной амплитуде циклических напряжений кручения, расчетная оценка эквивалентного времени наработки (выработки ресурса) может быть выполнена по формулам (2), (3). Для измеренных крутильных колебаний, возникающие касательные напряжения в любом сечении валопровода определяются:

(4)

где:

прогнозируемое (искомое) значение параметра крутильных колебаний с частотой f в i-ом сечении валопровода;

расчетное значение параметра крутильных колебаний с частотой f в i-ом сечении валопровода;

– измеренное значение амплитуды составляющей крутильных колебаний с частотой f в k-ом сечении измерений;

расчетное значение амплитуды крутильных колебаний с частотой f в k-ом сечении измерений.

В процессе эксплуатации турбоагрегатов валопровод испытывает воздействие различных видов циклического и статического нагружения. Наиболее опасными являются термические напряжения, возникающие в высокотемпературных роторах высокого и среднего давления при пусках, остановах, изменениях активной нагрузки и пр. Именно по этим напряжениям в критических сечениях по длине РВД и РСД рассчитывается остаточный ресурс и оценивается эквивалентное время наработки. Уточнение этих расчетов, несомненно, связано с дополнительным учетом всех видов возникающих напряжений, в частности напряжений от веса роторов, расцентровок, прогиба роторов, поперечных колебаний валов и напряжений от крутильных колебаний.

Если обозначить накопленную повреждаемость от j-го вида нагружения в k-ом критическом сечении валопровода , k=1, 2, … , К, где K – число учитываемых видов нагружения:

, (5)

то эквивалентное время наработки будет определяться как максимальное из всех вычисленных значений:

(6)

здесь j = 1, 2, … , J, где J – число видов нагружения;

k = 1, 2, … , K, где К – число учитываемых критических сечений.

Обратимся к кривой сопротивления усталости для стали Р2МА, представленной на рис. 3. Выполним анализ этой кривой с учетом масштабного фактора () [6], температурного фактора (), фактора асимметрии цикла нагружения () и фактора, учитывающего вид нагружения (). Примем во внимание, что число циклов нагружения при частоте циклических напряжений 50 Гц составляет 2·10¹⁰. Как следует из кривой (рис. 3) при данном числе циклов и принятых значениях коэффициентов усталостных повреждений валопровода не произойдет, если амплитуда циклических напряжений кручения не будет превышать 80 МПа. Однако помимо переменной составляющей напряжений присутствует еще и постоянная (статическая закрутка). Это способствует достижению таких значений напряжений как 150 МПа и более, которые являются опасными для валопровода и могут привести к его разрушению.

Задача вычисления выработки ресурса с учетом всех влияющих видов нагружения по формуле (6) представляет собой весьма трудоемкую задачу, которая требует выявления всех реальных нагрузок в процессе эксплуатации. Отсюда следует, что необходима схематизация нагружения, причем оценивать ресурс ротора необходимо с учетом фактора, максимально влияющего на повреждаемость валопровода (погибы ротора, вибрация, крутильные колебания). Для оценки повреждаемости ротора от воздействия крутильных колебаний следует сделать расчет на повреждаемость от крутильных колебаний, а затем на совокупную повреждаемость от всех остальных критериев и за отчетный период времени сравнить по какому из них повреждаемость окажется больше.

Работа выполняется при поддержке Гранта Президента Российской Федерации МК-6431.2013.8.

Выводы:

1. Предложено оценивать ресурс турбоустановки по уточненной методике с учетом различных факторов, влияющих на повреждаемость роторов.

2. Задача вычисления выработки уточненного ресурса требует выявления всех реальных нагрузок в процессе эксплуатации.

3. При оценке повреждаемости роторов от крутильных колебаний необходимо учитывать статическую закрутку валопровода.

Литература

1. Прочность и колебания элементов конструкций / Тимошенко С. П. Гл. редакция физико-матем. лит-ры изд-ва Наука, 1975, стр. 639-641.

2. Костюк А. Г. Динамика и прочность турбомашин: учебник для вузов / 3-е издание, перераб. и доп. – М.: Изд. Дом МЭИ, 2007, стр. 61-62.

3. Радин Б.А., Конторович Т.С. Использование принципа эквивалентной наработки для оценки надёжности оборудования ПГУ // Электрические станции, № 1, 2012. – c.16-18.

4. Трухний А.Д., Корж Д.Д., Лебедева А.И. Обобщённые характеристики усталости роторной стали Р2МА для использования в системах технической диагностики выработки ресурса. // Теплоэнергетика. 2003. № 6. С. 16-21.

5. Бовсуновский А.П. и др. Усталостное повреждение и разрушение роторов паровых турбин в результате крутильных колебаний. – Проблемы прочности, 2010, №1, с. 44-51.