Технические науки/Энергетика

УДК 621.31

К.т.н. В.А. Шабанов, магистрант Н.А. Чернышов

Уфимский государственный нефтяной технический университет, Россия

АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ИЗНОСА ИЗОЛЯЦИИ ОБМОТКИ СТАТОРА ЭЛЕКТРОДВИГАТЕЛЕЙ ПРИ ПУСКЕ

 

Основными методами регулирования производительности магистральных нефтепроводов в настоящее время являются изменение числа насосов и метод циклической перекачки, при котором циклически изменяется количество включенных магистральных насосов [1, 2]. Частые пуски электродвига­телей при подборе числа насосов и в режимах циклической перекачки приводят к ускоренному износу изоляции вследствие нагрева обмотки пусковыми токами. Поэтому оценка величины износа изоляции электродвигателей при пуске является актуальной задачей. В статье рассматриваются аналитические выражения для оценки износа изоляции обмотки статора при пуске электродвигателей.

Интегральное выражение для износа изоляции при пуске ЭД. Износ изоляции обмоток электродвигателей за время t измеряют в единицах времени и представляют в виде интеграла от экспоненциальной функции [3, 4 ]:

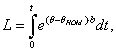                                                                                                         (1)

где θ – температура изоляции, °С;; θн –  номинальная температура изоляции;

.                                                                                                                  (2)

где Δθ – температурный коэффициент, зависящий от типа изоляции.

Для оценки износа изоляции необходимо знать тем­пературу обмотки θ и ее изменение во времени. При строгом анали­зе процессов нагревания обмотки электродвигатель должен рассматриваться как сложное тело, так как тепловые параметры металла обмотки, изоляции и стали магнитопровода неодинако­вы. Нагрев обмотки статора происходит не только за счет потерь мощности в самой обмотке, но и за счет потерь в стали статора и в обмотке ротора. Кроме того на нагрев влияют условия охлаждения электродвигателя. При учете всех факто­ров, влияющих на температуру обмотки, анализ значительно усложняется. На практике приме­няют упрощенные уравнения нагрева, полученные для однородного тела за счет выделяю­щихся в нем потерь мощности и энергии. При этом принимают, что потери энергии в теле и коэффициент его теплоотдачи не зависят от его темпера­туры, которая принимается одинаковой дли всего тела. При таких допущениях нагрев тела происходит по экспоненциальному закону. Примем аналогичные допущения для обмотки статора при пуске, а именно: коэффициент теплоотдачи обмотки не зависят от ее темпера­туры; изменение температуры обмотки во время пуска происходит только под действием потерь в обмотке статора от пускового тока и не зависит от потерь в стали и в обмотке ротора [5]. При этом изменение температуры обмотки статора во время пуска будет происходить по экспоненциальному закону:

                                                                  (3)

где θнач – начальная температура обмотки, θп.уст – установившаяся температура обмотки, которая имела бы место при длительном нагреве пусковым током, без учета нагрева от потерь в стали и в обмотке ротора; τ – постоян­ная времени нагрева обмотки.

Изменение температуры обмотки при пуске показано на рисунке 1 (кривая 1).

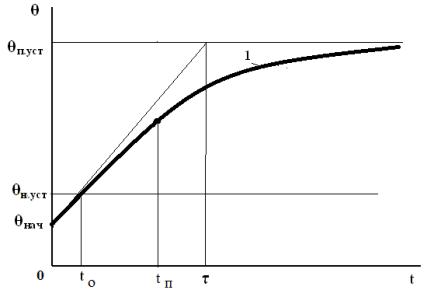
Рисунок 1 – Нагрев обмотки статора при пуске

 

Если принять, что переходный процесс нагрева обмотки заканчивается через три постоянных времени, то для установившейся температуры обмотки при нагреве ее пусковым током можно записать:

                                                                                 (4)

где ∆Рп – потери мощности в обмотке статора при пусковом токе; с - удельная теплоемкость обмотки; G - масса обмотки.

Аналогично для установившейся температуры обмотки при нагреве ее номинальным током:

                                                                              (5)

где θн.уст –установившаяся температура обмотки, при нагреве номинальным током без учета нагрева от потерь в стали и обмотке ротора; ∆Рном – потери мощности в обмотке статора при номинальном токе.

Потери мощности в обмотке пропорциональны произведению квадрата тока на активное сопротивление обмотки: . При этом из (4) и (5) находим:

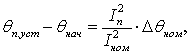
                                                                   (6)

где Iп – пусковой ток; Iном – номинальный ток; δθном – номинальное превышение температуры:

                                                                                            (7)

После подстановки (6) в (3) уравнение нагрева обмотки статора принимает вид:

                                                                          (8)

где kп =Iп /Iном  - кратность пускового тока, равная отношению тока в обмотке статора при пуске Iп к номинальному току Iном.

Подставляя (8) в (1), получаем для износа изоляции при пуске электродвигателя следующее уравнение:

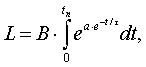                                                                                             (9)                       где

                                                                                                                                (10)

                                                                                                                               (11)

Интеграл (9) не имеет точного решения. Приближенно его решение можно найти либо через определение интегральной суммы; либо методом подстановки с последующим использованием разложения в ряд Тейлора (Маклорена); либо непосредственно разложением в ряд подынтегральной функции; либо применяя линеаризацию экспоненциальной функции.

Определение интегральной суммы.  Если построить график функции:

                                                                                                                                    

то износ изоляции за время пуска tп по (9) будет равен площади под кривой F=f(t). Разобьем время пуска на ряд одинаковых отрезков Δt и для каждого интервала Δt найдем значение Fср для середины интервала Δt.  Тогда износ изоляции определяется по выражению:

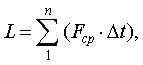                                                                                              (12)    

Сумму (12) называют интегральной. Чем меньше интервал Δt, тем ближе интегральная сумма (12) к интегралу (9).

Интегрирование методом подстановки.

Применим подстановку:    

                                                                                                              (13)

При этом 

                                                                        

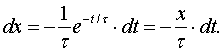
Откуда

                                                                                                      

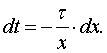
Пределы интегрирования в (9) после подстановки будут х=1 и          

При этом подстановкой (13) интеграл (9) сводится к виду:

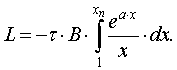                                                                                      (14)                 Интеграл (14) является табличным, но решение его представляется в виде бесконечного степенного ряда [6]. Если ограничится первыми четырьмя членами ряда, то решение интеграла (14) имеет вид:

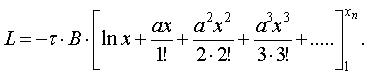                                    (15)        

После подстановки пределов интегрирования, получаем выражение для износа изоляции в функции параметра «х»:

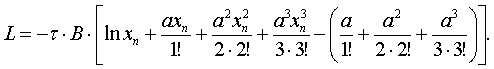
Для перехода к функции времени подставим из (13) значение хп при t = tп, получим:

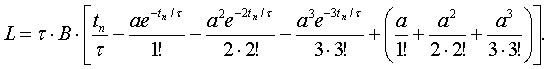     (16)

Интегрирование путем разложения в ряд экспоненциальной функции. Показательная функция раскладывается в степенной ряд Маклорена [7]:

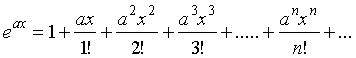                                        (17)    

Подставим в (17) вместо х его значение из (13). Тогда для показательной функции   под знаком интеграла (9) получим следующий ряд:

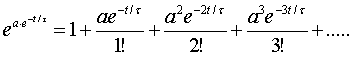   .                                     (18)    

Подставляя (18) в (9), получаем для износа изоляции следующий интеграл: 

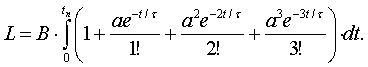                                      Выполняя интегрирование и подставляя пределы, находим:

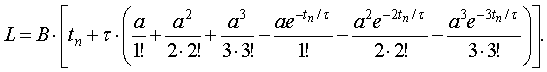      (19)

Выражение (19) совпадает с выражением (16), полученным с использованием табличного интеграла. Но разложение в ряд непосредственно подынтегральной функции позволяет быстрее получить функцию износа изоляции в функции времени.  Кроме того, разложение в ряд позволяет оценить погрешность от отбрасывания части членов ряда.

Заключение.

В статье рассмотрены аналитические выражения для износа изоляции обмотки статора при пуске, основанные на решении интегральной функции износа изоляции от температуры. Такой интеграл не имеет точного решения. Показано, что приближенно его решение можно найти либо через определение интегральной суммы; либо методом подстановки с последующим использованием разложения в ряд Тейлора; либо непосредственно разложением в ряд подынтегральной функции.

 

Литература:

1 Коршак А.А., Нечваль А.М. Трубопроводный транспорт нефти, нефтепродуктов и газа: Учеб. для вузов – Уфа: ООО «ДизайнПолиграфСервис», 2001. – 571 с.

2 Шабанов В.А., Павлова З.Х., Калимгулов А.Р. О влиянии частотно-регулируемого электропривода магистральных насосов на цикличность нагружения трубопровода // Электронный научный журнал "Нефтегазовое дело", 2012. - №5. - С. 23-30. URL: http://www.ogbus.ru/authors/Shabanov/Shabanov_14.pdf

3 Хвостов В.С. Электрические машины: Машины постоянного тока.
Учебное пособие. -  М.: Высшая школа, 1988. - 336 с.

4 Кузнецов Н.А. Надежность электрических машин. М.; Издательский дом МЭИ, 2006. – 432 с.

5 Сыромятников И. А. Режимы работы асинхронных и синхронных электродвигателей. - М.: Госэнергоиздат, 1963. - 532 с.

6. Двайт Г.Б. Таблицы интегралов и другие математические формулы. –Санкт Петербург: Издательство АО ВНИИГ, 1995. - 196 с.

7. Бермант А.Ф. Краткий курс математического анализа. – М.: Наука, 1965. – 663 с.