д.т.н., профессор. Пиль Э.А., Санкт-Петербургский государственный морской технический университет,

Россия.

ТРЕХМЕРНЫЕ областИ существования

экономической оболочки

Двухмерные графики, к сожалению, не всегда позволяют анализировать расчитываемые величины, в особенности, когда эти величины зависят от нескольких параметров. В данной статье представлены 3D зависимости построенной области DVeluc существования экономической оболочки, которая рассчитывается как разница между Velc и Velc, т.е. DVeluc = Veuс - Velc. Здесь Veuc - максимальный объем экономической оболочки, ед.³ и Velc - минимальный объем экономической оболочки, ед.³.

Так на рис. 1 показана 3D зависимость при Х1е = 10, Х2е = Х3е = 1…0,1. Как видно этот рисунок значительно показателен, чем аналогичная 2D зависимость, представленная на рис. 2. На рис. 3 также показана 3D зависимость при Х1е = 10, Х2е = Х3е = 1…0,1, но только с другими параметрами.

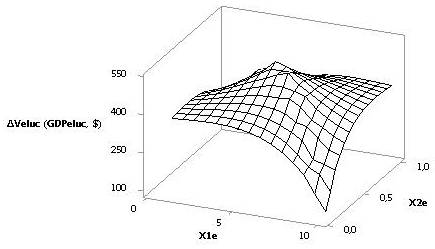
Рис. 1. 3D зависимость DVeluc при Х1е = 10, Х2е = Х3е = 1…0,1

На следующем рис. 4 показана также 3D зависимость, но при Х1е = Х3е = 1…0,1 и Х2е = 10. Здесь DVeluc зависимость имеет более простую форму с увеличением значений в конце.

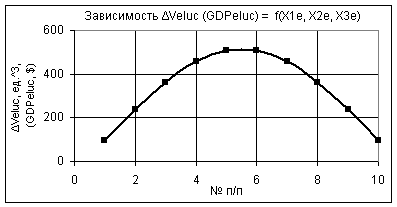
Рис. 2. 2D зависимость при Х1е = 10, Х2е = Х3е = 1…0,1

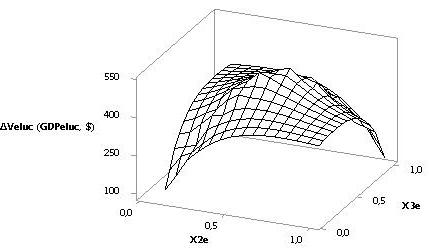
Рис. 3. 3D зависимость DVeluc при Х1е = 10, Х2е = Х3е = 1…0,1

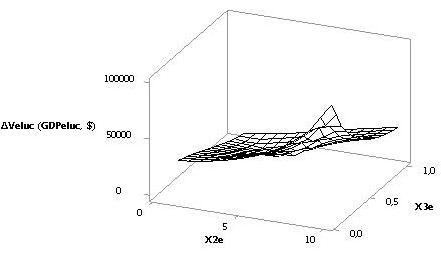
Рис. 4. 3D зависимость DVeluc при Х1е = 10, Х2е = Х3е = 1…0,1

Рис. 5 дает нам наглядное представление, как изменяются значения DVeluc, когда параметры будут следующие: Х1е = Х2е = 1…0,1, Х3е = 10. Здесь видно, что значения DVeluc практически представляют из себя большую часть плоскость.

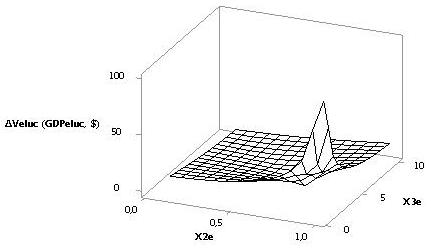
Рис. 5. 3D зависимость DVeluc при Х1е = Х2е = 1…0,1, Х3е = 10

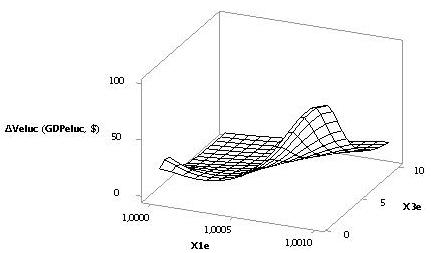
Рис. 6. 3D зависимость DVeluc при Х1е = 1, Х2е = 1…0,1, Х3е = 10

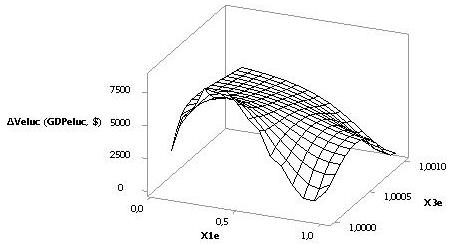
Рис. 7. 3D зависимость DVeluc при Х1е = 1…0,1, Х2е = 10, Х3е = 1

На последних двух рисунках 6 и 7 также показаны зависимости DVeluc при Х1е = 1, Х2е = 1…0,1, Х3е = 10 и Х1е = 1…0,1, Х2е = 10, Х3е = 1 соответственно, которые имеют достаточно сложный вид.