Рукин М.Д., Волков Ю.В., Черняев А.Ф.

 

МОДЕЛИ ПРОЦЕССОВ В ЗЕМНЫХ И СОЛНЕЧНЫХ ОБОЛОЧКАХ.

(статья 1)

 

Введение.

В этой работе мы рассмотрим ряд простых моделей кооперативных явлений и процессов в земных и солнечных оболочках. Как известно (1,2), для открытых систем, далеких от состояния термодинамического равновесия, ха­рактерны синергетические явления. Понятие "синергетика" введено физиком Г. Хакеном, ко­торый предложил объединить все методы описа­ния кооперативных явлений самоорганизации в различных областях наук именовать единым термином.

Геология, геофизика, климатология и физика солнечных проявлений активности с ее полицикличностью, несомненно, имеют дело с открытыми непрерывными системами. Эта об­ласть современной науки активно развивается и далека от завершения. Поэтому наше изложение будет скорее собранием примеров, моделей, идей, чем строгим систематическим изложением новой научной дисциплины.

Струйные течения в земной атмосфере и океанах (3), дифференциальное вращение сол­нечной атмосферы (4, 5, 6) находят естественное описание как процессы, в которых на фоне энергонасыщенной турбулентности и конвекции происходят явления отрицательной вязкости (2), понятие которой с физических позиций мы пояс­ним ниже. В то же время конкретные механизмы и модели этих процессов изучены еще недостаточно (6).

В связи с этим мы хотим обратиться к про­стейшим статистическим моделям кооператив­ных явлений, таких как броуновское движение частиц (7) и рассмотреть эффекты его обратимо­сти во времени (8, 9). Изучая броуновское дви­жение с помощью уравнения Фоккера-Планка- Колмогорова и Монте-Карловского моделиро­вания, мы имеем в виду аналогию движений вих­рей турбулентности и хаотически движущихся частиц.

Теоретическая возможность обращения времени в феномене броуновского движения, на наш взгляд, позволяет подойти к пониманию физической сущности явления отрицательной вязкости, а это последнее составляет основу кооперативных синергетических процессов в природе, в том числе и в ряде геологических явлений. В заключении этой работы мы приведем некото­рые конкретные примеры синергетических про­цессов, в том числе и из области геосистем, к ко­торым, как нам представляется, можно прило­жить описанные теоретические и статистические модели.

Теория.

Пусть Р = Р (x,t) - вероятность нахождения броуновской частицы в интервале (-х, х) в мо­мент времени (t ). Взаимодействие частицы со средой выразим с помощью функции j (у), которая обладает следующими свойствами: j (у) = j (-у);  - имеет редкий максимум вблизи точки взаимодействия. Пусть далее (t, -t) - некоторый достаточно малый временной интервал.
Составим уравнение баланса броуновских частиц, имея в виду теорему об умножении вероятностей.

  (1)

 Ввиду малости t и согласно теореме Тейлора:

         (2)

Здесь члены порядка t2, t3, и т. д. опущены как малые. Функцию Р (х + у, t) в правой сторо­не (1) также можно разложить по теореме Тей­лора и, учитывая независимость величин (х) и (у) и вводя сокращенное обозначение Р для величин Р (х, t), напишем (1) в виде уравнения:

 

  (3)

 

Ввиду того, что функция  (у) - четная, что выражается равенством  (-у) =  (у), второй, четвертый и т.д. члены в (3) обратятся в нуль, а из оставшихся членов каждый последующий будет мал по сравнению с предыдущим. Принимая это во внимание, а также, что , найдем частную производную из выражения (4):

 

      (4)

Вводя обозначение , запишем (4) в виде уравнения (5):

              (5)

 

Это уравнение отличается от известного уравнения диффузии лишь двойным знаком при D. Положительный знак не содержит ничего но­вого, а отрицательный соответствует тому, что можно назвать "отрицательной диффузией" или же, как это легко показать (7), однозначно с ней связанной "отрицательной вязкостью" (2). Урав­нение (5) - простейшее из уравнений, в котором эти эффекты отражены непосредственно.

Обратим внимание, что уравнению (5) можно удовлетворить, подставляя в него функ­цию вида:

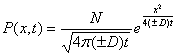         (6)

 

Однако здесь обнаруживается, что решение (6) с отрицательным D не обладает физическим смыслом вероятности, т.к. величина Р в этом случае - мнимая. Выходом из такого затруднения может явиться замечательное свойство диффузионного процесса броуновских частиц (8,9) - его обратимость. Введем величину t = -t (обращенное время). Тогда решение уравнения (5) запишется в виде уравнения (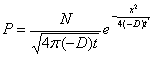7):

      (7)

 

В этом выражении (Р) уже является действительной положительной величиной ≤ 1, как и следует по смыслу вероятности.

С помощью (6) и (7) найдем среднее квадратичное величины смещения N броуновских частиц из начала координат.

    (8)

Здесь

Итак, из теории следует, что величина

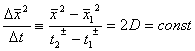    (9)

Проверим это соотношение, обратившись к статистическому моделированию на компьютере.

 

МОНТЕ-КАРЛО (МК) МОДЕЛИРОВАНИЕ.

 

Процесс броуновского движения частиц может быть смоделирован статистически на компьютере (10-12). Как и выше, рассмотрим здесь лишь простейший одномерный случай. Алгоритм моделирования включает: 1. Задание начальных значений координат всех N частиц. 2. Задание величины шага (Н) по времени. 3. Организацию циклов выдачи результатов моделирования на дисплей. 4. Установку начального значения суммы средних квадратов смещений. 5. Организацию цикла промежуточных вычислений без выдачи результатов (примерно около 10 итераций). 6. Организацию цикла по всем N частицам для главной процедуры случайных смещений координат. Случайное число из датчика РАН интервала (0, 1) преобразовывалось к интервалу (-Н/2, +Н/2 ) по формуле DR = Н* (RAN#-.5) и прибавлялось к координате (х), текущей i - й частицы и т.д. После десяти шагов по времени вычислялась величина и ее разность с предыдущей Di. Обращенный во времени процесс моделировался в соответствии с теоремой об обратимости (8, 9) ша­гами по координате t'. Некоторые результаты МК моделирования приведены в таблицах 1- 4.

Обсудим их на примере табл.1. Таблица представляет величины: номер (десятикратного) шага (n), величину D (разность ). Указаны: число частиц N и величина шага N. Левая колонка, помеченная знаком (-), дает процесс диффузии N броуновских частиц в обращенном времени t ', а провал (+) – в прямом времени (t). Моменту t = 0 соответствует флуктуация: .

         Закону Эйнштейна (7) уравнения (8), (9) соответствует равномерное расширение квадра­та размеров "облака" броуновских частиц и, как это видно из табл. 1, вблизи t = 0 это имеет место.

Однако, чем шире расплывается облако бро­уновских частиц, тем вероятнее в игру вступают флуктуации: около 80 и 90-го шагов "облако" вместо расширения начинает временно сужаться. Отметим, что эти пульсации никак не связаны с волновыми свойствами микрочастиц, т.к. в усло­виях модели не закладывались квантовые волно­вые свойства.

При обращенном времени (t’ ) процесс идет таким образом, что облако частиц "сжимается" и создает флуктуацию в начале координат х, t, а дальнейший ход процесса ведет уже к диффузии облака. При N = 25 с увеличением шага от 0.05 до 0.5 минимум на 80-90 - м шаге оставался не­изменным. Однако при N = 50 и 80 этого не бы­ло. В табл.4 приведены результаты аналогично­го процесса для ветви t' с использованием датчи­ка псевдослучайных чисел, описанного в работе (10), достоинством которого является то, что все расчеты можно воспроизвести заново (при необ­ходимости), но как видно, минимума на 80-90 - м шаге уже нет.

Процесс броуновского движения частиц в средах надо рассматривать как отвечающий уравнению диффузии с чередующимися знаками у Д. Если бы движение отвечало одному знаку (+),то энергия должна была бы рассеиваться, а движение прекратилось бы. Напротив, при знаке (-) происходило бы неограниченное ускорение частиц. Только чередование знаков отвечает ра­венству ускорений и замедлений в незатухающем движении малых частичек. МК моделирование показало, что теоретическая модель справедлива при возрастающих N, при малых N необходимо принимать во внимание флуктуации.

 

ПРИМЕРЫ ГЕОСИНЕРГЕТИЧЕСКИХ ПРОЦЕССОВ.

 

Описав кооперированные синергетические процессы на простейших модельных и теоретических образцах броуновского движения, не­сколько проясняющих их сущность, мы обратим­ся к природным явлениям, которые либо уже оп­ределенно имеют указанные свойства, либо до сих пор изучены слабо и вызывают трудности в интерпретации.

Как это указано в (2), в физике есть ряд явлений, где проявляется свойство отрицатель­ной вязкости среды, если последняя имеет доста­точно высокую энергонасыщенность. Приводи­мый там пример - процессы в лазерах: фотонный луч, проходя через среду, набирает энергию и отдает ее в другом месте, перейдя в иные усло­вия. Другое замечательное явление - сверхпрово­димость. На наш взгляд, уравнения со знакоче­редующейся вязкостью, пожалуй, лучше подхо­дят для описания этого удивительного явления.

Обратимся к разделам, которые гораздо ближе нам - к геологии, геофизике, климатоло­гии, самоорганизующимся системам во Вселен­ной. Многие примеры, конечно, уже описаны в (2, 3, 4, 13). Отмечается, что струйные течения в атмосфере со скоростью порядка 400 км/час имеют столь узкую локализацию, что было бы невозможно при наличии обычных диссипативных процессов. Океанские течения, как Гольфст­рим, Куросио, обладают таким же свойством. Плохо объясняются и океанские противотечения - во всех модельных расчетах с нормальной вяз­костью они получаются широкими и размыты­ми.

В работе (11, 13) дана классификация океан­ских течений по струйному типу: ПТ - пассатное течение, ПП - пассатное противотечение, ЭТ - экваториальное течение, ЗВ - течение "западных ветров". Применение формулы (6) для описания отдельного струйного течения (при этом величи­на Р уже означает скорость или импульс струй­ного потока) позволило нам решать уравнение гидродинамики методом Ритца. Однако сами уравнения гидродинамики не модифицировались включением членов с отрицательной вязкостью. Такой выбор пробной функции для решения уравнений отчасти исправляет недостатки самих уравнений, приближая решение к тому, что на­блюдается в результате эксперимента. Такой ме­тод носит лишь приближенный временный ха­рактер. Он должен  быть исправлен в будущем включением свойств знакочередующихся  коэффициентов вязкости и турбулентной диффузии.

В работе (14) подробно рассмотрены астросинергетические динамические системы, в том числе кольца планет, циклы солнечной активно­сти, некоторые галактические и метагалактические структуры, феномен самоорганизации пер­воначально бесструктурной материи, так называемого космического хаоса, в последовательность упорядоченных во времени и пространстве событий.

Можно еще привести примеры полос в атмосфере Юпитера и Сатурна, связанными со струйными «Геострофическими» течениями, и что еще более важно с точки зрения геоклиматологических приложений - то же свойство обна­руживается в атмосфере Солнца (5, 6). Из-за не­достаточной статистики солнечных пятен суще­ствование бароклинных волн в атмосфере Солн­ца пока остается теоретическим предположени­ем, но трудности с объяснением полициклично­сти пятен и дифференциального вращения, по видимому, можно преодолеть, только вводя в учет синергетические явления, в частности, явле­ния отрицательной вязкости.

Мы хотели бы особо отметить здесь, что уравнение Т. Дж. Каулинга (5, с.440)

        (10)

которое имеет вид уравнения диффузии для маг­нитного поля Н с коэффициентом диффузии магнитного поля Дн = 1/4ps также, по видимому, надо обобщить на знакопеременное с ± Д .

Генерация поля Н в этом случае пойдет также, как генерируются флуктуации в начале координат в случае уравнения (5) или МК-моделях.

Нам кажется, в пользу такого предполо­жения говорит как характер генерации (или ис­чезновений) поля в пятнах (в зависимости от преобладания "+" или ), но и таким же путем можно объяснить выбросы узких протуберанцев (типа струй, см. (5, с.326-327). Протуберанец 12 июня 1946 года). Объяснить формирование та­ких выбросов в среде с положительными коэф­фициентами диффузии и вязкости нелегко.

"Опускаясь" ближе к Земле, отметим, что узкоструйность и расслоенность характерна не только для атмосферы и гидросферы Земли, но и литосфера, и мантия согласно исследованиям по­следних лет, также обладают этим характерным качеством.

Опубликовано немалое количество работ, посвященных циклам неорганических систем, для этого достаточно просмотреть 2-х томный 1-й - 4-й выпуски материалов третьей международной конференции "Циклы природы и общества" (14). В этих материалах мы находим немало работ, посвященных цикличности в геологических сис­темах. Это работы, в которых рассмотрены во­просы теории спиральной циркуляции мантии, это работы о межполюсных дрейфах блоков ли­тосферы; это вопросы седиментационной цик­личности и связанной с ними проблемы прогноза нефтегазоносности, подробно рассмотренные во многих фундаментальных трудах отечественных и зарубежных специалистов; это цикличность в развитии экзогенных геологических процессов, это цикличность формирования коллекторов и залежей углеводородов в зависимости от термо­динамических условий, это цикличность осадконакопления в современных морских бассейнах и многое, многое другое. И если нам удастся свя­зать проблемы цикличности в природных систе­мах с понятием «синергетика», то тогда список примеров может быть значительно пополнен, но это уже требует написания новой работы о при­кладном использовании приведенных в этой за­метке идей и математического аппарата.

Как и в других циклах природных систем, в основе геологической цикличности должны быть некоторые общие принципы циклических процессов в системах вообще. Земля, как любая открытая система, переходит из какого-то на­чального хаотического состояния в какое-то ко­нечное состояние. И здесь возможны два вариан­та: конечное состояние совпадет с начальным, хаотическим, т.е. все вернется "на круги своя", или же система в результате самоорганизации придет в упорядоченное состояние.

Наиболее вероятным для планеты Земля нам представляется первый вариант развития системы, так как ход развития системы в данном случае определяется как внутренними, так и внешними причинами. А внешние причины, наименее изученные, представляются наиболее значимыми и непредсказуемыми по своей сути. Отсюда приходим к тому, что для Земли харак­терен вынужденный (открытый) цикл, обладаю­щий пространственно-временной периодично­стью и иерархической структурой. И поэтому дла изучения происходящих в ней процессов не­обходимо использовать математический аппарат неравновесной термодинамики. Что мы и сдела­ли в этой дискуссионной работе.

ЛИТЕРАТУРА

1.    Пригожин И. Неравновесная статисти­ческая механика. М., Мир, 1964, с.314.

2.    Старр В. П. Физика явлений с отрица­тельной вязкостью. М., Мир, 1971, с. 260.

3.    Монин А.С. Введение в теорию климата. Л., 1982.

4.                        Монин А.С. Солнечный цикл. Л., 1980. с.68.

5.                        Солнце. Ред. Дж. Койнер, М., ИЛ, 1957, с.609.

6.    Вандакуров  Ю.В. Конвекция на Солнце и 11-летний цикл. Л., 1976, с. 156.

7.    Броуновское движение. Сб. ст., М.-Л., 1936. с. 607.

8.    Яглом А.М. О статистической обрати­мости броуновского движения. "Математический сборник", 1949, т. 24, вып. 3, с.456-492.

9.    Kolmogoroff A. Zur Umrthrbarkeit der statistisclien Naturgesetze. Math. Ann., 113, 766-772 (1937).

10. Волков Ю.В. Исследования статистиче­ских свойств временного ряда сильных землетря­сений. Изв. АН, Физика Земли, 1991, л. 3.

11. Волков Ю.В., Ясаманов Н.А. Вариации климатических зон и поверхностные океанические течения в юрском периоде. Вестн. МГУ, сер. геол. М.,1997.

12.                Методы Монте-Карло в статистиче­ской физике. М., Мир, 1982, с.400.

13.                Ю.В.Волков, М.Д.Рукин, А.Ф.Черняев. Некоторые математические модели палеоклиматологии. //Акад. Тринитаризма, М., Эл.№77-6567, публ. 20707, 06.06.2015, с.357.

14.                Розгачева И.К. Самоорганизующиеся системы  во Вселенной. подписн. серия «Космонавтика, астрономия», Изд-во «Знание», М., 1989, №11, с.62.

15.                Циклы природы и общества. Выпуск 1-4. Ставрополь, 1995. Материалы третьей международной конференции.

 

ТАБЛИЦЫ – ПРИЛОЖЕНИЯ

 

N=25             H=0.05                                                   Таблица 1.1

 

-

+

n

D

D

1

2

3

4

5

6

7

8

9

10

0.001957

.003629

.005849

.006861

.007017

.008414

.010000

.009946

.008675

.011018

0.001957

.001672

.002220

.001012

.000156

.001357

.001590

-.000590

-.001271

.001509

0.001604

.005358

.008408

.013510

.015580

.017560

.018090

.015370

.015060

.014220

0.001604

.003754

.003049

.005107

.002070

.001976

.000532

-.002719

-.000318

-.000837

 

N=25             H=0.1                                                   Таблица 1.2

 

-

+

n

D

D

1

2

3

4

5

6

7

8

9

10

0.008145

.014380

.017550

.018280

.020730

.034350

.030500

.048410

.048170

.041070

0.008146

.006239

.003169

.007256

.002453

.013620

.002143

.011920

-.002450

-.007097

0.006951

.015220

.027870

.033530

.034250

.041400

.047910

.062850

.061040

.076540

0.006951

.008272

.012640

.005665

.000712

.007157

.006511

.014940

-.001205

.014890

 

 

 

 

N=25             H=0.5                                                   Таблица 2.1

-

+

N

D

D

1

2

3

4

5

6

7

8

9

10

0.118000

.381400

.593800

.844500

.089500

1.179000

1.843000

1.659000

1.580000

1.855000

0.118000

.263400

.212400

.250600

.050560

.284300

.663300

-.183300

-.079460

.275100

0.276500

.360600

.544900

.802300

.950000

1.035000

1.207000

1.475000

1.538000

2.020000

0.276500

.084120

.184300

.257400

.147700

.084650

.172200

.268400

.062300

.482200

 

N=50             H=0.05                                                   Таблица 2.2

 

-

+

n

D

D

1

0.002100

0.002100

0.002000

0.002000

2

.004600

.002500

.003400

.001400

3

.006800

.002200

.004900

.001600

4

.007200

.000400

.006500

.001600

5

.009900

.002700

.008000

.001500

6

.010700

.000800

.010200

.002200

7

.012800

.002100

.012000

.001800

8

.018200

.005400

.015200

.003200

9

.021300

.003100

.017200

.002000

10

.024400

.003200

.019500

.002300

 

N=50             H=0.1                                                   Таблица 3.1

 

-

+

n

D

D

1

0.011800

0.011800

0.011200

0.011200

2

.019200

.007400

.020300

.009100

3

.030300

.011100

.029500

.009200

4

.032000

.001700

.041600

.012100

5

.036700

.004700

.051300

.009700

6

.043300

.006600

.050500

-.000800

7

.051600

.008300

.056500

.005900

8

.068500

.016900

.080200

.023700

9

.084600

.016100

.093400

.013200

10

.091400

.006700

.100200

.006900

 

 

 

 

 

N=50             H=0.5                                                   Таблица 3.2

-

+

n

D

D

1

0.300900

0.300900

0.205500

0.205500

2

.691300

.390400

.317100

.111600

3

.923400

.232000

.478400

.161300

4

.916600

-.006800

.627000

.148500

5

1.133000

.216400

.823600

.196600

6

1.322000

.189300

.930600

.107000

7

1.660000

.337600

1.076000

.145400

8

1864000

.203800

1272000

.196300

9

2228000

.364500

1.397000

.124600

10

2.394000

.165700

1.529000

.132000

 

N=80             H=0.05                                                   Таблица 4.1

                                                           -

+

n

D

D

1

0.002100

0.002100

0.002300

0.002300

2

.003700

.001600

.004100

.001800

3

.006500

.002800

.005900

.001800

4

.008600

.002100

.007300

.001400

5

.010800

.002200

.008500

.001200

6

.013900

.003100

.010700

.002200

7

.016800

.002900

.011900

.001200

8

.019300

.002500

.015700

.003700

9

.020600

.001300

.019400

.003700

10

.021800

.001200

.023600

.004200

 

N=25             H=0.05                 Таблица 4.2

-

n

D

1

0.003243

0.003243

2

.004974

.001731

3

.008659

.003685

4

.010430

.001788

5

.014670

.004243

6

.017250

.002577

7

.016000

-.001248

8

.020510

.004509

9

.020980

.000472

10

.018670

-.002313