Рукин М.Д., Волков Ю.В., Черняев А.Ф.

 

МОДЕЛИ ПРОЦЕССОВ В ЗЕМНЫХ И СОЛНЕЧНЫХ ОБОЛОЧКАХ

(статья 3)

 

Методы математического моделирования строения и свойств минералов приобретают все большее развитие в науках о Земле, в частности, в геологии [1, 2].  Ниже рассматриваются некоторые аспекты статистического и динамического методов моделирования с целью их применения к исследованию физических свойств минералов, характерных для различных геосфер. Следуя за работой [3, c.348], мы выделяем: 1) центральное ядро; 2) промежуточную оболочку; 3) эклогитовую оболочку; 4) базальтовую оболочку; 5) гранитную оболочку и 6) атмосферу. На рис.1 приводится схема распространения главных элементов по выделенным оболочкам.

 

 

 

 

 

 

Рис.1. Схема распространения главнейших химических  элементов в отдельных зонах Земли (по А.Е.Ферсману, с нашими добавлениями).

 

Как видно из схемы, шестнадцать выделенных химических элементов распределяются достаточно неравномерно по геосферам: ядро в основном состоит из железа и никеля; промежуточная оболочка – из серы, кислорода, железа, марганца и магния; эклогитовая и базальтовая оболочки – из кислорода, кремния, алюминия, кальция, магния, титана, хрома и марганца; гранитная оболочка имеет наиболее разнообразный состав, но кислород, кремний, алюминий, кальций, натрий, калий и фосфор – доминируют; в атмосферу из выделенных элементов вошли: кислород, водород и углерод. Современные геохимические данные практически не изме5нили существенно данную схему  [4] и в моделировании свойств минералов вполне возможно на нее ориентироваться. В таблице 1, содержащей информацию об электронной конфигурации атомов 50 важнейших химических элементов [5], расположенных по порядку возрастания атомных номеров, названные выше 16 элементов выделены соответствующими цветами по их принадлежности к оболочкам геосфер.

 

Электронная конфигурация атомов элементов.

Таблица 1.

Элемент

Атомное число, Z

Число и распределение электронов по оболочкам

 

 

1 s

2s

2p

3s

Зр

3d

4s

4р

4d

4f

5s

5p

5d

5f

6s

6p

6d

6f

7 s

Н

1

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Не

2

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Li

3

2

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Be

4

2

2

 

'

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

В

5

2

2

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

С

6

2

2

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

N

7

2

2

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

О

8

2

2

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

F

9

2

2

5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ne

10

2

2

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Na

11

2

2

6

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Mg

12

2

2

6

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

А1

13

2

2

6

2

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Si

14

2

2

6

2

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Р

15

2

2

6

2

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

S

16

2

2

6

2

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Cl

17

2

2

6

2

5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Аг

18

2

2

6

2

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

К

19

2

2

6

2

6

 

1

 

 

 

 

 

 

 

 

 

 

 

 

Ca

20

2

2

6

2

6

 

2

 

 

 

 

 

 

 

 

 

 

 

 

Sc

21

2

2

6

2

6

1

2

 

 

 

 

 

 

 

 

 

 

 

 

Ti

22

2

2

6

2

6

2

2

 

 

 

 

 

 

 

 

 

 

 

 

V

23

2

2

6

2

6

3

2

 

 

 

 

 

 

 

 

 

 

 

 

Cr

24

2

2

6

2

6

5

1

 

 

 

 

 

 

 

 

 

 

 

 

Mn

25

2

2

6

2

6

5

2

 

 

 

 

 

 

 

 

 

 

 

 

Fe

26

2

2

6

2

6

6

2

 

 

 

 

 

 

 

 

 

 

 

 

Co

27

2

2

6

2

6

7

2

 

 

 

 

 

 

 

 

 

 

 

 

Ni

28

2

2

6

2

6

8

2

 

 

 

 

 

 

 

 

 

 

 

 

Cu

29

2

2

6

2

6

10

1

 

 

 

 

 

 

 

 

 

 

 

 

Zn

30

2

2

6

2

6

10

2

 

 

 

 

 

 

 

 

 

 

 

 

Ga

31

2

2

6

2

6

10

2

1

 

 

 

 

 

 

 

 

 

 

 

Ge

32

2

2

6

2

6

10

2

2

 

 

 

 

 

 

 

 

 

 

 

As

33

2

2

6

2

6

10

2

3

 

 

 

 

 

 

 

 

 

 

 

Se

34

2

2

6

2

6

10

2

4

 

 

 

 

 

 

 

 

 

 

 

Br

35

2

2

6

2

6

10

2

5

 

 

 

 

 

 

 

 

 

 

 

Kr

36

2

2

6

2

6

10

2

6

 

 

 

 

 

 

 

 

 

 

 

Rb

37

2

2

6

2

6

10

2

6

1

 

 

 

 

 

 

 

 

 

 

Sr

38

2

2

6

2

6

10

2

6

2

 

 

 

 

 

 

 

 

 

 

Y

39

2

2

6

2

6

10

2

6

1

2

 

 

 

 

 

 

 

 

 

Zr

40

2

2

6

2

6

10

2

6

2

2

 

 

 

 

 

 

 

 

 

Nb

41

2

2

6

2

6

10

2

6

4

1

 

 

 

 

 

 

 

 

 

Mo

42

2

2

6

2

6

10

2

6

5

1

 

 

 

 

 

 

 

 

 

Tc

43

2

2

6

2

6

10

2

6

6

1

 

 

 

 

 

 

 

 

 

Ru

44

2

2

6

2

6

10

2

6

7

1

 

 

 

 

 

 

 

 

 

Rh

45

2

2

6

2

6

10

2

6

8

1

 

 

 

 

 

 

 

 

 

Pd

46

2

2

6

2

6

10

2

6

10

 

 

 

 

 

 

 

 

 

 

Ag

47

2

2

6

2

6

10

2

6

10

1

 

 

 

 

 

 

 

 

 

Cd

48

2

2

6

2

6

10

2

6

10

2

 

 

 

 

 

 

 

 

 

In

49

2

2

6

2

6

10

2

6

10

2

1

 

 

 

 

 

 

 

 

Sn

50

2

2

6

2

6

10

2

6

10

2

2

 

 

 

 

 

 

 

 

 

         Вопрос о распределении температуры в недрах Земли все еще не решен, более определенными являются данные о плотности, давлении и модуле всестороннего сжатия [6]. Внутреннее (твердое) ядро занимает промежуток 5121- 6371 км глубины. Ему соответствуют следующие значения параметров: плотность – 12,197 - 12, 46г/см3, давление – 3, 275- 3, 608 х 1022 дин/см2 и модуль сжатия равен 10, 842-14,244 х 1012 дин/см2. Внешнее ядро занимает интервал: 2878 - 4982 км глубины. Значения параметров следующие: плотность – 9, 927 – 12, 121 г/см3, давление – 1, 347 - 3, 198 х 1012 дин/см2 и модуль сжатия равен 6, 522 -13,282 х 1012 дин/см2. Нижняя мантия: 984 - 2800 км глубины. Ему соответствуют следующие значения параметров: плотность – 4,529 - 5, 487 г/см3, давление – 0, 38 - 1, 301 х 1012 дин/см2 и модуль сжатия равен 3, 471 - 6,294 х 1012 дин/см2. Верхняя мантия: 15 – 400 км глубины. Параметры: давление – 0,004 – 0, 135 х1012 дин/см2, плотность – 3, 313 – 3, 775 г/см3, модуль сжатия – 1, 017 – 1, 886 х 1012 дин/см2.. Таковы некоторые характеристики физических условий, полученных по данным сейсмологии. Совершенно очевидно, что при изучении процессов минерагении важно учитывать свойства минералов, какими они обладают внутри соответствующих оболочек, а не на поверхности Земли и при обыкновенных лабораторных экспериментах.

         Методы математического моделирования физических свойств минералов при высоких давлениях можно разделить на две группы:1) статистические и 2) динамические. Рассмотрим их по порядку. В основе статистических методов лежат кинетические уравнения и термодинамические законы [7,8], а также метод численного статистического моделирования – метод Монте-Карло [9]. Последний может эффективно развиваться только при наличии современных компьютерных систем и обладает исключительными простотой и общностью: его можно применять как к кристаллическим, так и электронным подсистемам, а включение новых эффектов и явлений в рассмотрение не вызывает затруднений. Ограничения метода связаны лишь с недостаточными мощностями и оперативной памятью используемых компьютеров. А его недостаток – исключительно числовая (или графическая) форма представления результатов.

         В статистическом методе моделирования предполагается, что каждый сложный процесс может быть представлен суммой так называемых «элементарных» процессов. Постулируется, что рассматриваемый физический объект (атом, кристалл, минерал) имеет множество состояний и что элементарным процессом является такой переход между двумя состояниями, который по какой-либо причине нельзя разделить на две части. Эволюция системы во времени описывается основным кинетическим уравнением: (1):

 

         (1)

         Здесь - вероятность  того, что система находится в момент времени (t) в состоянии (n), а (m) – это состояние, в которое  система может перейти из состояния (n). Коэффициенты пропорциональности  называются вероятностью перехода (n) → (m) и представляют вероятность элементарного процесса, который должен быть рассчитан из квантовой механики [5] или определен другим способом (см. уравнение 2):

 

          (2)

         Здесь - постоянная Дирака, - матричный элемент перехода, t -  время, истекшее от начала  t = 0, d - функция, обеспечивающая выполнение закона сохранения энергии во время квантового перехода из состояния (n) в состояние (m),  энергии системы в состоянии( m) и (n). E – соответствует  энергии перехода (E =, если в переходе участвует фотон или фонон).

         Для вычисления матричного элемента необходимо знать волновые функции системы в состояниях m и n (функции и ). Последние находятся из решения уравнения Шредингера, например, в приближении самосогласованного поля [5]. Однако мы ниже покажем, как можно получить волновые функции любого атома на основании табл.1, а также и энергии состояний и эффективные радиусы «орбит». Уравнение (1) оказывается слишком сложным и требует упрощения. Пусть n имеет большое число значений с непрерывным или квазинепрерывным распределением по некоторому параметру S. Тогда систему можно описать функцией f (t,S), дающей вероятность того, что состояние с данным значением S занято в момент времени t. Пусть f (t,S) нормирована так, что интеграл , где N(t) – средняя концентрация частиц в пространстве S. Перепишем уравнение (1) для функции f в виде уравнения (3):

     (3)

         Здесь W(S, DS) – вероятность изменения параметра S в элементарном процессе на величину DS. Производную можно переписать в форме уравнения (4), т.е. в виде суммы частных производных:

 

        (4)

 

         Здесь - скорость дрейфа частиц по координате S. Для упрощения уравнения (3) разделим совокупность DS на две части. В первую включим лишь малые значения DS, которые много меньше всего диапазона изменения  S (DS << S). Усредненное по таким процессам время назовем временем релаксации (t) с нижним индексом r, значение которого вычисляется из выражения, приведенного ниже:

 

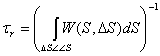.     (5)

 

         В другой части остаются большие значения DS (DS приближенно равно S). Соответствующие переходы можно рассматривать как акты создания и стока частиц с координатой S. Усредненное по этим процессам время  назовем временем жизни частиц:

 

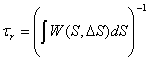.     (6)

 

         Определим мощности создания (источников) и стоков частиц:

 

        (7)

и

 

     (8)

 

         С учетом  DS   <<  S первое слагаемое в (3) можно разложить в ряд Тейлора:

 

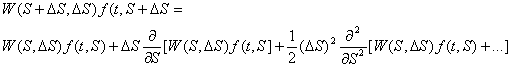(9)

 

         Тогда

 

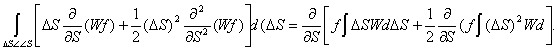 (10)

 

         Здесь W º W(S, DS) и f º f(t,S).

 

С учетом (7,8,10) можно переписать уравнение  (3) в виде:

 

          (11)

 

Здесь:

 

А =   B =    IS =

 

Уравнение (11) называется уравнением Фоккера-Планка. Если же А и В не зависят от S или, если использовать усредненные по S значения А=,   , то из (11) и (4) найдем:

 

 

                    (12)

 

Здесь DS – это коэффициент диффузии частиц по координате S. В  случае постоянного числа частиц (G=T=0) из уравнений (3) и (4) получается:

 

  (13)

 

   (14)

 

Здесь  - вероятность элементарного процесса соударения частицы, имеющей координату и скорость с переходом этих величин в и  - сила, действующая на частицу с массой (m) со стороны внешнего поля. Уравнения (13) и (14) называются уравнением Больцмана. Оно применяется для рассмотрения поведения зонных электронов и дырок в кристаллах, а также электронов и ионов в плазме. Оно более информативно, чем уравнение Фоккера-Планка, но сложности при его решении часто служат препятствием для практических применений. Это уравнение позволяет описывать поведение систем, далеких от состояния термодинамического равновесия и может применяться для описания фото-стимулированного и электро-стимулированного минералогенезиса. Приближение, в котором принимается значение St = - (f – f0) / tn, где f0 – функция распределения состояния равновесия, называется приближением времени релаксации. Если в St провести разложение f по малым изменениям величины и , то снова получится диффузионное уравнение (12).

Применение метода Монте-Карло к моделированию основного уравнения (1) состоит в следующем [10, c.39]. При таком подходе эволюция системы рассматривается как марковский процесс. Основное уравнение является балансовым уравнением. Изменение состояния системы связывается с процессами двух видов. Первая сумма справа описывает все процессы, которые пополняют рассматриваемое состояние, а вторая – процессы, которые опустошают его. При термодинамическом равновесии должно выполняться условие детального равновесия, обеспечивающее равенство этих сумм по модулю. Текущее «время» t связывается со шкалой n последовательных конфигураций. Можно пронормировать  временную шкалу так, чтобы одночастичных переходов осуществлялось  за единицу времени. Тогда единица времени будет равна 1 МК-Ш/частица. Корреляции сильно влияют на точность расчетов по методу Монте-Карло при заданном заранее числе МК-шагов. Их можно исследовать с помощью динамической интерпретации МК-усреднения в терминах основного уравнения. Наряду с этим модель применима в самых различных областях, таких, как броуновское движение микромолекул кристаллического состояния минералов, релаксация в спиновых и квадрупольных системах, явления образования и роста зародышей, спинового разложения смесей, агрегация, ограниченная диффузией, явление связанного необратимого роста минерала, диффузия на поверхности и в слоях и ее влияние на физические свойства минерала [10, c.38].

Динамическое моделирование физических свойств кристаллов берет свое начало от работ [11, 12] по исследованию радиационных эффектов в кристаллах. Этот подход наиболее прост, но требует мощных компьютеров, если количество атомов в кристалле достаточно велико. Численно решаются классические уравнения движения атомов и ионов (см. уравнение 15):

 

      (15)

 

Здесь расстояние между двумя атомами i и j; a – константа экранирования. По Н.Бору  а » , где а0 – радиус первой боровской орбиты атома водорода.

На рис. 2. Показаны результаты такого динамического моделирования атомных движений в кристалле. На рисунке видны как колебательные движения отдельных атомов, так и цепочки фокусирующих соударений по отдельным направлениям. В данном кристалле такие столкновения происходят преимущественно в направлении (1,0,0) и (1,1,0). Фокусировка столкновений в плотно упакованных рядах атомов – это типично кристаллический эффект упорядочивания.

 

 

 

 

 

Рис.2. Траектория движения атомов после передачи атому кинетической энергии 40 эв в указанном стрелкой направлении (авторский рисунок).

 

Расчеты показали, что с ростом температуры эффекты фокусировок и капилирования уменьшаются. В процессах соударения атомов развиваются высокие давления и, вероятно, это оправдывает возможность применения динамического моделирования к изучению физических процессов в минералах при высоких давлениях, свойственных земным недрам. Слабым местом этой методики является выбор кулоновского потенциала, экранированного по Н.Бору. Видимо,  более приемлемыми и более строгими будут потенциалы с экранировкой по Хортри-Фоку [5]. Однако расчеты самосогласованного поля ведутся без учета внешних давлений и искажений волновых функций. Сложность расчетов при этом не будет оправдывать их точность. Отметим, что, если бы были известны волновые функции атомов, выделенных рис.1 и в табл.1, то проблема нахождения коэффициентов Wmn в уравнении (1) и проблема определения Vi,j для процедуры динамического моделирования очевидно решались бы. Мы предполагаем для их решения осуществить следующий подход.

Пусть атомные электроны описываются моделью электронных колец Н.Бора. Это соответствует выбору волновой функции в форме уравнения (16):

      (16)

 

Здесь d - функция Дирака. Такой выбор волновой функции позволяет эффективно выполнить все интегрирования при расчетах экранированного потенциала и найти коэффициенты экранирования для каждого из квантовых состояний табл.1. Легко показать, что вычисление  константы экранирования сводится при этом к следующей сумме правил: 1) Znl* =Z – число внутренних электронов) – ¼ Vnl , где Vnl – число электронов внутри данной «оболочки» с параметрами n, 1; 2) внешние электроны в учет не принимаются. Заслуживает пояснения множитель ¼. Если исходить из выражения (16) и не учитывать спиновых координат состояний, то это приводит к множителю ½ , но из этого числа электронов, т.е. которые имеют спины, антипараллельные рассматриваемому, не должны принимать участия в экранировке из-за эффектов квантовой статистики – это и ведет к множителю ¼. Полагая далее, что истинные волновые функции – водородоподобны, найдем из [5]:

 

   (17)

 

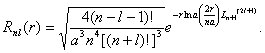     (18)

 

Здесь Ylm – шаровые функции; Lmn(2l+1) – полиномы Лагерра.

Расчеты, выполненные для атомов с этими волновыми функциями, показали хорошее приближение к полным энергиям атомов, а также к эффективным радиусам отдельных оболочек по всей периодической системе элементов. Однако описанный метод дает хорошее приближение лишь для свободных атомов, а не атомов под давлением в условиях земных оболочек.

Последняя задача решается с помощью следующего приема. Поскольку размер атома определяется его внешней оболочкой и электроны в ней  находятся в кулоновом поле атомного остатка, уравновешенного  отталкивающим эффектом за счет ортогонализации к волновым функциям внутренних электронов, то некоторое  произвольное увеличение заряда ядра на величинуDZ приведет к сжатию орбиты внешнего электрона и действию на последний дополнительной силы:

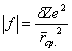      (19)

Здесь - среднее расстояние до ядра этой внешней оболочки, а площадь «поверхности» этой оболочки найдется геометрически:

         (20)

Отсюда легко найти  и избыточное  давление и изменения размеров атома, связанные с этим давлением.

Величина dZ дает необходимую поправку в Znl* для волновых функций и вероятностей элементарных процессов и парных потенциалов, а также результаты моделирований свойств кристаллических минералов для условий разных оболочек Земли.

 

ЛИТЕРАТУРА

1.    Урусов B.C., Дубровинский Л.С. ЭВМ - моделирование структуры и свойств минералов. М., Изд-во МГУ, 1989.

2.    Термодинамическое моделирование в гео­логии. М., Мир, 1992.

3.    Ферсман Ф.Е. Избранные труды, т. III, М., 1955.

4.                       Тейлор С.Р., Мак-Леннан С. М. Конти­нентальная кора, ее состав и эволюция. М., Мир, 1988.

5.    Ландау Л.Д., Лифшиц Б. М. Квантовая механика. М., Наука, 1974.

6.    Стейси Ф. Физика Земли. М., Мир, 1972.

7.                       Ландау Л.Д., Лифшиц Б. М. Статистиче­ская физика. М., Наука, 1964.

8.                       Трейвус Е.Б. Введение в термодинамику кристаллогенезиса. Л., 1990.

9.                       Методы Монте-Карло в статистиче­ской физике. М., Мир, 1982.

10.                        Биндер     К, Хеерман Д. Моделирование методом Монте-Карло в статистической физике. М., Наука, 1995.

11. Gibson J.B.,Goland A.N., Milgram V.,Vineyard G.N. Dynamics of radiation damage //Phys.Rev. 1960. V.120, №4. p/1229-1253.

12. Diens     G.J., Vineyard G.H. Radiation effects in solids. №4, 1957.