Karachun V.V.

National Technical University of Ukraine “KPI”

FOCUSING ENERGY OF AN ULTRASONIC BEAM IN GYRO

Focusing energy of an ultrasnic beam in gyro. We will show some original aspects of arising energy focusing of penetrating acoustic radiation. Let’s consider an average former (Fig. 1).

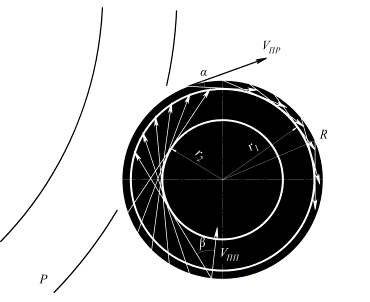
Fig. 1. Focusing energy of acoustic radiation

Suppose that the float is missing. A sound wave Р, which is falling from outside on the ARS body, generates in the material circular (along the former circle) oscillations , which extend in a parallel direction with velocity , i.e, along the lateral surface of the shell, and also bending (radial) oscillations in the plane of the former at velocity .

First of all, let us find out the mechanism of circular waves. Taking the lateral surface of the ARS body as a shell of a sufficiently large wave size, let’s consider any separate element of the inner surface of the former as a plate of zero curvature, where the velocity of longitudinal waves coincides with the circular velocity of the shell.

If the velocity of longitudinal waves is greater than the sound speed in liquid, ie,

,

Then the wave traveling along the parallel will radiare a sound wave in liquid, and the direction of its propagation together with the vector velocity will constitute theangle , which is calculated by the formula (Fig. 1):

.

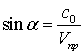As a result, much of the sound wave energy will be focused around a circle of radius (Fig. 1)

.

For example, if we take the radius of the inner cavity of the ARS body as , take aluminum alloy as material (, ), a liquid-and-static gimble - of glycerol (),and the frequency of the ultrasnic beam f=42 кГц, then the wave size will be 3,43.

It is not difficult to calculate the radius of the caustic surface (Fig. 1) –

.

It is clear that if , the angle and the wave travelling along the parallel will radiate a sound wave (that crosses the axis of the device here) in liquid. Thus, aberration will disappear and the caustic surface turned to the geometric locus of points of energy concentration that are located on the ARS axis. Similarly, if , then and the caustic surface is not formed by a bending wave. It is interesting to estimate the temperature impact on the degree of concentration of in a liquid-and-static part. The sound speed of in liquid at the temperature changes is calculated by the formula -

.

For glycerol . So when , the sound speed in liquid-and-static gimbal is reduced to 1851 . On the contrary at the same time at the sound speed is increasing to . The manufacturer warrants a continuous operation at within 7 minutes. That is the sound speed in liquid equals . It follows thence that stable temperature creates conditions for a process of "zone kaustikos" and thus influences the ARS error in flight.

For this reason, the transversal wave will result in energy concentration around the circular cylinder of radius:

.

Radius of the float equals , so it is obvious that the caustic surface of radius disappears and the radius surface – will be left.

Caustic surfaces of radius and clearly separate the areas of acoustic shadow in liquid.

Of course, when choosing a material for the body and liquid, we can affect the features of caustic areas to make them discrete-continuous.

If we use the beam acoustic methods, one can classify this phenomenon as a kind of aberration (from the Greek aberration - a deviation from the normal) sound waves. As we know, in aberration-free structures a caustic surface rotates around the axis, and therefore, in our example it will be located on the axis of the body.