Mel’nick V.N.

National Technical University of Ukraine “KPI”

APPROXIMEE DESIGN MODEL OF THE SHELL OF THE ДУСУ GYRODEVICE

We will analyze the impact of radial waves (in the former’s plate) of the shell of the body of the ДУСУ gyrodevice of angle rate and the extending (parallel or circular) springing waves, which appear at the impact of outer acoustic radiation of a supersonic flight. The radial wave, generated in the ДУСУ body and the wave, travelling along the parallel, will radiate sound waves in the liquid-and-stable part of the float gimbal. At the wave coincidence they will be the reason of formation of energy active zones (kausticos zones) in liquid.

We will build an approximee design model due to a large wave size , which simplifies the initial factors in the analytical structure of the phenomenon, replacing the shell by a discrete-continuous complex of thin plates of zero curvature, which radiate acoustic waves into liquid due to the bending motion and stringing oscillations along the parallel (Fig. 1). We begin with the study of the bending motion of the elementary (flat) section of the inner surface of the shell.

Radial (bending) oscillations of the body surface at the action of ultrasonic radiation

The resulting condition of significant wave size of the body, i.e. satisfaction of the ratio

, (1)

allows consider any separate element of the body surface as a thin, stringing, isotropic plate of a continuous length and thickness (Fig. 2).

We assume that a flat sound wave "1" with the angle falls on the plate. The axis Ox is parallel to the perturbation front. Let’s take pressure in the falling wave as

, (2)

where – a wave number of the air environment outside the body;  – pressure amplitude of the falling wave "1". If we take the wave numbers of the front and shadow sides as equal, then . If not, then you should use Snelius’s law:

.

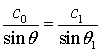In our case ; .

The pressure in the reflected "2" and passing "3" waves can be written as –

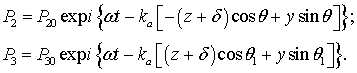(3)

Apparently, there is a flat deformation of a layer in the plate towards , because there is no third dimension х, (along this one the pressure is not changed).

It is known that oscillations of plates of hard materials in this case are described by the equations of motion of thin plates in Lame form, but if the length of the track of a falling wave is no less than six of plate thickness:

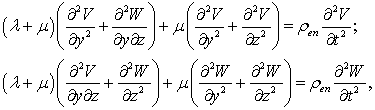(4)

where – stringing motions towards axes і ; – density of the layer of material; – by Lame constants

;

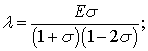
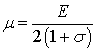Е – Young's modulus; – Poisson's ratio.

Acoustic pressure is written as the sum of symmetric and antisymmetric components –

and find out the ratio of their impact on forced oscillation of the plate "P".

Symmetrical components:

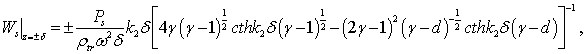
where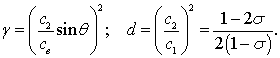

Antisymmetric component:

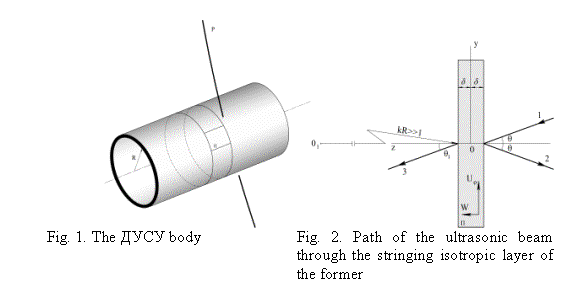
If we accept quantities as small і, then the function and can be substituted by the first two terms of the Taylor row, i.e., –

This will simplify the expressions:

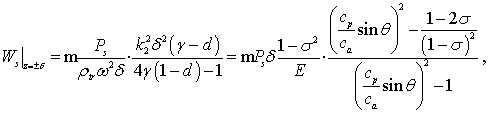(5)

where – the velocity of longitudinal (circumferential in the body) waves in the plate "P" for symmetric oscillations .

It is the same at the antisymmetric load if you accept that , we get –

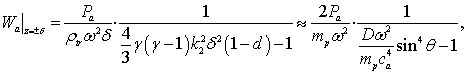(6)

where - cylindrical rigidity of the plate "P"; – specific weight.

The formula (6) is a well-known expression of conformity of bending oscillations of a thin plate.

Let us determine the scope of application of (6) hard and soft materials. A hard material is such a material in which the velocity circular (in formers) and transversal are larger than the sound speed in the air. The ДУСУ body is made of aluminum alloy, so let's assume it hard material, because for aluminum, .

Researches by Y.A. Nilender, E.S. Sorokin, Th. Kristen, H.W. Muller et al. proved that the Young's modulus E of hard materials, measured in dynamic and static modes, is not almost different in a wide frequency range. Therefore, it can be assumed that the velocity values and of wave propagation in circular direction (along the parallel of the body) in the transversal plane does not depend on frequency oscillations and they should be calculated by static measurements of Young's modulus and Poisson's ratio.

Thus, the oscillations of the obstacle made of a hard material under the action of a falling wave can be described by the equations of motion of thin plates, if the length of the track of a falling wave is no less than six times of the plate thickness, i.e.

.

Ratio of losses in hard materials is very small and can be considered as constant. Thus, for aluminum, the loss ratio at frequency is , and in a construction is about zero.