Листопадова В.В.

Національний технічний університет України «КПІ»

АНАЛІТИЧНЕ ВИЗНАЧЕННЯ МІСЦЕЗНАХОДЖЕННЯ РУХОМОГО ОБ’ЄКТУ В ПРОСТОРІ

Поняття про рух, так само як і поняття про спокій, за самою своєю суттю являється відносним. Отже, доходячи висновків щодо стану руху чи спокою твердого тіла, перш за все слід визначити предмет, відносно якого змінюється в часі (або не змінюється) положення цього тіла. При аналітичному описі руху за такий предмет обирається декартова система координат. Вибір її, власне кажучи, чиниться довільно. Обирається умовно нерухома (абсолютна) система відліку, осі якої позначимо .

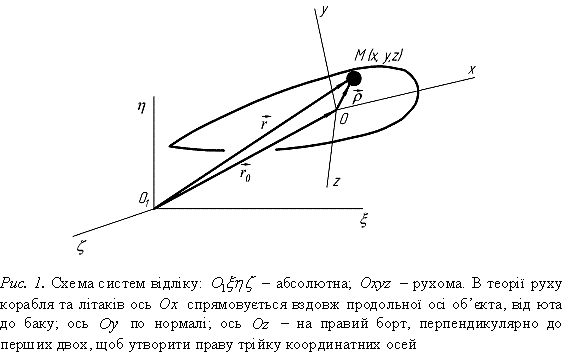
В рухомому тілі довільну точку О приймемо за початок системи координат , яку жорстко зв’яжемо з тілом (рис. 1). Цю систему координат будемо іменувати рухомою, або відносною. Природно, що координати будь-якої точки М тіла в рухомій системі будуть означеними і незмінними увесь час.

Положення рухомого об’єкту вважається визначеним, якщо відомі в довільний момент часу координати будь-якої його точки в абсолютній системі відліку. Якщо та – радіус-вектори полюса О і довільної точки М в опорній системі, а – радіус-вектор цієї точки відносно полюса О, тоді відповідно до рис.1 маємо очевидне співвідношення –

, (1)

де – орти рухомої системи координат.

Слід пам’ятати, що координати сталі за весь час руху. Тоді як одиничні вектори системи являються функціями часу (змінюється їх положення).

За обраної схеми, абсолютним рухом т. М об’єкту вважається її переміщення відносно абсолютної системи відліку , відносним – рух відносно рухомої системи . Переносним рухом іменується переміщення системи координат відносно абсолютної системи .

Очевидно, що одному векторному рівнянню (1) еквівалентні три скалярних –

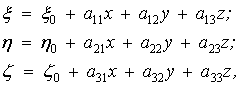(2)

де – напрямні косинуси і дорівнюють проекціям ортів на відповідні осі абсолютної системи координат .

Таким чином, мають місце дванадцять функцій часу:

координати полюса т. О – (3)

дев’ять напрямних косинусів –

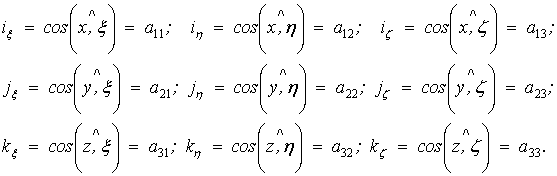(4)

Формули (2) являють собою загальні рівняння руху об’єкта. Вони безпосередньо подають координати будь-якої точки рухомого апарату у функції часу в абсолютній системі відліку. Координати полюса визначають поступальний рух об’єкту, напрямні косинуси окреслюють рух навколо полюса т. О.

Дев’ять напрямних косинусів не виявляються незалежними. Між ними існує певна кількість співвідношень. Перш за все, сума квадратів напрямних косинусів довільної прямої в декартовій системі координат дорівнює одиниці, тобто:

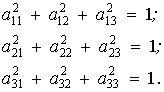(5)

Крім того, довільна пара осей рухомої системи взаємно перпендикулярна, тому очевидні рівності:

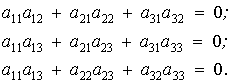(6)

Аналогічні міркування дають також наступне:

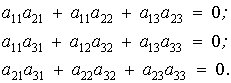(7)

Між дев’ятьма напрямними косинусами існує ще декілька співвідношень, однак незалежними будуть тільки шість, наприклад, (5), (6), або (5), (7). Отже, можна довільно задати тільки три напрямних косинуси, інші шість обчислюються із однієї з наведених систем. Вирази ці досить громіздкі.