Математика/4. Прикладная математика

К. ф.‑м. н. Карнаух Т.А.

КНУ им. Т. Шевченко, Украина

Построение возможностей и необходимостей

Решение задач распознавания можно свести к оценке возможности того, что расстояние от исследуемого объекта до образца не превышает некоторой малой величини. Этот подход формализуют понятия возможности, ультравозможности и необходимости для псевдометрического пространства [1, 2].

При задании возможностей часто достаточно задать значения в определенных точках. Поэтому актуальной становится задача пополнения частичной функции до возможности, ультравозможности и необходимости.

Введем несколько обозначений. Пусть запись f(x, y, t)¯ обозначает тот факт, что значение функции f в точке (x, y, t) определено. Для функции f:X´X´[0; +¥)®[0; 1] положим f_s = f È {((y, x, a), t) | ((x, y, a), t)Îf}.

Теорема 1 (пополнение функции до ультравозможности). Частичная функция f:X´X´[0; +¥)®[0; 1] может быть доопределена до ультравозможности в псевдометрическом пространстве (X, d) тогда и только тогда, когда она удовлетворяет условиям:

1) f_s является функцией (возможно, частичной), удовлетворяющей на области определения всем условиям, которые накладываются на ультравозможность;

2) если значение inf{f_s(x, y, t) | f_s(x, y, t)¯, t ³ d(x, y)} существует,  то равно 1.

Доказательство. (Þ) Пусть p — некоторое пополнение функции f до ультравозможности. Из симметричности возможности f_s Í p . Условия, которые накладываются на ультравозможность, должны выполняться для произвольного ее сужения. Докажем, что имеет место условие (2) теоремы. Пусть

inf{f_s(x, y, t) | f_s(x, y, t)¯, t ³ d(x, y)} < 1.

Тогда для некоторого a ³ d(x, y) выполнено f_s(x, y, a) < 1, а тогда и p(x, y, a) < 1. Из определения ультравозможности a < d(x, y). Противоречие.

(Ü) Докажем достаточность. Для x, yÎX введем в рассмотрение величины A, B, C, содержательно соответствующие значениям искомой ультравозможности p(x, y, ×) в точках 0, d(x, y) и на бесконечности. Если область определения функции f_s(x, y, ×) пуста, положим A = ½; иначе возьмем A = inf{ f_s(x, y, t) | f_s(x, y, t)¯}. Также положим B = C = 1.

Если область определения функции f_s(x, y, ×) неограничена, положим

H(x, y) = {((x, y, 0), A), ((x, y, d(x, y)), B)},

иначе возьмем произвольное D > d(x, y), ограничивающее область определения функции f_s(x, y, ×), и положим

H(x, y) = {((x, y, 0), A), ((x, y, d(x, y)), B)} È {((x, y, D + n), C)} | n ÎN₊}.

Соответствие h = f_s È функционально, монотонно относительно расстояния на области определения, h = h_s и удовлетворяет всем условиям теоремы. Для x, yÎX и a ³ 0 зададим значение p(x, y, a). Если значение h(x, y, a) определено, положим p(x, y, a) = h(x, y, a). Иначе

a‑ = sup{t| h(x, y, t)¯, tÎ[0; a)}, b‑ = sup{ h(x, y, t)| h(x, y, t)¯, tÎ[0; a)},

a₊ = inf {t| h(x, y, t)¯, tÎ(a; +¥)}, b₊ = inf{ h(x, y, t)| h(x, y, t)¯, tÎ(a; +¥)},

если a‑ = a₊, то p(x, y, a) = (b‑ + b₊)/2, иначе p(x, y, a) = .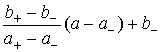

По построению f Í f_s Í h Í p, функция p монотонна относительно расстояния и для нее выполняется условие симметричности. По построению p(x, y, d(x, y)) = h(x, y, d(x, y)) = 1 и функция p –— ультравозможность.

Замечание. Можно привести примеры, когда доопределение функции до возможности (ультравозможности) можно сделать несколькими способами. В частности для пустой функции f можно построить бесконечно много расширений, являющихся возможностями и ультравозможностями в одномерном евклидовом пространстве.

Теорема 2 (пополнение функции до необходимости). Частичная функция f:X´X´[0; +¥)®[0; 1] может быть доопределена до необходимости в псевдометрическом пространстве (X, d) тогда и только тогда, когда она удовлетворяет таким требованиям:

1) f можно доопределить до возможности (см. теорему 7, [2]); 

2) sup{f_s(x, y, t) | f_s(x, y, t)¯, 0£ t £ a} = 1 Þ d(x, y) £ a.

Доказательство. (Þ) Первое условие вытекает из того, что необходимость должна быть возможностью. Проверим второе. Пусть n — некоторое пополнение функции f до необходимости. Из симметричности f_s Í n . Условия, накладывающиеся на необходимость, выполнены и для ее сужения.

Пусть для некоторых x, yÎX и a ³ 0 выполнено

sup{f_s(x, y, t) | f_s(x, y, t)¯, 0£ t £ a } = 1 .

Поскольку необходимость монотонна относительно расстояния, то

1 ³ n(x, y, sup{t | f_s(x, y, t)¯, 0£ t £ a}) ³  sup{n(x, y, t) | f_s(x, y, t)¯, 0£ t £ a} = 

= sup{ f_s(x, y, t) | f_s(x, y, t)¯, 0£ t £ a} = 1,

откуда n(x, y, sup{t | f_s(x, y, t)¯, 0£ t £ a}) = 1, но тогда

d(x, y) £ sup{t | f_s(x, y, t)¯, 0£ t £ a},

поскольку sup{t | f_s(x, y, t)¯, 0£ t £ a} £ a, то d(x, y) £ a.

(Ü) Для доказательства теоремы в части достаточности используем соответствующую часть доказательства предыдущей теоремы, сделав изменение: в случае неопределенного значения f_s(x, y, 0) положим

A = inf{ f_s(x, y, t) | f_s(x, y, t)¯}, если inf{ f_s(x, y, t) | f_s(x, y, t)¯} < 1;

A = ½, если inf{ f_s(x, y, t) | f_s(x, y, t)¯} = 1.

Докажем, что построенная с помощью так определенных A, B, C функция p будет еще и необходимостью. Для этого достаточно доказать, что из условия p(x, y, a) = 1 следует d(x, y) £ a.

Пусть p(x, y, a) = 1. Если h(x, y, a) определено, то p(x, y, a) = h(x, y, a) = 1. Поскольку множество H(x, y) не вводит значение возможности 1 для аргументов, меньших расстояния, то f_s(x, y, a) = 1 и d(x, y) £ a из условия теоремы. Докажем, что при неопределенном значении h(x, y, a) также выполнено d(x, y) £ a. Пусть a < d(x, y). Если значение h(x, y, a) неопределено, то неопределено и значение f_s(x, y, t), а потому

a‑ = sup{t| h(x, y, t)¯, tÎ[0; a)} = sup{t| h(x, y, t)¯, tÎ[0; a]},

b‑ = sup{ h(x, y, t)| h(x, y, t)¯, tÎ[0; a)} = sup{ h(x, y, t)| h(x, y, t)¯, tÎ[0; a]}.

Если множество {t| f_s(x, y, t)¯, tÎ[0; a]} пусто, то b‑ = A < 1; иначе

b‑ = sup{ h(x, y, t)| h(x, y, t)¯, tÎ[0; a]} = sup{ f_s(x, y, t)| h(x, y, t)¯, tÎ[0; a]} < 1

по условию теоремы, поскольку по предположению a < d(x, y).

В обоих случаях (b‑ + b₊)/2 < 1, поэтому значение p(x, y, a) определялось по формуле p(x, y, a) = 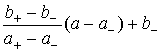. Поскольку b‑ £ b₊ £ 1, то равенство p(x, y, a) = 1 возможно лишь при условии a = a₊, b₊ = 1, т.е. a₊ = inf {t| h(x, y, t)¯, tÎ(a; +¥)}, b₊ = inf{h(x, y, t)| h(x, y, t)¯, tÎ(a; +¥)} = 1.

Тогда существует монотонно убывающая и сходящаяся к a последовательность (a_n)_nÎN, такая что для всех nÎN функция f_s(x, y, ×) определена в точке a_n и a_nÎ[a; d(x, y)). Из свойств инфинума необходимо f_s(x, y, a_n) ³ 1, откуда d(x, y) £ a_n. Получено противоречие, поскольку a < d(x, y) при p(x, y, a) = 1 невозможно. Теорема доказана.

Литература:

1. Карнаух Т.О. Відстані в синтаксичних просторах / Т.О. Карнаух // Вісник Київського національного університету імені Тараса Шевченка. Серія: фіз.-мат. науки. – 2012. – Вип. 2. – С. 134-139.

2. Карнаух Т.О. Метрично-можливісний підхід до задач розпізнавання / Т.О. Карнаух // Вісник Київського національного університету імені Тараса Шевченка. Серія: фіз.-мат. науки. – 2012. – Вип. 3. – С. 167-172.