Некоторые алгоритмы исследования

динамических систем (из опыта применения)

Гарькина И.А., Данилов А.М.

Пензенский государственный университет архитектуры и строительства

В настоящее время при исследовании и проектировании систем управления используется информация о динамических характеристиках объектов сигналов, не обязательно являющаяся необходимой для управления. Нередко возникает вопрос, является ли современная теория процессов управления подходящим инструментом для исследования и проектирования систем управления. Во время войны известными летчиками стали выпускники летных школ, не имеющие ни малейшего представления о дифференциальных уравнениях вообще, не то, что о дифференциальных уравнениях, которыми описывается движение летательного аппарата. Напомним и известное замечание в [1] о езде мальчика на велосипеде, не имеющего представления ни о площади опоры, скорости, ускорении и т.д., которые фигурируют в системе дифференциальных уравнений, описывающих движение велосипедиста. Большинство исследователей, анализируя деятельность человека-оператора, рассматривают ее как ряд последовательно выполняемых действий. Это вытекает из предположений, что механизм переработки информации человека функционирует как одноканальная система. Однако допускается и возможность одновременного выполнения нескольких действий, что основывается на предположении, что механизм приема и обработки информации человека представляет собой многоуровневую иерархическую систему.

Все это требует разработки новых методов теории управления, в том числе для повышения эффективности математического моделирования динамических систем.

Несмотря на имеющиеся недостатки, на практике удовлетворительные результаты можно получить при использовании нижеприводимых алгоритмов.

Статистический анализ данных

1. Анализ корреляционных полей (графическое отображение взаимозависимости двух факторов: эмпирическая, теоретическая линии регрессии, определение уровней значимости) [2].

2. Проверка нормальности закона распределения.

Должно выполняться ; ,

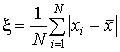-среднеарифметическое значение параметра,

- текущее значение параметра,

- среднеарифметическое отклонение параметра от среднего по абсолютной величине.

Такая проверка возможна по асимметрии и эксцессу.

3. Проверка воспроизводимости процесса по Кохрену .

4. Проверка стационарности процесса по:

- F-критерию, ;

- колебательному критерию.

Выбор вида зависимостей

1. Предварительное определение типа зависимостей.

2. Установление характера зависимостей по коэффициенту корреляции и корреляционному отношению

; ; ;

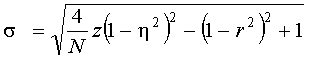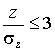- показатель нелинейности связи, - корреляционное отношение, - коэффициент корреляции.

Получение количественных зависимостей

по методу множественной регрессии

1. Линейная регрессия.

2. Нелинейная регрессия.

3. Проверка точности уравнения регрессии по доверительному интервалу.

4. Окончательный отсев несущественных параметров по невязкам.

5. Проверка адекватности уравнения регрессии:

- по ошибке аппроксимации ,;

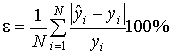- ошибка аппроксимации, - значение зависимой переменной, рассчитанной по уравнению регрессии, - значение зависимой переменной, полученной опытным путем;

- по -критерию [3].

6. Уточнение уравнений регрессии.

В случае нестационарных процессов коэффициенты регрессии изменяются во времени и их надо периодически обновлять (например, путем обработки новых опытных данных).

Отсев несущественных параметров зависимостей процесса

1. По данным парного корреляционного анализа.

2. По методу ранговой корреляции [4].

3. По данным множественного корреляционного анализа.

4. По сводному коэффициенту корреляции.

Приведенные алгоритмы успешно использовались при разработке тренажеров мобильных систем, моделировании композитов и др.

Литература

1. Эйкхофф П. Основы идентификации систем управления. - М.: Мир, 1975. - 680 с.

2. Лившиц Н.А., Пугачев В.Н. Вероятностный анализ систем автоматического управления. В 2-х томах. – М.: - Советское Радио, 1963. - т.1 – 896 с., т.2 – 484 с.

3. Фишер Р.А. Статистические методы для исследователей. Пер. с англ. – М.: Госстатиздат. 1958. - 267 с.

4. Юл Дж.Эдни, Кенделл Дж.М. Теория статистики. Пер. с англ. Под ред. Ф. Д. Лившица. - 14-е изд., пересмотр. и расшир. - Москва: Госстатиздат, 1960. - 779 с.