Педагогические
науки/5. Современные методы преподавания
Магистр Артеменко Н.М.
Юго-западный государственный университет, Россия
АРХИКАЛЬКУЛЯТОР
В настоящее время существует множество
различных программных и аппаратных разработок калькуляторов. Например: калькулятор выражений и конвертер
единиц измерения со скинами и множеством дополнительных возможностей со
стандартным калькулятором Windows [1]; 2х2 калькулятор для выполнения инженерных или бухгалтерских
расчетов [2]; «продвинутый»
калькулятор Calc: конвертер
физических единиц; калькулятор дат и конвертер календарей и универсальный
решатель алгебраических уравнений [3]; мульти-платформенный Flash Калькулятор
1.0,[4] и т.п.. Однако, указанные
калькуляторы не предназначены для обучающих целей и не несут в себе
«познавательную историю», необходимую
при изучении «информатики» в средней и
высших школах.
Таким
образом, целью исследования являлась разработка калькулятора, позволяющего
отображать информацию и выполнять
арифметические операции в типовых, так и не используемых в настоящее время
системах счисления, с предоставлением консультационной помощи.
На
первом этапе исследований были изучены различные системы исчисления,
исторически возникшие в процессе интеллектуального развития человечества (древне
шумерская – 4-6 тысячетелитие до нашей эры, жрецов майя – 1-2 века нашей эры,
римская, традиционная арабская) и интерфейсные части представленных в интернет сети калькуляторов.В
качестве платформы реализации калькулятора выбрана операционная система Windows XP, в
качестве языка программирования – Java [5].
Разработанный
калькулятор позволяет: в десятичной системе производить арифметические и
алгебраические действия со скобками и без, запоминать промежуточный результат,
представлять числа в градусах и радианах;
представлять числа в любой иной задаваемой системы исчисления с
целым основанием, работать с числами представленными в римской, майеской и
шумерской системах счисления;
Рассмотрим
более подробно нестандартные системы исчисления, применяемые в предлагаемом
калькуляторе.
Система счисления жрецов Майя [6]. Майя
записывали цифры в виде точек и тире. Причем точка всегда означала единицы данного порядка, а тире –
пятерки. Цифры располагались по вертикали (может быть, «навеено» шумерской
системой исчисления). По сути, это был пятерично двоичный код, изобретенный в первые века нашей эры
(«пять пальцев – две руки»)..
Майя использовали следующие коды цифр:
1 - ![]() : 2 -
: 2 - ![]() : 3 -
: 3 - ![]() : 4 -
: 4 - ![]() ;
;
5 - ![]() ;6 -
;6 - ![]()
![]() ; 7 -
; 7 - ![]() ; 8 -
; 8 - ![]() : 9 -
: 9 - ![]() ;
;
10 - ![]() ; 11 -
; 11 -![]() ; 12 -
; 12 - ![]()
![]() ; 13 -
; 13 - ![]() : 14 -
: 14 - ![]() ;
;
15 - ![]() ; 16 -
; 16 - ![]() ; 17 -
; 17 - ![]() ; 18 -
; 18 - ![]() ; 19 -
; 19 - ![]() .
.
У Майя
десятичный эквивалент числа 20 означает переход на новый разряд («двадцатеричная»
система счисления, позволяющая емко представлять большие числа). Для
представления «0» жрецы использовали изображение символа лежащей на боку
раковины («![]() »). Чтобы изобразить число 20 жрецы переходили на новую «полку».
Число «20» обозначалось как
»). Чтобы изобразить число 20 жрецы переходили на новую «полку».
Число «20» обозначалось как ![]() .
.
Поскольку
любая система исчисления изобреталась для решения практических нужд, то и майя «нарушили»
построение позиционной системы (но только один раз), «привязав» ее к календарю.
Это позволило им «отсекать» годичные циклы. Поскольку математические расчеты у
жрецов майя были в основном связаны с астрономическими вычислениями, они
максимально приблизили первоначальное число третьего порядка к числу дней года,
поскольку в 18 двадцатидневных месяцах, составляющих календарный год майя число
дней равно 360.
Хронологически
«отойдем» на несколько тысячателетий назад: Древний Шумер и его система
счисления [7]. В отличии от современной десятичной системы
исчисления шумерская была шестидесятеричной. Причем, позиционность кода в
данном случае интересная. За основание системы исчисления вначале берется 60, в
следующем разряде оно заменяется на 10, затем снова на 60 и т.д. Т.е.,
позиционные числа выстраиваются в следующий ряд: 1, 10, 60, 600, 3600, 216000,
2160000, 12960000 и т.д. Такая система позволяла шумерам вычислять дроби,
перемножать числа и извлекать корни.
Заметим, что эта система несколько лучше десятичной – например, число 60
имеет десять простых делителей, а 100 – всего 7. У древних майе это
превосходство еще нагляднее. Шумеры
пользовались клинописью и высекали изображения чисел и звуков на глиняных
«кирпичах». Например, таким [8] –
Рисунок 6.
Кодирование
числовой (т.е. предназначенной для измерения информации) предлагается следующим
– Таблица 1. Заметим, что представленные «клинописные знаки» легко получаются
на камне с помощью «зубила и молотка» или на невысохшей глине.
Таблица 1
Кодирование чисел шумерами
|
Десятичный эквивалент |
клинопись |
|
0 |
▲ – «ракушка» |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
Программа
построена по модульному принципу, что позволяет достаточно оперативно и просто
модифицировать ее при необходимости.
Литература
1.
Сайт http://www.romanlab.com
2.
Сайт http://www.pautinka.net/~calc2x2/
3.
Сайт http://thecalc.narod.ru/
4.
Сайт http://calc.ztor.com/
5.
Программирование на Java / Вязовик Н.А. /М.:
ИНТУИТ.РУ, 2003. -592 с.
6.
Кузьмичев В.А. Тайна жрецов майя. / - М.: Ид «Флюид», 2006. - 352 с.
7. Клейменов Г. Н. Ануннаки: Творцы жизни на Земле и
учителя человечества. Исследование мифов, легенд и летописей. – М.: КомКнига,
2006. – 344 с.
8.
Ситчин З. Назад в будущее. – М. Эксмо, 2007. – 416 с.
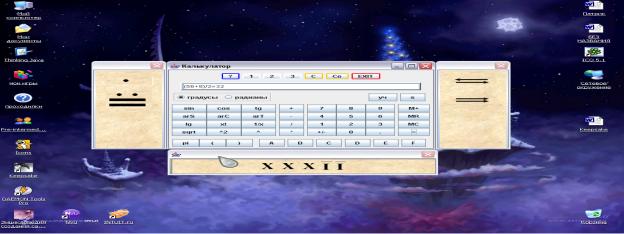
Рисунок 1
Основной (многофункциональный) интерфейс калькулятора
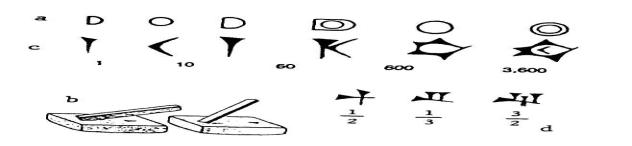
Рисунок 2 Клинопись чисел в древнем Шумере (согласно
[7])