Гончарук В.В.

Національний авіаційний університет, Україна

Моделювання псевдовипадкової послідовності з заданою кореляційною функцією в системах електропостачання

При імовірнісному моделюванні процесів в системах електропостачання іноді виникають труднощі з отриманням аналітичних виразів для числових характеристик або законів розподілу досліджуваних показників. Труднощі можуть бути пов'язані з великою розмірністю задачі корельованості або з нелінійними залежностями між змінними, що впливають на досліджуваний процес. У цьому випадку виходом з положення може бути використання методів імітаційного моделювання (ІМ) [1]. У дослідженнях електричних навантажень, властивості електроенергії та інших показників методи імітаційного моделювання почали використовуватися з розвитком засобів обчислювальної техніки [3]. Завдання моделювання псевдовипадкової послідовності (ПВП) із заданою кореляційною функцією (КФ) виникає при імітаційному моделюванні об'єктів або процесів коли необхідно врахувати не тільки закони розподілу випадкових величин або процесів, а й кореляційні функції або спектральні щільності модельованих реалізацій.

Для моделювання ПВП із заданою КФ у вигляді аналітичного виразу (експоненціальна, трикутна або експоненціально - косинусна та ін..) можна скористатися методом викладеним в [5], суть якого полягає в перетворенні сигналу , що є білим шумом, в сигнал із заданою відповідно до передавальної функції

.

Для заданого аналітичного виразу КФ модельованого сигналу визначається двостороннє дискретне перетворення Лапласа або - перетворення гратчастої КФ одержуваної з вихідної безперервної КФ [2]

. (1)

Далі вираз для представляється у вигляді добутку наступним чином:

, (2)

де - - перетворення передавальної функції гратчастої функції . Дискретну передавальну функцію необхідно представити у вигляді дробу:

, (3)

де , - - перетворення гратчастих входу і виходу сигналів деякої дискретної системи автоматичного управління (САУ) [5].

За допомогою зворотного - перетворення можна отримати наступний рекурентний вираз для моделювання послідовності (вихід) по вихідної послідовності (вхід), що має властивості білого шуму [1]:

, (4)

де - вагові коефіцієнти.

Для експоненційної КФ виду [2]

(5)

рекурентна послідовність (4) може бути отримана в загальному вигляді. Представимо у вигляді гратчастої функції наступним чином [5]:, де - інтервал дискретності гратчастої ;.

Пряме і обернене дискретні -перетворення Лапласа будуть мати вигляд [2]: ; .

З урахуванням того, що , вираз (1) і (2) для  можна записати наступним чином:

;

.

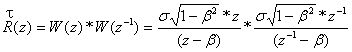Представлення у вигляді дробу (3) буде виглядати наступним чином:

.

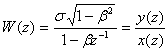Отже, рекурентний вираз (3) для випадкової послідовності з (5) має вигляд [5]:

, (6)

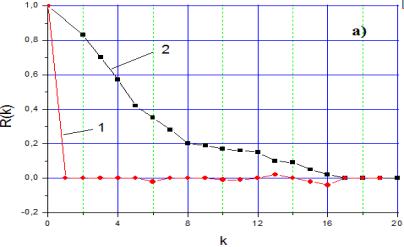
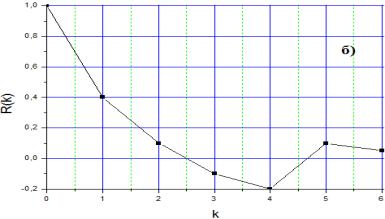
Рис.1. а) кореляційні функції: 1- моделі білого шуму ;

2- модельованої послідовності . ;б) моделювання випадкового графіка навантаження з кореляційною функцією, заданою в точках білого шуму, тобто, її кореляційна функція близька нулю у всіх точках, крім .

Даний рекурентний вираз може бути використано для моделювання на ЕОМ псевдовипадкової послідовності з виду (5). Для цього в якості необхідно використовувати випадкову послідовність, що має властивості білого шуму [1].

На рис. 1 показаний приклад моделювання на ПЕОМ ПВП із заданою , у якої кВт, = 0,1 1/хв, хв. В якості вхідного білого шуму використовувалася ПВП з рівномірним законом розподілу на інтервалі [0,1], отримана за допомогою процедури Random алгоритмічної мови Mathcad, перетворена в модель ПВП з нормальним законом розподілу наступним чином [3]: , де - ПВП, рівномірно розподілена на інтервалі [0,1] з дисперсією . Отримана, таким чином, ПВП має розподіл близький до нормального та .

Метод імітаційного моделювання, будучи в значній мірі універсальним, проте не може замінити повністю аналітичні методи отримання законів розподілу випадкових величин і процесів. Володіння аналітичним законом дає більше можливостей для узагальнень і для виявлення окремих випадків, тобто аналітичні методи дають більше інформації для подальшого розвитку теорії.

Література:

1. Бусленко В.Н. Автоматизация имитационного моделирования сложных систем. - М.: Наука, 1977.-240с.

2. Деч Г. Руководство к практическому применению преобразования Лапласа и Z- преобразования,- М.: Наука, 1971. - 288с.

3. Куренный Э.Г., Брусенцов Л.В. Моделирование групповых графиков электрической нагрузки методом Монте-Карло. - Изв. вузов Сер. Электромеханика, 1968, N 7, с.788-792.

4. Надтока И.И. Нормирование, контроль и управление электропотреблением в АСУ энергетического хозяйства предприятия. /Электрические нагрузки и электропотребление в новых условиях хозяйствования. Материалы семинара. -М.:1989. -С.133-136.

5. Цифровое моделирование систем стационарных случайных процессов /Гридина Е.Г., Лебедев А.Н., Недосекин Д.Д., Чернявский Е.А. - Л.:Энергоатомиздат, 1991. - 144с.