Технические науки / 5. Энергетика

Поляхов Н.Д., Приходько И.А., Швыров И.В.

Санкт-Петербургский Государственный Электротехнический Университет («ЛЭТИ»)

ОПТИМАЛЬНОЕ РАЗМЕЩЕНИЕ УСТРОЙСТВ FACTS В ЭЛЕКТРОТЕХНИЧЕСКОЙ СИСТЕМЕ С ПОМОЩЬЮ ЭВОЛЮЦИОННЫХ АЛГОРИТМОВ

В современной электроэнергетике особое место занимают, так называемые устройства FACTS (Flexible AC Transmission Systems) или гибкие системы передачи переменного тока (в языке отечественных энергетиков чаще встречается термин «устройства управления передачей электроэнергии»). В связи с повышенным интересом к развитию «интеллектуальной энергетики» не только в нашей стране, но и во всем мире применение таких устройств становится особенно актуальным. Основная функция их заключается в возможности «гибкого» управления режимами в реальном времени: поддержания необходимого уровня напряжения в сети, управления потоками мощности, повышения пропускной способности ЛЭП, повышения статической и динамической устойчивости ЭЭС.

Устройства управления передачей электроэнергии можно разделить по их назначению и исполнению на несколько групп:

- устройства компенсации реактивной мощности (для параллельного подключения в сети);

- устройства регулирования параметров сети (для последовательного включения в сети);

- комбинированные устройства, включающие функции первых двух групп (продольно-поперечного включения).

В задачах оптимизации режима по реактивной мощности заранее известны места установки КУ и требуется определить только их оптимальные значения мощности для конкретного случая. При проектировании и развитии ЭЭС рассматриваются задачи определения оптимальных мощностей и мест установки КУ.

Вольтодобавочные устройства(ВДУ) создают добавочное напряжение, которое может совпадать или не совпадать по фазе с основным напряжением. В зависимости от этого ВДУ подразделяются на устройства с продольным или поперечным регулированием(линейные регуляторы). В задачах проектирования, так же как и с КУ, требуется определение оптимальных параметров и мест установки ВДТ.

В задачах оптимального выбора параметров и мест установки электротехнических устройств приходится сталкиваться с дискретными значениями переменных, соответствующих как точкам установки устройств в системе, так и регулируемыми параметрам, что приводит к усложнению процесса оптимизации(что определяет применение эволюционных алгоритмов).

Эволюционные алгоритмы(ЭА) – направление в искусственном интеллекте, которое использует и моделирует процессы естественного отбора[1].

При поиске экстремума на первом шаге происходит случайная генерация в области допустимых значений возможных решений, которые соответствуют некоторому значению целевой функции. На следующем шаге выбираются наиболее подходящие (в зависимости от значения целевой функции) решения, вблизи которых определенным способом выделяются «перспективные» решения для дальнейшего их рассмотрения и участия в процессе поиска оптимальных решений. Выбор наиболее подходящих решений(точек) соответствует естественному отбору(селекции) в реальной природе.

Среди особенностей ЭА можно отметить следующие:

1. ЭА – поисковые алгоритмы стохастической оптимизации, которые не гарантируют нахождения точного решения, но тем не менее с их помощью можно «достаточно быстро и достаточно точно» найти решение.

2. На каждой итерации оперируют с совокупностью решений.

3. Не требуют каких-либо дополнительных ограничений для оптимизируемой функции (непрерывность, дифференцируемость). Что является особенно важным для решения практических(реальных) задач.

4. В зависимости от условий задачи, приведенные алгоритмы можно настраивать, например по точности или скорости выполнения. На это влияет набор определенных параметров для каждого алгоритма.

Формулировка задачи определения оптимальных параметров и мест установки устройств FACTS:

- Минимизировать целевую функцию, представляющую собой суммарные потери активной мощности в ЭЭС:

В случае размещения КУ: ,

где - вектор значений реактивных мощностей КУ.

В случае размещения ЛР: ,

где - вектор значений углов ЛР.

- Учитывая ограничения в виде равенств, представляющие собой УУР:

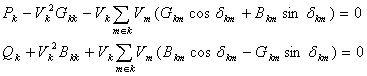
где - модуль и фазовый угол комплекса напряжения, активная и реактивная мощности узла k ; – элемент матрицы комплекса узловых проводимостей; – разность фазовых углов между смежными узлами k и m.

- Учитывая ограничения в виде неравенств, представляющие собой предельные ограничения на следующие переменные: реактивные мощности компенсирующих устройств или значения углов линейных регуляторов, модули и фазовые углы комплекса напряжений.

Необходимо отметить, что при такой формулировке задачи не учитываются такие важные критерии, как затраты на приобретение необходимых устройств и затраты на их обслуживание. Целью данной задачи является исследование влияния КУ на параметры режима в ЭЭС.

Обобщенный алгоритм для поиска оптимальных мощностей или фазовых углов (в зависимости от вида задачи) и мест установки КУ (или ЛР) в ЭЭС. Поскольку расчетная часть не изменяется, а с помощью ЭА образуется циклический процесс, укрупненный обобщающий алгоритм выглядит следующим образом:

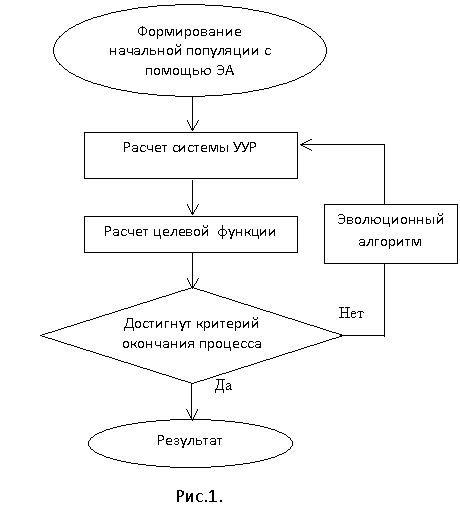
Шаг 1: Случайным образом в интервале допустимых значений формируется начальная популяция, представляющая собой совокупность индивидуумов, которые соответствуют возможным решениям задачи(в зависимости от вида задачи).

Шаг 2: Производится расчет системы нелинейных уравнений установившегося режима методом Ньютона.

После расчета системы происходит проверка ограничений, наложенных на переменные(в зависимости от вида задачи) с помощью метода штрафов.

Шаг 3: Расчет целевой функции - суммарных потерь в энергосистеме:

,

Шаг 4: Проверка критерия остановки процесса оптимизации. Если выполнено заданное количество итераций для ЭА, то алгоритм прекращает работу и будет выбран режим, для которого значение целевой функции имеет наилучшее значение, и параметры которого удовлетворяют заданным требованиям, в противном случае переходит к выполнению шага 5.

Шаг 5: С помощью ЭА формируется новая популяция, соответствующая новым решениям задачи.

Далее алгоритм переходит на Шаг 2 и так далее, пока не сработает критерий остановки в виде заданного количества итераций.

Будем рассматривать задачу оптимального размещения КУ(ЛР) на примере стандартной 30-узловой схемы IEEE (Institute of Electric and Electronic Engineers)[2]. В качестве исходных данных будем использовать результаты расчета режима по активной мощности[3], то есть все активные мощности генераторных станций кроме балансирующей фиксированы.

В представленной ЭЭС имеется 6 тепловых электростанций (ТЭС) – узлы 1,2,5,8,11,13, а также 24 нагрузочные станции. Имеется 5 КУ(ЛР) с пределами регулирования реактивной мощности от 0 до 10 МВар (-5 до 5 градусов), требуется найти такие места размещения КУ(ЛР) и их параметры, чтобы суммарные потери активной мощности в сети были минимальными.

Сравнительные результаты расчетов оптимального размещения КУ(ЛР) в ЭЭС с помощью эволюционных алгоритмов(генетического (ГА), пчелиного (ПА, муравьиного алгоритмов (МА)) представлены в табл. 1.

Таблица 1

	Метод расчета
	ГА				ПА				МА
	№узла		Q,МВар		№узла		Q,МВар		№узла		Q,МВар
КУ1	4		10		6		9,99		4		9,62
КУ2	6		10		7		9,98		7		9,95
КУ3	7		10		15		6,30		18		4,26
КУ4	21		9,77		17		8,30		21		9,49
КУ5	24		8,11		24		9,02		24		8,05
Потери, МВт	9,29				9,31				9,30
	Метод расчета
	ГА			ПА				МА
	Ветвь	,град		Ветвь		,град		Ветвь		,град
ЛР1	6-9	-3		6-9		-3		6-9		-3
ЛР2	6-10	5		6-10		5		6-10		5
ЛР3	9-10	-4		9-10		-4		9-10		-4
ЛР4	27-29	1		27-29		1		27-29		1
ЛР5	27-28	1		27-28		1		27-28		1
Потери, МВт	9,32			9,32				9,32

При использовании ЭА для оптимального размещения КУ и ЛР в ЭЭС удалось снизить потери активной мощности на 3,5%.

Литература:

1. Королев Л.Н.,«Эволюционные вычисления, нейросети,генетические алгоритмы – формальные постановки задач», Фундаментальная и прикладная математика, 2009.

2. http://shodhganga.inflibnet.ac.in/bitstream/10603/1271/18/18_appendix.pdf

3. Поляхов Н.Д.,Приходько И.А.,Швыров И.В., «Оптимизация распределения потоков мощности в энергосистеме с помощью генетических алгоритмов», Известия ЛЭТИ, 2012г.