Современные информационные технологии/1. Компьютерная инженерия

Вяткин С.И., Романюк^* С.А., Полищук^* А.В.

Институт автоматики и электрометрии СО РАН

. ^*Винницкий национальный технический университет

Особенности анимации трехмерных объектов с применением итерационных методов

Отдельным классом задач компьютерной графики является анимация персонажей трехмерной сцены, в которой возникает задача инверсной кинематики. При использовании инверсной кинематики не требуется анимировать каждый отдельный узел иерархически связной цепи, чтобы получить ее движение в целом. Если перемещать в пространстве туловище (родительский объект), вместе с ним, как жестко закрепленные, будут перемещаться руки, ноги и голова (дочерние объекты) – это цепь прямой кинематики, где воздействие на родительский объект влияет на его дочерние объекты. Если же в этом биподе реализована цепь обратной кинематики, то перемещение в пространстве дочернего объекта, например, кисти руки, приведёт к перемещению родительских объектов: предплечья, плеча, туловища. Каждый объект имеет свою локальную систему координат и характеризуется шестью степенями свободы: углы поворота вокруг осей координат и сами координаты. Все это можно описать одной матрицей в 3*4 элемента: первые три столбца характеризуют ориентацию (поворот) объекта, четвертый столбец – положение объекта. Вложив локальные системы координат объектов, друг в друга, т.е. связав их в иерархическую цепочку, получаем возможность вычислять глобальные координаты объектов.

Суть итерационных методов заключается в том, что решение достигается в ходе итерационного приближения. Основные проблемы, возникающие при этом – это сходимость таких методов. Большая часть итерационных методов основаны на алгоритмах численной минимизации нелинейной функции, есть алгоритмы, где используется геометрический подход.

Методы характеризуются средним количеством итераций, средним количеством вызовов функций за один полный проход алгоритма, средним временем одного полного прохода алгоритма, а также качественным параметром, характеризующим на сколько метод и визуальный эффект удовлетворяют ожидаемым результатам.

Главное для инверсной кинематики это быстродействие и точность решения. Наиболее существенной и труднорешаемой проблемой является проблема достижения заданной точности.

Теоретические основы методов не дают гарантий глобальной сходимости, так как итерационные методы относятся к методам поиска локального экстремума, а не глобального. Условием глобальной сходимости является монотонность взятой функции на всей области определения. В случае инверсной кинематики, вид функции неочевиден, особенно при большом количестве переменных. Это и есть основная теоретическая проблема таких методов. Вторая проблема – это точность. В отличие от реального мира, виртуальный мир имеет конечную точность, что неизбежно ведет к погрешностям вычисления, как значений функций, так и их производных.

Теоретические вопросы подобного рода трудно разрешимы и относятся к разряду фундаментальных проблем. Относительно вида функции инверсной кинематики (IK функции) можно сказать следующее. Из геометрии цепочки видно, что глобальному минимуму соответствует множество векторов из области определения, при этом существует проблема монотонности функции. В работе [1] показаны расширенная функция Розенброка, расширенная обобщенная функция Пауэла, функция типа спиралевидного желоба и функция Вуда. И если метод успешно справляется с минимизацией функции Вуда, всё равно нет гарантий, что на другой тестовой функции найдется решение. В связи с этим, единственный путь, хоть сколько-нибудь гарантирующий корректную работу метода для произвольной функции – это испытание его на как можно большем множестве нелинейных функций с глобальным минимумом. Только испытав метод на всех предложенных в [1] функциях, можно задаться достаточной долей уверенности в корректной работе метода для произвольной функции.

Кроме успешной работы метода, требуется качественно реализовать вычисление самой функции и ее производных. В отличие от тестовых функций, имеющих аналитический вид, IK функция такого вида не имеет, что существенно уменьшает точность вычисления производной по конечным разностям. Таким образом, не менее существенной проблемой, чем реализация метода, имеется проблема точного вычисления производных, в условиях значительной потери точности при вычислении функции. Для этих целей может использоваться метод Хемминга [2]. Ярким примером, насколько важно уметь правильно вычислять производную по конечным разностям, является все та же функция Вуда. IK–функция так же требует подбора оптимальных параметров для алгоритма.

Существуют несколько методов улучшающих эффективность итерационных подходов. Это переход от алгоритма BFGS к его модификации L-BFGS [3],[4], которая может существенно улучшить скорость работы алгоритма для большого количества переменных [5], [6]. Переход обычного алгоритма линейного поиска к алгоритму линейного поиска с условием на производную [7]. Переход от алгоритма обычного выбора шага при пересчете частных произвольных функций, к динамическому выбору шага. Переход от однопроходного алгоритма к многопроходному, с динамическим анализом выработки решения и с ограничениями на общее количество итераций

Следует также заметить, что линейный поиск с условием на производную в целом улучшает сходимость алгоритма на тестовых функциях, но не влияет на сходимость IK – функции. Большая часть затрачиваемого времени приходится на окрестность, где текущее значение целевой функции близко к желаемому значению, но еще не достигло желаемой точности. Теоретически, алгоритм BFGS имеет два основных терминальных кода (код завершения):

· относительный градиент функции меньше допустимого значения:

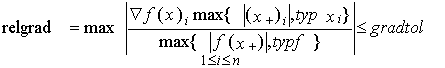
· относительное изменение последовательных значений вектора переменных меньше допустимого значения:

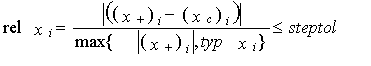
В работе [7] предлагается однопроходный вариант алгоритма, где он завершает свою работу по одному из вышеуказанных терминальных кодов. На практике это не дает желаемого результата, так как алгоритм завершает работу, не достигнув заданной точности. Анализ тестов показал, что так происходит потому, что обновляемая на каждом шаге матрица Гесса, которая призвана сохранять в себе информацию о предыдущей кривизне функции, ухудшает выбор направления спуска. Это вызвано тем, что всегда есть масса погрешностей в вычислении производных функций, которые после нескольких итераций могут ухудшить приближение матрицы Гесса. Поэтому лучше периодически приравнивать единице матрицу Гесса, что, по сути, равносильно новому запуску алгоритма. То есть, необходим многопроходный алгоритм.

Основная трудность, как уже упоминалось выше, заключается в том, что невозможно полностью протестировать до конца случаи работы алгоритма. В частности, при минимизации целевой функции в задаче IK, на каждом кадре задается некоторый начальный вектор, на нем высчитывается целевая функция и далее она минимизируется, тем самым, приводя цепочку IK - объектов в движение. При этом видно, что отображаемая IK – цепочка объектов двигается неравномерно, часто не достигая поставленной цели. Это значит, что на некоторых кадрах алгоритм не укладывается в указанную точность, завершая работу на значениях целевой функции вне допустимой точностью окрестности.

Литература

1. Дэннис Дж.. Численные методы безусловной оптимизации и решения нелинейных уравнений. Пер. с англ. Монография / Дж. Дэннис. – «Мир», 1988. – 157 с.

2. Хемминг Р. В. Численные методы для научных работников и инженеров /. Р. В. Хемминг. – М.: Наука, Физматлит, 1972. – 400 c.

3. Richard H. Byrd, Jorge Nocedal and Ciyou Zhu “Towards a Discrete Newton Method with Memory for Large Scale Optimization”/Di Pillo, Gianni (ed.) et al., Nonlinear optimization and applications. Proceedings of the 21st workshop, Erice, Italy, June 13-21, 1995. New York, NY: Plenum Press. 1-12 (1996).

4. Ciyou Zhu, Richard H. Byrd, Peihuang Lu and Jorge Nocedal. L-BFGS-B: Fortran Subroutines for large-scale bound constrained optimization. SIAM Journal on Physical Review B, 53(4):1740-1743, 1996.

5. D.C. Liu and J.Nocedal, “On the limited memory BFGS method for large scale optimization methods”, Mathemitical Programming 45 (1989), pp. 503-528.

6. J.Nocedal, “Updating quasi-Newton matrices with limited storage”, Mathematics of Computation 35 (1980), pp. 773-782.

7. Kwan W. Chin “Closed-form and generalized Inverse Kinematics solutions for animating the human articulated structure”. 1996.