Математика/4.Прикладная математика

К.ф.-м.н. Данилович Л.А., Концевой М.Г., д.ф.-м.н. Плетнев Л.В., Самосадов А.А.

Белорусско-Российский университет, г. Могилев, Республика Беларусь

Свойства величин определителей

Изучения курса высшей математики студентами, в современных условиях, требует интенсификации самостоятельного изучения различных разделов математики одновременно. В результате решения сложных задач, студенты, с синергетической точки зрения, начинают более глубоко понимать взаимосвязь различных разделов математики.

Одной из таких задач является задача о вычислении величин определителей и их распределении. Определители являются одними из простейших структур в математике, идея введения которых принадлежит Лейбницу, который опубликовал первое исследование, посвященное определителям в 1678 г. [1]. На протяжении двух столетий свойства определителей и матриц изучали Крамер, Вандермонд, Гаусс, Коши, Бине, Кэли, Сильвестр, Кронекер, Вейерштрасс. Широко определители используются в современной математике и физике [2,3].

Для изучения различных разделов математики, использования некоторых разделов математической статистики, прикладной математики и математического моделирования была поставлена задача о получении распределений величин всех определителей третьего порядка, элементы которых являлись различными цифрами от 1 до 9. С помощью комбинаторики, используя перестановки из 9 элементов (различных цифр), можно подсчитать число всех возможных определителей третьего порядка N = 9! = 362880.

Для анализа полученного распределения величин определителей были поставлены следующие задачи: сколько определителей равны нулю, каковы величины максимального и минимального определителей, сколько положительных и отрицательных определителей. Эта задача была решена с помощью компьютерного эксперимента. Определителей равных нулю оказалось 2736 (0,75397%). 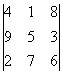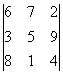Величины максимальных определителей оказались равными 412, а величины минимальных определителей – 412. Таких определителей оказалось по 36. В таблице представлены несколько максимальных определителей.

Таблица. Некоторые максимальные определители.

Положительных и отрицательных определителей оказалось по 180072. Дополнительный визуальный анализ полученных данных показал симметрию полученного распределения относительно максимального значения S = 0. Самое интересное заключается в том, что некоторые величины определителей в распределении отсутствуют, и распределение не носит монотонный характер. Полигон частот определителей по величине S представлен на рис. 1.

Рис. 1. Полигон частот величин определителей.

Нормированная гистограмма частот приведена на рис. 2.

Рис. 2. Нормированная гистограмма частот для величин определителей.

Была проведена статистическая обработка полученных данных для начальных моментов [4]

= , (1)

где N – число определителей, S_i – величина i-го определителя. Для данного распределения были получены следующие числовые характеристики: среднее арифметическое = 0, среднее квадратическое отклонение равно σ = 154,8537, асимметрия A_s = 0 и эксцесс Е_k = 0,274856.

Проблема отыскания определителей с максимальными и минимальными значениями может быть решена другим способом. Можно считать величину определителя S как функцию от 9 независимых переменных a_ij. Найдя частные производные от функции S по этим переменным, и приравняв их нулю, получим 9 алгебраических уравнений. Решение этой системы уравнений приводит к системе 3-х уравнений, зависящих от 6 независимых переменных. Анализ этих производных позволил установить новую закономерность, связывающую частную производную от определителя по независимой переменной a_ij (элементу определителя) с алгебраическим дополнением

= A_ij, (2)

Эта закономерность справедлива для определителей любых порядков. Доказательство этой закономерности основывается на разложении определителя по i строке или j столбцу. Данный элемент входит в разложение только один раз и умножается на алгебраическое дополнение, которое не зависит от этого элемента.

Анализ максимальных определителей, приведенных в таблице, позволил установить еще одну закономерность. Если определитель повернуть на 90⁰ в положительном или отрицательном направлении, то знак определителя изменится на противоположный

↓. (3)

Если такой определитель повернуть еще на 90⁰, то знак определителя изменится на противоположный, т.е. станет таким, какой был у исходного определителя. Величина такого определителя будет равна величине исходного определителя. Это свойство справедливо для определителей любых порядков с любыми элементами. Доказательство не представляет трудностей и начинается с определителей второго порядка.

Для определителей третьего порядка и выше получено свойство, связанное с вычислением величины определителя, полученного в результате перестановки двух элементов определителя (a_ij ↔ a_ik или a_ij ↔ a_kj), находящихся в одной строке или в одном столбце. Величина нового определителя S_n может быть выражена через величины этих элементов и их алгебраические дополнения в исходном определителе

S_n = S – (a_ij – a_ik)∙(A_ij – A_ik), (4)

где S – величина исходного определителя, A_ij, A_ik – соответствующие алгебраические дополнения для элементов a_ij, a_ik.

Для величины нового определителя S_n , полученного заменой двух элементов, находящихся не в одной строке или столбце, получена обобщающая формула

S_n = S – (a_ij – a_lk)∙(A_ij – A_lk) – (–1)^i+j+l+k (a_ij – a_lk)²∙ M_ij,lk , (5)

где M_ij,lk – минор второго порядка/типа. В случае определителя третьего порядка он равен элементу a_vr, где индексы v и r не совпадают с индексами переставляемых элементов. Можно ввести понятие алгебраического дополнения второго порядка

A_{ij,lk =} (–1)^i+j+l+k M_{ij,lk . (6)}

Компьютерный эксперимент, выполненный для получения распределения определителей третьего порядка, позволил получить новую уникальную информацию и закономерности, которые невозможно получить в традиционном подходе. Установлены новые закономерности, связанные с распределением определителей по величине и перестановкой элементов в определителе. Полученные результаты можно использовать в криптографии.

Литература

1. Александрова, Н.В. Математические термины. – М.: Высшая школа,1978. – 190 с.

2. Ефимов, Н.В., Розендорн, Э.Р. Линейная алгебра и многомерная геометрия. – М.: Наука, 1970. – 528 с.

3. Блох, Э.Л., Лопшинский, Л.И., Турин, В.Я. Основы линейной алгебры и некоторые ее приложения. – М.: Высшая школа,1971. – 256 с.

4. Гмурман, В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа,1977. – 480 с.