С.К. Лисин к.т.н., А. И. Федотов д.т.н.

СПб национальный минерально-сырьевой университет «Горный», СПб государственный политехнический университет, Россия

МАТЕМАТИЧЕСКИЕ МОДЕЛИ ВИБРАЦИОННЫХ РЕЖИМОВ

КОНТРОЛЯ ЛИНЕЙНЫХ ПАРАМЕТРОВ

Создание научных основ методов измерений и контроля связано с необходимостью построения теоретических моделей, обеспечивающих повышение точности и эффективности средств измерительной техники. Становятся актуальными исследования прогнозирования динамических режимов, способствующих повышению точности или не обеспечивающих контроль требуемых параметров с помощью измерительных подвижных систем.

Использование электромеханических измерительных систем, подвергнутых динамическому анализу их режимов [1,2], позволяет расширить области применения и повысить эффективность использования вибрационных, виброконтактных и других средств измерений. Элементы и отдельные передачи подобных подвижных систем применяются в устройствах промышленных роботов, в релейных системах обрабатывающих центров, в специальных преобразователях, оснащаемых АЦП и ЦАП устройствами. В практике измерения линейных размеров и перемещений применение электромеханических преобразователей становится особенно необходимым [3,4].

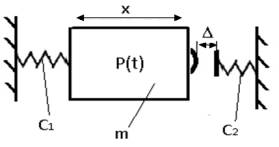
Рассмотрим математические модели колебательных процессов подобных подвижных систем в режиме вибрационного контакта измерительного наконечника с объектом контроля. Расчетная схема одномерного преобразователя (рис. 1) содержит измерительный наконечник, схематизированный в виде поступательно движущейся подпружиненной массы, соударяющейся с поверхностью контролируемого объекта.

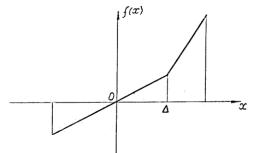
Рис.1. Схема одномерного преобразователя	Рис.2. Схема кусочно-линейной характеристики

Восстанавливающая характеристика f(x) подобной системы, в соответствии с методом кусочно-линейной аппроксимации, в первом приближении представлена упругой компонентой в виде кусочно-линейной двухзвенной несимметричной характеристики (рис.2). На приведенной схеме (рис. 1) приняты обозначения: – координата, отсчитываемая от положения статического равновесия; – масса измерительного стержня; ,– жесткости упругого подвеса и измеряемого объекта; – зазор между измеряемой поверхностью и равновесным положением измерительного стержня.

Исследуем математическую модель несимметричной системы (рис. 1) в режиме вибрационного контакта измерительного наконечника с объектом контроля, находящейся под действием гармонической возмущающей силы известной частоты

, (1)

где – амплитуда возмущающей силы.

Начальную фазу гармонического воздействия полагаем нулевой. При этом нелинейная система упругих характеристик в безразмерной форме имеет вид:

.

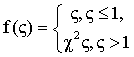В общем виде областью определения функции является интервал [, 1]. Здесь – координата положения измерительного наконечника (), отсчитываемая от равновесного положения; . Областью определения функции является интервал [1, ].

Характеристика в интервалах выражается двумя различными функциями и не является линейной функцией. Такие функции, составленные из отрезков и остающиеся однозначными в закрытом интервале, получили название кусочно-линейных, а в смысле непрерывности – непрерывных по переменной , так как не имеют точек разрыва первого рода.

Как правило, значения принадлежат малой области отклонений от положения равновесия, которая предопределила область малых колебаний твердых тел. С учетом изложенного, движение одномерного преобразователя представляется кусочно-линейной системой дифференциальных уравнений. Дифференциальное уравнение вынужденных колебаний на интервале записывается в виде

, (2)

где

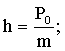
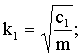
Аналогично, используя принятые обозначения, на интервале имеем

. (3)

Режиму вынужденных колебаний на фазовой плоскости соответствует замкнутая фазовая траектория. Время пробега изображающей точкой всей фазовой траектории совпадает с периодом возмущающей силы. Периоду возмущающей силы соответствует фаза контакта измерительного наконечника, описываемая уравнением (3), и фаза свободного движения измерительного наконечника, описываемая уравнением (2).

Для нахождения точных периодических решений системы уравнений (2), (3) воспользуемся методом «припасовывания». Решения уравнений (2),(3) относительно , содержат произвольные постоянные интегрирования , , А₃ , А₄.

Следуя методу припасовывания, для уравнения (3) принимаем начальные условия:

, (4)

где – момент времени, соответствующий вхождению измерительного наконечника в контакт с поверхностью объекта измерения. Конечные условия для уравнения (3):

(5)

где – момент выхода измерительного наконечника из фазы контакта.

Начальными условиями для уравнения (2), описывающего движение в фазе без контакта, будут условия (5). Следовательно, конечными условиями и одновременно условиями периодичности для уравнения (2) являются условия

, . (6)

Неизвестными в периодических решениях являются постоянные интегрирования и параметры , , , , определяемые из решений системы из восьми уравнений, соответствующих (4-6).

Максимальное отклонение измерительного наконечника от положения статического равновесия вправо определяется из уравнения (3) и условий

, , . (7)

Максимальное отклонение измерительного наконечника от положения статического равновесия влево определяется из уравнения (2) и условий

, , . (8)

С помощью периодических решений, соответствующих (3.34), (3.35) можно вычислить неизвестные . Зная максимальные отклонения измерительного наконечника вправо и влево , можно определить амплитуду и смещение центра колебаний перечисленных решений.

На основе использования условий (4-8) реализуется динамическая задача системы, связанная с построением методом припасовывания («сшивания») решений нелинейных периодических режимов. Процедуры, связанные с установлением функциональной зависимости между измеряемой величиной и параметрами движения системы представляется замкнутой аналитической системой определения неизвестных А, А, А, А, , , , . Для определения неизвестных используется система (7-8).

Рассматриваемые соотношения обеспечивают возможность с одной стороны синтезировать параметры измерительной системы, а с другой – определить погрешность воспроизведения амплитудно-частотной характеристики системы в режиме вибрационного контакта измерительного наконечника [4].

Полученные точные периодические решения недемпфированной системы, соответствуют гармонической внешней нагрузке. Система решений позволяет построить резонансную зависимость . Рассматриваемая расчетная модель строится с учетом упругих свойств измеряемого объекта и применяется для конечных значений параметра .

Литература:

1. Закржевский М.В. Колебания существенно-нелинейных систем.- Рига: Зинатне, 1980. - 190 с.

2. Коловский М.З. Нелинейная теория виброзащитных систем. - М.: Наука, 1966. - 318 с.

3. Федотов, А.И. Теория измерений / А.И. Федотов, С.К. Лисин, Г.С. Морокина. – СПб.: Изд-во Политехн. ун-та, 2013. – 324 с.

4. Лисин, С.К. Технические измерения /С.К. Лисин, А.И. Федотов. – СПб.: Изд-во НМСУ «Горный», 2012. – 66 с.