Иванов В.А., к.т.н., Большев К.Н., к.т.н.,
Степанов А. А., Андреев А.С.
ФГБУН Институт физико-технических проблем Севера
им. В.П. Ларионова СО РАН, г.Якутск, Российская Федерация.
Экспериментальное определение скорости распространения и
ветвления трещины при динамическом разрушении материалов в условиях низких
температур.
Одной из важнейших задач динамической механики
разрушения является изучение динамического распространения трещины в твердых
телах. К наименее изученным проблемам относится измерение скорости ветвления
трещины, которое наблюдается в таких кристаллических и аморфных материалах, как
стекло, сталь, алюминий, полимеры. Кроме того, для суровых климатических
условий Республики Саха (Якутия) особенную важность имеют исследования процессов
разрушения при низких температурах.
Разрушение металлических конструкций в условиях
низких температур имеет весьма негативные последствия. Наблюдаются более высокие скорости
распространения трещины и ее микро и макроветвление, вследствие этого площадь
дефекта значительно увеличивается.
Последствия таких аварийных ситуаций (разрывы трубопроводов и емкостей,
утечки газа, нефтепродуктов, воды, загрязнение окружающей среды) и их
устранение весьма трудозатратно и дорого.
Для успешной реализации исследований в данной
области нами была разработана недорогая, легковоспроизводимая и надежная
методика экспериментального определения скорости трещины при разрушении
стальных конструкций и емкостей в условиях низких температур.
Методика определения скорости
трещины разрабатывалась на основе метода разрыва трещиной проводников. Суть ее
состоит в регистрации времени разрыва токопроводящих линии трещиной, начинающей
движение от инициирующего дефекта при разрывающей образец нагрузке (Рис. 1).
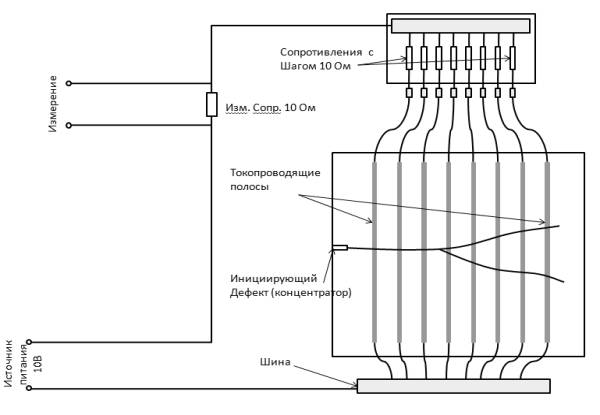
Рис.1. Схема методики определения скорости
трещины
Последовательно с каждой
токопроводящей регистрирующей полосой установлены резисторы. При прохождении
трещины через очередную токопроводящую линию происходит ее разрыв и рост
сопротивления всей батареи, одновременно с этим происходит ступенчатое падение
напряжения на измеряемом сопротивлении. Таким образом, фиксируется время
прохождения трещиной очередной регистрирующей полосы. Величины сопротивлений
резисторов в батарее подобраны таким образом, чтобы каждое последующее было
больше предыдущего на одну и ту же величину, в нашем случае мы выбрали шаг в 10
Ом. (R1=10 Ом, R2=20 Ом, …. RN=N*10 Ом). При выполнении этого условия падение
напряжения на измеряемом сопротивлении при разрыве очередной линии будет
равномерным (рис. 2).
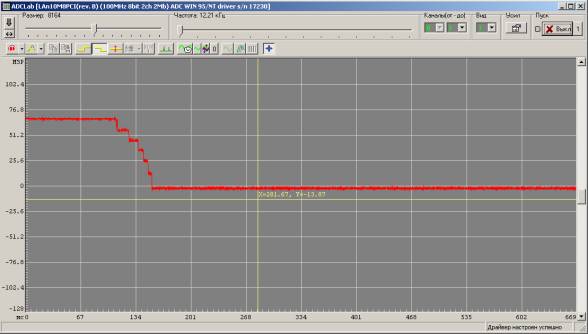
Рис. 2. Интерфейс программного обеспечения
быстродействующей платы АЦП ЛА-н10М8-100 и пример зарегистрированного сигнала.
Для регистрации напряжения на
измеряемом сопротивлении использовалась быстродействующая плата АЦП
ЛА-н10М8-100 производства ЗАО «Руднев-Шиляев». Данное оборудование поставляется
с программным обеспечением, позволяющим
улавливать и записывать изменения сигнала на входе с частотой до 100 МГц (рис.
2).
В качестве модельного
материала при разработке методики использовались пластины из полиметилметакрилата
(ПММА) размерами 150 х 75 мм и толщиной 4 мм (рис. 3). С одного края пластины
наносится искусственный дефект в виде острого клинообразного надреза. Далее
наносятся токопроводящие регистрирующие линии, подсоединяются контакты схемы и
образец устанавливается в зажимы разрывной машины. Разрушение производилось при
монотонно увеличивающейся нагрузке.

Рис. 3. Разрушенный образец из ПММА с
регистрирующими линиями из токопроводящего клея.
В процессе работы было
использовано несколько вариантов выполнения токопроводящих линий:
·
Полосы из
алюминиевой фольги толщиной 0,01мм
·
Полосы из
медной фольги толщиной 0,04мм
·
Медная
проволока диаметром 0,15мм
·
Дорожки из
токопроводящего клея «Контактол»
Алюминиевая фольга имеет
наименьшую толщину из всех вариантов, легко клеится на поверхность образца, но
пайка алюминия возможно только при применении специальных средств и при высокой
температуре, что затруднительно, учитывая малую толщину фольги. Поэтому, для
выполнения соединений с шинами и проводами применялся токопроводящий клей.
Медная фольга и медная проволока легко паяется, но трудно клеится. При этом
медь как материал более пластичный, чем ПММА, при разрушении растягивается и
рвется с задержкой. Наиболее удобным и надежным вариантом в нашем случае
оказались линии из токопроводящего клея (рис. 3). В застывшем состоянии
токопроводящий клей отличается малой пластичностью и толщиной слоя. К
недостаткам такой технологии можно отнести ограниченную доступность такого
клея, а также относительно высокое удельное сопротивление (сопротивление полосы
длиной 6-7 см и шириной 3 мм примерно 3 Ом).
Для охлаждения образца при
проведении экспериментов при отрицательных температурах приближенных к
климатическим зимним условиям Якутии, мы использовали жидкий азот (температура
-196°С). Для этого установленный в зажимы образец теплоизолировался
и постепенно доводился до необходимой температуры тонкой струей азота. Для регистрации температуры на
образце использовалась термопара ТХА и преобразователь сигналов «Теркон».
После отработки методики была
проведена серия экспериментов на разрушение образов из ПММА при комнатных
температурах (~20°С) и при низких температурах (~ -40°С - -60°С). В результате
получены данные, хорошо согласующиеся с литературными данными и с данными
теоретических расчетов. На рис. 4 Представлен вид разрушенного при -35 С
образца и полученный при этом сигнал. При этом каждое ступенчатое изменение
сигнала соответствует прохождению трещиной очередной регистрирующей полосы.
На рисунке также видно
множественное ветвление трещины, так что определенная таким образом величина
соответствует скорости основной макротрещины распространяющейся быстрее
остальных.

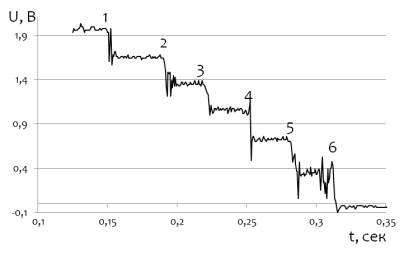
Рис. 4. Разрушенный при
-35 С образец и полученный при этом сигнал.
Таблица 1. Вычисленные
средние скорости трещины на участках.
|
Участок |
Длина, мм |
Время, мсек |
Скорость, м/сек |
|
12 |
14,8 |
0,03968 |
745,9677 |
|
23 |
13,9 |
0,03008 |
924,2021 |
|
34 |
13,1 |
0,03008 |
871,0106 |
|
45 |
11,5 |
0,03136 |
733,4184 |
|
56 |
12,9 |
0,02624 |
983,2317 |
Методика, представленная в
статье планируется к применению для определения скорости трещины при разрушении
стальных трубопроводов и сосудов высокого давления в условиях низких
температур.
Основным плюсом разработанной методики является
возможность проведения экспериментов в опасных и экстремальных условиях,
например при разрушении сосудов высоким внутренним давлением, или при
экстремально низких температурах. Использование традиционного метода
высокоскоростной съемки в данных условиях весьма затруднено. Также к
достоинствам методики можно отнести доступность, дешевизну и простоту.
К недостаткам можно отнести
шумы при размыкании трещиной токопроводящих линий. Данное явление, вероятно,
возникает из-за несовершенства блока питания схемы. Также затрудняет проведение
экспериментов работы по подготовке образца. Так, например, в случае испытаний
стальных сосудов необходимо проводить очистку поверхности, нанесение слоя
диэлектрика (изолирующей краски) наклейку контактных площадок и регистрирующих
полос и повторную гидро- и токоизоляцию.
Литература:
1. Алексеев A. А., Сыромятникова А. С., Большев К. Н. Разрушение твердых тел при быстром распространении и ветвлении трещин. / Монография. //LambertAcademicPublishing.Саарбрюккен.-2013.
2. Серенсен С.В. Прочность пластмасс / Я. Немец, С.В. Серенсен, В.С. Стреляев. – М.: Машиностроение, 1970. – 335 с.
3.
Ravi-ChandarK.
An experimental investigation into dynamic fracture. III. On steady-state crack
propagation and crack branching /K. Ravi-Chandar, W.G. Knauss // International
Journal of Fracture.- 1984.- №26.- Р.141-154.
4.
Sharon
E. Microbranching instability instability and the dynamic fracture of brittle
materials / E. Sharon, J.Fineberg // Physical Review B. – 1996. – V.54, №10. –
P.7128-7139.
5. Бедий И.Н. Кинетика быстрых трещин и ветвление: Автореф. Дис. канд. техн. наук:01.02.06. / И.Н. Бедий; ИПП АН УССР. – Киев, 1990. – 17 с.
6. Динамическая стохастичность и скейлинг при распространении трещины / О.Б. Найнмарк, В.А. Баранников, М.М. Давыдова и др. // Письма в ЖТФ. – 2000. – Т.26, Вып. 6. – С.67-77.
7. Экспериментальное и теоретическое исследование динамической стохастичности и скейлинга при распространении трещины / О.Б. Найнмарк, М.М. Давыдова, О.А. Плехов, С.В. Уваров // Физическая мезомеханика. – 1999. – Т.2, №3.-С. 47-58.
8. Уваров С.В. Экспериментальное исследование эффектов нелинейной динамики распространения трещин: Дис. … канд. физ-мат. наук: 01.02.04 / С.В. Уваров; ИМСС УрО РАН. – Пермь, 2000. – 131 с.
9. Плехов О.А. Моделирование нелинейной динамики трещин и локализованного разрушения в волнах нагрузки: Автореф. дис. … канд. физ. – мат. наук: 01.02.04 / О.А. Плехов; ИМСС УрО РАН. – Пермь, 2000. – 17 с.