Строительство и архитектура/4. Современные строительные материалы

Севастьянов Р.В., Курбатов Ю.Е.

Пермский национальный исследовательский
политехнический университет, Россия

Математическое моделирование усталостной прочности многокомпонентных композитов на органоминеральном вяжущем при циклическом нагружении

Одной из наиболее актуальных и важных задач в строительстве является задача оценки долговечности или длительной прочности строительных конструкций и сооружений, как в рамках задачи о прогнозировании ресурса строительной конструкции, так и в задаче моделирования прогрессирующего разрушения, где также требуется использование кинетических уравнений. При этом одной из составляющих данной задачи является проблема прогнозирования усталостных свойств строительных материалов, находящихся под воздействием циклических нагрузок. Традиционно одним из наиболее применяемых материалов в строительстве является бетон, который можно рассматривать как классический композит, механические свойства которого определяются с позиции аппарата механики композитов. Механика разрушения композиционных материалов представляет собой сложный процесс, обусловленный как рассмотрением компонентов композита на разных масштабных уровнях, так и различными свойствами самих компонентов, входящих в состав композита. В частности, поведение композиционных материалов под воздействием циклического нагружения зависит от многих факторов, в том числе от состава и структуры материала.

Авторами данной статьи была поставлена цель: разработать методику оценки несущей способности бетонных строительных конструкций, находящихся в условиях действия значительных нестационарных нагрузок, путем моделирования структурных механических свойств бетона.

Разрушение бетонного материала происходит в результате необратимого накопления повреждений в цементных компонентах бетона. Зная усталостные характеристики цементного материала, полученные опытным путём, можно присвоить их соответствующим элементам численной модели бетона. Проведение вычислительного эксперимента позволяет получить поверхность длительной прочности композита, формализованную в виде кривой Вёлера для всего бетонного материала в целом и в дальнейшем использовать её при расчетах усталостной долговечности строительных конструкций зданий и сооружений. Для реализации численного эксперимента была принята упрощенная структурная модель бетона, представленная на рисунках 1 и 2.

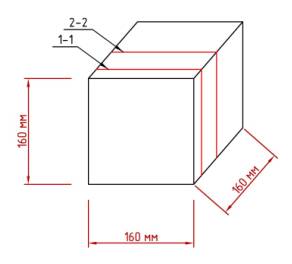
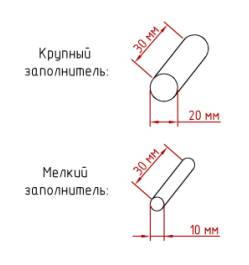
Рис. 1. Структурная модель бетона

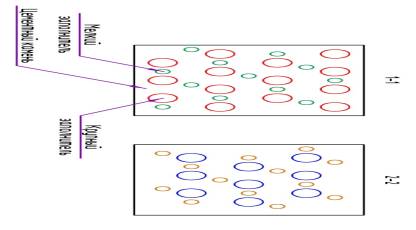
Рис. 2. Компановка заполнителя

Постановка краевой задачи в данном случае является традиционной для структурно-феменологического подхода. Тензоры жесткости, поврежденности и полей напряжения зависят от радиус-вектора (пространственных координат). Тензор поврежденности 4-го ранга является бинарным и принимает значения нулевого или единичного тензора скачкообразно, в зависимости от того, достигла ли скалярная поврежденность значения единицы. Далее приведены основные соотношения теории упругости и механики разрушения, необходимые для постановки краевой задачи:

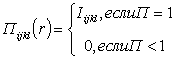
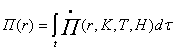
Механизм усталостного разрушения композиционных материалов напрямую зависит от неоднородности их реальной структуры. Для оценки усталостной долговечности бетона при заданных условиях необходимо постоянно отслеживать процесс накопления повреждений в материале. Накопленные экспериментальные данные говорят о сложном характере физических процессов, протекающих при этом в материале. Описание кинетики разрушения сводится к определению величины повреждений, накопленных за произвольный промежуток времени. В обзорной статье [1] описаны основные подходы к определению величины накопленных повреждений, которую в общем случае принято называть поврежденностью материала.

Многократность элементарных актов разрушения является отличительной особенностью усталостной работы материала. Распределение напряжений и деформаций по объему бетона происходит неоднородно, в результате чего процессы накопления повреждений в отдельных точках объема протекают неодинаково. В процессе циклического нагружения происходит разрушение отдельных структурных элементов. В результате каждого такого разрушения происходит перераспределение напряжений и при определении значения поврежденности материала в каждой точке объема необходимо последовательно менять закон накопления повреждений в соответствии с новой картиной НДС. Таким образом, усталостное накопление повреждений следует рассматривать как процесс наследственного типа.

Для проведения численного моделирования усталостной долговечности бетона авторами была разработана модель накопления повреждений, которая основана на гипотезе Болотина об автомодельности данного процесса [2]. С целью упрощения поставленной задачи заполнитель был принят абсолютно неразрушаемым материалом, прочностные характеристики которого на порядок больше цементного компонента. Таким образом, задача определения усталостной долговечности бетона свелась к определению количества циклов, приложенных до момента полного разрушения цементной составляющей бетона.

Поврежденность цементного материала можно представить как функцию, зависящую от критерия нагружения К и текущего времени нагружения Т. При этом функция П = f (К,Т) в рамках разработанной модели изображается в виде поверхности, которая может быть построена на основании реперных кривых, полученных в результате натурных испытаний цементных образцов (см. рисунок 3). Сечение поверхности повреждения плоскостью П = 1 по сути своей является усталостной характеристикой цементного материала, т.е. кривой Вёлера.

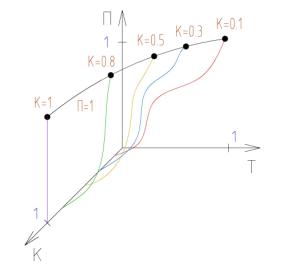
Рис. 3. Поверхность поврежденности, состоящая из реперных кривых

Описанная выше модель накопления повреждений использовалась для вычисления на каждом этапе нагружения текущих поврежденностей цементных элементов бетона, единичные значения которых могут служить индикатором разрушения. Пошаговое моделирование процесса накопления повреждений на ЭВМ с учетом постоянного перераспределения напряжений и уже накопленной поврежденности элементов дает возможность учитывать влияние истории нагружения на усталостную характеристику бетона.

Зерна заполнителя, имеющие форму цилиндров, и цементный камень моделировались путем послойного выдавливания соответствующих плоских фигур. Вид геометрической модели бетона, созданной в ANSYS, приведен на рисунке 4.

Рис. 4. Расчетная модель бетона

Для каждого типа материала (в данном случае их 2 – заполнитель и цементный камень) были определены свои физические свойства, необходимые для решения данной задачи. Свойства назначались соответствующим объемам еще до разбиения на конечные элементы. В рамках данной задачи для описания свойств материалов были использованы 2 показателя – модуль упругости и коэффициент Пуассона.

Таблица 1

Физические свойства элементов структуры

Материал	Модуль упругости Е,	Коэф-нт Пуассона
Щебень	47	0.25
Цементный камень	25.3	0.28

Для реализации построенной модели бетона был выбран конечный элемент SOLID 65, предназначенный для моделирования объемных тел. Общее количество конечных элементов после разбиения составило 52682 штук, из них 42188 элементов являлись компонентами цементного камня.

В соответствии с поставленной задачей для построения полноценной кривой Вёлера бетонного материала вычислительный эксперимент необходимо воспроизвести несколько раз при различных значениях нагрузки. Вышеупомянутые значения (уровни) нагружения приведены в таблице 2.

Таблица 2

Уровни нагружения

Уровень	№ 1 (0,1)	№ 2 (0,5)	№ 3 (0,9)
Значение, Па	4 903 350	24 516 750	44 130 150

Нагрузка прикладывалась растягивающая, распределенная по одной из плоскостей модели. При этом противоположная сторона модели была закреплена от всех возможных перемещений и поворотов.

Для имитации разрушения элементов в процессе выполнения программы расчета применялась опция “Рождение и смерть элемента”, позволяющая активировать или деактивировать отобранные конечные элементы при моделировании процесса разрушения. Алгоритм проведения расчета в ПК ANSYS был реализован на параметрическом языке программирования APDL в соответствии с указаниями учебного пособия [3].

В ходе выполнения вычислительного эксперимента было проведено три серии расчетов численной модели бетонного композита. Каждая серия характеризовалась своим значением (уровнем) прикладываемой к модели нагрузки. Значения усталостной долговечности бетонного материала, полученные в результате проведения вычислительного эксперимента, приведены в таблице 3.

Таблица 3

Значения усталостной долговечности расчетной модели

Нагрузка		Количество циклов до разрушения N
Нормированные значения (безразмерные)	Натуральные значения (Па)	Нормированные значения (безразмерные)	Натуральные значения (кол-во циклов)
0,1	4 903 350	5,92446	29 622 300
0,5	24 516 750	1,40829	7 041 450
0,9	44 130 150	0,02296	114 800

На основании полученных данных можно построить кривую Вёлера, которая будет являться усталостной характеристикой бетонного материала и может применяться при расчетах зданий и сооружений на усталостное разрушение. Данная кривая приведена на рисунке 5.

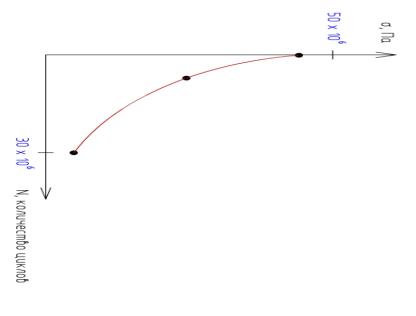
Рис. 5. Кривая Вёлера для бетонного материала

При разработке гипотезы накопления повреждений было выдвинуто теоретическое предположение о том, что разрушение модели бетона произойдет, когда разрушатся все цементные элементы. На практике при выполнении вычислительного эксперимента авторами было выявлено, что модель теряет свою целостность, прочностные и жесткостные характеристики задолго до разрушения всего цементного камня. Так, на определенном этапе моделирования система выдавала сообщение о том, что происходит движение элементов твердого тела в результате нарушения сплошности модели.

В таблице 4 приведены рисунки, иллюстрирующие кинетику накопления необратимых повреждений, снятую для одной из наружных плоскостей модели в различные моменты нагружения.

Таблица 4

Кинетика накопления повреждений на одной из поверхностей “куба”

Количество пройденных циклов	0	3 520 725	7 041 450
Поля напряжений

На основании методики, разработанной в данной работе и подтвержденной серией вычислительных экспериментов, можно сформулировать алгоритм экспериментально-теоретического исследования какой-либо конструкции, здания или сооружения на усталостное разрушение.

1) Проведение полнофакторного натурного эксперимента с целью получения кривых поврежденности цементных образцов;

2) Построение структурно-феноменологической модели, которая соответствует конкретному классу, марке и прочим характеристикам рассчитываемого бетона;

3) Проведение серии вычислительных экспериментов с целью получения кривой поврежденности для исследуемого бетонного материала;

4) Построение численной модели рассчитываемой конструкции, здания или сооружения;

5) Проведение вычислительного эксперимента с использованием полученной кривой поврежденности и формулирование выводов об усталостной долговечности конструкции.

В результате выполнения указанного расчета можно получить текущие значения накопленной поврежденности в определенных точках конструкции, здания или сооружения. Данная информация позволяет судить о механической безопасности зданий и сооружений на определенном этапе их эксплуатации. Кроме того, разработанная методика может применяться в научных целях для исследования усталостной природы накопления повреждений в композиционных материалах и прогнозирования их разрушения.

Литература:

1. Севастьянов Р.В. Модели накопления повреждений строительных материалов при нестационарном термомеханическом воздействии / Р.В. Севастьянов, Ю.Е. Курбатов // Вестник ПНИПУ. Урбанистика. – 2013. - №3(11). – С. 44 – 53

2. Болотин, В.В. Прогнозирование ресурса машин и конструкций / В.В. Болотин. – М., 1984. – 312 с.

3. Котов А.Г. САПР изделий из композиционных материалов. Моделирование процессов деформирования и разрушения в среде ANSYS / А.Г.Котов. – Пермь: Изд-во Перм. гос. техн. ун-та, 2008. – 351 с.