УДК
622.775
Канд.техн.наук
Сабирова Л.Б.
Казахский Национальный технический университет
имени К.И.Сатпаева
ФИЗИЧЕСКИЕ МОДЕЛИ
ДИФФУЗИОННОГО РАСТВОРЕНИЯ МЕТАЛЛОВ ДЛЯ УСЛОЖНЕННЫХ УСЛОВИЙ ЗАЛЕГАНИЯ ПЛАСТОВ
Прежде чем переходить
к обсуждению и моделированию фильтрации растворов в пористой среде
продуктивного пласта и вмещающих пород кратко остановимся на модели физического
процесса диффузионного растворения металла. Основная расчетная модель этого
процесса, полученная нами ранее, сведена к уравнению:
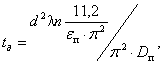 сут, (1)
сут, (1)
где tд – время диффузионного
растворения куска руды диаметром d,
см; eп – проектное значение
коэффициента извлечения металла, доли ед.; Dп – коэффициент эффективной диффузии, см2/сут.
Из
формулы (1) следует, что время растворения металла зависит прежде всего от
размеров d и от Dп.
Понятно,
что первая величина d
относится к разряду неуправляемых параметров при подземном скважинном
выщелачивании металлов.
Вторая
величина Dп в принципе также
относится к неуправляемому параметру.
Физические модели диффузионного растворения и фильтрационного переноса
металлов рассматривались нами ранее для совершенных скважин. Для сложных
условий, оцениваемых критериями такие модели отсутствуют, и их следует
скорректировать.
Рассмотрим диффузионное растворение
металла в реагенте.
В
соответствии с законом диффузии Фика запишем модель в виде дифференциального
уравнения [1]:
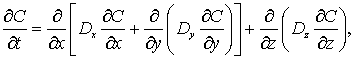
где C(x,
y, z, t)
– искомая функция распределения металла в пространстве по времени t; Dх; Dу; Dz - коэффициенты диффузии
по координатам х, у, z.
Для
наших исследований интерес представляет одномерный (линейный) закон диффузии,
который описывается уравнением:
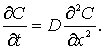 (2)
(2)
Следует
искать решение (2) в виде функции С(x, t)
при следующих граничных условиях:
C(x,
t) = Co
при 0 < x < 1 и t = 0;
C(x,
t) = 0 при x = l, x
= 0, t > 0,
где Со – исходная концентрация
металла, т/см3;
C(x,
t) – текущая концентрация металла по оси х за время t;
l - размер куска руды,
см;
t
– время диффузии, сут.
Имеется
решение такого уравнения [1] в виде бесконечного
ряда:
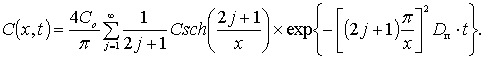 (3)
(3)
Если
положить, что в относительных единицах Со = 1, а Спр
= 0,75, т.е. конечное значение диффундирующего металла (растворения) до 75 %,
то можно получить простейшее решение, ограничившись первым членом быстро
убывающего ряда (3):
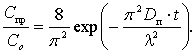 (4)
(4)
При
заданном Dп @ 0,864×10-3 см2/сут.
из (4) находим время диффузионного выщелачивания металла:
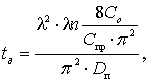 сут, (5)
сут, (5)
где l - средний диаметр куска
руды, см;
Со
= 1 и Спр @ 0,7 ¸ 0,75 – относительные
единицы содержания металла в руде и извлечения его из руды;
Dп – эффективный
коэффициент диффузии, м2/сут, для металлов [1]
Dп @ 0,864×10-3 см2/сут.
Анализ
формулы (2.5) показывает, что она обладает некоторыми недостатками. Первое - Спр
@
0,7 ¸
0,75, т.е. весьма узкий, хотя и практически правильный диапазон изменения
коэффициента извлечения металла. Второе – при увеличении Спр
от 0,7 до 0,75 время tд
будет уменьшаться, что является противоречием.
Исходя из этих замечаний, запишем
формулу (5) в виде:
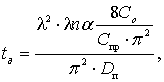 сут, (6)
сут, (6)
где a - некоторый параметр, l > 0, который
определяется статистическим путем или экспериментально по схеме.
Для
определения a принимаем Спр
= 0,7, тогда формулу (6) запишем:
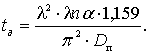 (7)
(7)
Из
уравнения (7) имеем:
![]() (8)
(8)
Из
уравнения (8) легко определить искомый параметр a из уравнения:
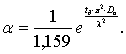 (9)
(9)
Следовательно,
если известно время диффузионного выщелачивания - tд
и размер куска l, то по формуле (9)
легко подсчитать параметр a.
Например,
для руды месторождения Тохтазан имеем: l = 2 см, Dп = 0,864×10-3 см2/сут,
tд = 36 сут.

Следовательно, для условий руды
месторождения Тохтазан имеем уравнение:
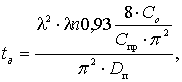 сут. (10)
сут. (10)
Кроме
того, величину a можно рассчитать, если
известна функция извлечения металла e(t) в виде:
![]() (11)
(11)
где С1 – параметр,
определяемый статистически.
Пусть
имеем для условий месторождения Тохтазан e(t) = 0,65; tд = 40 сут.
Из уравнения (11) имеем:
![]() (12)
(12)
откуда, решая (12) относительно С1,
получим:
![]()
или

![]()
При этом, уравнение (11) запишется в виде:
![]() (13)
(13)
Пусть
задано t
= 20 сут, тогда:
e(t) = 0,48, т.е. » 50 % за 20 суток.
Рассмотрим
более сложную руду месторождения Пустынное, для нее tд
= 340 сут; e(t) = 0,3 или 30 %, тогда
имеем:
![]()
Для извлечения металла до e = 0,5 получим формулу:
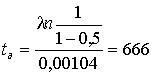 суток,
суток,
т.е. в принципе и
сульфидные руды можно выщелачивать, только срок существенно растягивается.
Определим параметр a для руд месторождения
Пустынное по формуле (9):

Тогда
формула (6) для определения tд
для руд Пустынного будет:
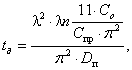 сут. (14)
сут. (14)
Если
теперь отделить фракцию 0,5 см и ниже, то время сократится:
![]() суток,
суток,
а при крупности l = 0,6:
![]() суток.
суток.
Из полученных формул следует сделать выводы.
1.
Выведены новые формулы (5), (6) для вычисления времени диффузионного
растворения металлов от влияющих факторов: среднего размера куска руды - l, коэффициента диффузии
- Dп, коэффициента
извлечения металла – Спр при его выщелачивании.
2.
Наиболее сильно на время диффузионного выщелачивания - tд металла влияет
размер куска руды, которое пропорционально
квадрату линейного размера куска.
Для
проектирования технологических систем выщелачивания металлов одним из главных
параметров является время диффузионного растворения и извлечения конкретного
металла до проектного значения коэффициента извлечения. Диффузионное
растворение металлов достаточно теоретически освещено в известной монографии П.
Шьюмана [1] и других работах [2, 3]. Однако до сих пор нет достаточно надежных
аналитических методов, позволяющих определить время растворения металлов в
функции от основных влияющих факторов.
Будем
следовать П. Шьюмону [1] и искать расчетные модели для определения времени диффузионного
растворения металла для идеальных форм рудного или иного сырья.
Рассмотрим
дифференциальное уравнение (2) второго закона Фика при одномерной диффузии в
пластине:
![]() (15)
(15)
где С(x, t) – концентрация вещества С как функция одной координаты – х и времени t;
Dп – эффективный
коэффициент диффузии.
Если
принять, что Dп не зависит от времени и от координаты х, то известно решение (15) в виде бесконечного сходящегося ряда:
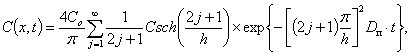 (16)
(16)
где ![]()
Со – начальная концентрация
металла в пластине – h;
х – глубина диффузии.
При
выщелачивании практически невозможно определить концентрацию полезного
компонента – металла на различной глубине куска. Для получения общего количества выщелоченного металла необходимо
знать среднюю концентрацию металла ![]() в идеальной пластине, толщиной – h. Для этого необходимо
взять интеграл от функции (16) по h
в виде:
в идеальной пластине, толщиной – h. Для этого необходимо
взять интеграл от функции (16) по h
в виде:
![]() (17)
(17)
Подставляя
в (17) значение С(x, t) (16) после
интегрирования и необходимых преобразований получим новый ряд:
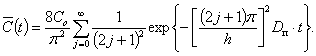 (18)
(18)
Рассмотрим функцию ряда -
![]() до 3-го члена включительно, тогда получим:
до 3-го члена включительно, тогда получим:
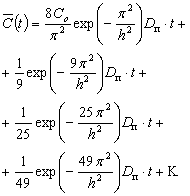 (19)
(19)
С
погрешностью не более 3% можно из (19) записать уравнение:
![]() (20)
(20)
Решая
уравнение (20) относительно времени t выщелачивания до ![]() ,
получим:
,
получим:
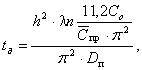 сут, (21)
сут, (21)
где h измеряется в
сантиметрах;
Dп измеряется в см2/сут;
Со и ![]() - измеряются в относительных единицах,
поэтому Со = 1, а
- измеряются в относительных единицах,
поэтому Со = 1, а ![]() равно проектному коэффициенту извлечения
металла из руды, т.е.
равно проектному коэффициенту извлечения
металла из руды, т.е. ![]() = eп.
= eп.
Формула
(21) является основополагающей для определения времени диффузионного
растворения металла при выщелачивании из пластин.
Рассмотрим
численный пример.
Пусть
дано: h = 2 см, Спр = 0,7, Dп = 0,864×10-3 см2/сут.
[1], тогда:
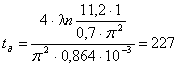 суток.
суток.
Если,
например, крупность кусков породы уменьшить вдвое, т.е. h = 1 см, то время сократится в четыре раза и составит tд = 57 суток, а при h = 0,5 см
всего 14 суток. Из этого простого примера следует, что размер куска
рудного сырья является главным показателем при диффузионном растворении.
Рассмотрим
также решение задачи определения времени диффузионного растворения для шара с радиусом
– r, см. В сферической системе координат второй
закон Фика имеет вид [1]:
![]() (22)
(22)
Известно
решение этого уравнения для малых времен в виде для среднего значения ![]() :
:
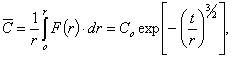 (23)
(23)
где
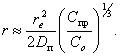 (24)
(24)
Подставляя
(24) в уравнение (23) и решая его относительно времени tд, получим для шара:
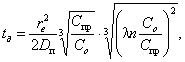 сут.
сут.
или иначе
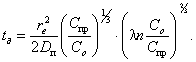 (25)
(25)
Сопоставим
теперь численные значения для пластины (21) и шара для только что
рассмотренного примера.
По
формуле имеем при l = 2 см, тогда r = 1 см:
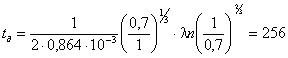 суток.
суток.
При
r = 0,5 см, tд = 64 сут; и при r = 0,2 см, tд = 16 суток.
Из
приведенных данных следует, что формулы (21) и (24) дают практически одинаковый
результат.
Полученные
путем теоретического анализа фундаментальные формулы для вычисления времени
диффузионного растворения или выщелачивания металлов рекомендуются для
практических расчетов при проектировании и управлении технологических систем
подземного скважинного выщелачивания.
ЛИТЕРАТУРА:
1.
Шьюман
П. Диффузия в твердых телах, М., Наука, 1968, 320с.
2.
Рогов
Е.И., Язиков В.Г., Рогов А.Е. Математическое моделирование в горном деле.
Алматы, Lem., 2002, 204с.
3.
Рогов
А.Е., Рыспанов Н.Б. Математические основы геотехнологии. Алматы., FORTRESS,
2007, 367с.