Безвесильная Е.Н. д.т.н., проф., Ткачук А.Г. к.т.н., Коваль А.В. к.т.н.

Национальный технический университет Украины "КПИ", Украина

Житомирский государственный технологический университет, Украина

 

ЦИФРОВОЕ МОДЕЛИРОВАНИЕ УРАВНЕНИЯ ДВИЖЕНИЯ АВИАЦИОННОЙ ГРАВИМЕТРИЧЕСКОЙ СИСТЕМЫ

 

На сегодняшний день информация о гравитационном поле Земли необходима в авиационной и космической технике (коррекция систем инерциальной навигации ракет, самолетов, орбит космических летательных аппаратов), для исследования геодинамических явлений, для реализации целей инженерной геологии, археологии, прогноза землетрясений и т.д. Для определения характеристик гравитационного поля Земли удобнее использовать авиационные гравиметрические системы (АГС). С помощью именно АГС можно получить гравиметрическую информацию в труднодоступных районах земного шара гораздо быстрее и с меньшими затратами, чем с помощью других гравиметрических средств или систем. В целом АГС должна состоять из подсистем, которые выполняют следующие функции: измеряют ускорение силы тяжести (гравиметр), определяют координаты местоположения, скорость, измеряют высоту, осуществляют вычислительные операции. Все подсистемы имеют собственные погрешности, которые непосредственно влияют на конечные выходные показания АГС. Поэтому необходимо определить допустимые значения погрешностей измерения параметров движения самолета (ЛА) компонентами АГС [1-4] и провести соответствующее моделирование.

Актуальность рассматриваемой проблемы состоит в следующем: заданную точность измерения  в (1-3) мГал [1] можно обеспечить только в том случае, если отдельные сборочные приборные компоненты АГС определяют основные показатели (скорость, курс, ускорение и др.) с требуемой точностью. В известной литературе такие решения заданной проблемы отсутствуют. Поэтому задача определения методических погрешностей и цифровое моделирование сборочной авиационной гравиметрической системы c целью изучения вли­яния различных параметров (курса, широты, скорости, высоты полета самолета) на результаты измерений  является актуальной.

В работах[1, 3] получено уравнение для определения аномалии ускорения силы тяжести с помощью АГС:

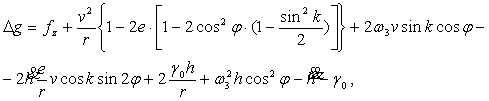             (1)

где  - путевая скорость самолета; -выходной сигнал гравиметра; r - радиус местоположения ЛА; ,  - вертикальные скорость, ускорение ЛА;  - угловая скорость вращения Земли; е - сжатие Земли; , ,  - широта, курс, высота местоположения ЛА; - справочное значение ускорения силы тяжести.

Используем уравнение (1) для вычисления допустимых погрешностей измерения параметров движения ЛА компонентами АГС. Перепишем его в виде [1]:

                                                        (2)

где D – суммарная погрешность АГС:

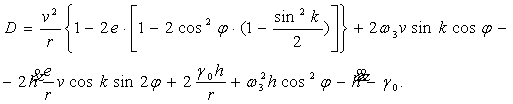           (3)

Параметры, входящие в равенство (3), определяются отдельными подсистемами АГС.

При моделировании и при экспериментальных исследованиях так же, как и при теоретических исследованиях, применялась разработанная уточненная математическая модель (1) АГС. В практике гравиметрических измерений в известной литературе подобная проблема не ставилась и не освещалась.

Было проведено моделирование-исследование с помощью ЭВМ, направлен­ное на решение следующей научно-технической проблемы - изучение вли­яния различных параметров (курса, широты, скорости, высоты полета самолета) на результаты измерений с целью определения некото­рых закономерностей и выработки рекомендаций по методике проведе­ния авиационных гравиметрических измерений. Разработаны программы, алгоритмы, получены результаты исследования - таблицы рассчитанных значений  , по экспериментальным данным для различных маршрутов полета самолета: при различных курсах (полеты вдоль меридианов); при различных широтах (полеты вдоль параллелей); при различных значениях высоты самолета; при различных значениях скорости самолета.

В соответствии с программой исследований , были получены рис. 1-2.

 

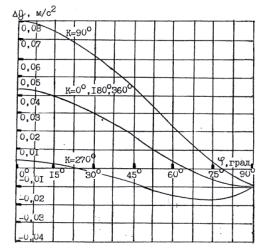
а)                                                       б)

Рис. 1. Зависимость  (для = 5000 м, =40 м/с, =258 м/с) от: а) широты местоположения объекта при полетах ЛА вдоль меридианов; б) курса местоположения объекта при полете ЛА вдоль параллелей

 

Анализ графиков на рис.1-2 позволяет сделать следующие вы­воды: показано, что если при проведении авиационных гравиметрических измерений вдоль земного меридиана () необходимо точно из­мерять курс, то при движении вдоль земной параллели () важно точное определение скорости.

        

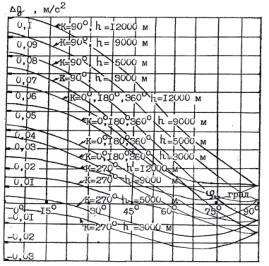
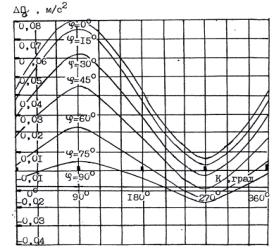
а)                                                                   б)

Рис. 2. Зависимость аномалий ускорения силы тяжести (для = 5000 м, =40 м/с) от: а) высоты полета ЛА; б) скорости полета ЛА

 

Моделированием и эксперименталь­но подтверждено, что чувствительность АГС к ошибкам измерения скоро­сти будет максимальной для восточного и западного курсов при широ­те  , минимальной при движении самолета с северным и южным курсом и при независимо от курса. Моделированием и экспериментально подтверждено, что чувствительность ошибки выходного сигна­ла АГС к ошибкам измерения широты будет максимальна при движении самолета на восток и минимальна при движении самолета на запад. Чувствительность ошибки выходного сигнала системы к ошибкам измерения широты будет максимальна при движении самолета в средних широтах  и близка к нулю для всех курсов при работе АГС на экваторе, а для самолета, движущегося с курсом  или  , - при .

Моделированием и экспериментально подтверждено, что при движе­нии самолета с северным или южным курсом чувствительность ошибки выходного сигнала АГС к ошибкам измерения курса будет наибольшая; при движении самолета с восточным или западным курсом чувствитель­ность ошибки выходного сигнала АГС к ошибкам измерения курса будет наименьшая.

 

Выводы

Проведено цифровое моделирование уравнения движения (1) сборочной АГС с целью изучения вли­яния различных параметров (курса, широты, скорости, высоты полета самолета) на результаты измерений .

Установлено, что чувствительность АГС к ошибкам измерения скоро­сти будет максимальной для восточного и западного курсов при широ­те  , а минимальной при движении самолета с северным и южным курсом и при независимо от курса; к ошибкам измерения широты будет максимальна при полете самолета на восток и минимальна при полете самолета на запад; к ошибкам измерения курса будет наибольшая при полете самолета с северным или южным курсом, а наименьшая при полете самолета с восточным или западным курсом.

 

Литература:

1.       Безвесільна О.М. Авіаційні гравіметричні системи та гравіметри: монографія. Житомир: ЖДТУ, 2007, 604 с.

2.       Bezvesilnaya E.N., Tkachuk А.G., Kozko K.S. System for airborne gravimetry // European Applied Sciences (Germany). 2013. № 5(2). P. 37–39.

3.       Безвесільна О.М. ,Ткачук А.Г. Науково-теоретичні дослідження нового п’єзоелектричного гравіметра автоматизованої авіаційної гравіметричної системи в екстремальних умовах з використанням нейронних мереж: монографія. Житомир : ЖДТУ, 2014, 225 с.

4.       Безвесільна О.М. Дослідження нової прецизійної інерціальної навігаційної системи при авіаційних гравіметричних вимірюваннях: монографія. Житомир: ЖДТУ, 2012, 476 с.