Kraeva E.M.
Siberian State Aerospace University named after M.F.
Reshetnev, Russia
A model for calculation channels of a centrifugal
hydraulic machine
In the centrifugal hydraulic machines, there is unevenness in flow and
vortex interaction along the radius main fluid flow and in the lateral axil of
the pump [1]. Blades convey energy to fluid flow, a portion of which moves in the
lateral axil with a lag from the main. In the result, flow is formed, the same
as in the channel behind the poorly streamlined body. This flow is
characterized by the appearance of return currents and vortices [2]. This
process is determined by the ratio of width to channel length, the thickness of
the boundary layer on the walls and the relative height of the blade.
Interaction of flows in the axil and in the channels leads to the circulation
of the vortex flow in the area behind the ledge.
On the basis of flow visualization researches, the
results of [2] and measuring its parameters in the gap between the rotating
impeller blades with open ends and sleek body, a calculation model can be
represented for the jet-vortex flow around impeller channels. The flow of fluid
in an inter-blade channel of such impeller is exposed to direct force influence
of the blades. Fluid in the axial gap 
is twisted by the
forces of friction and slipping relative to the ends of the blades of the
impeller. Consequently, on one and the same radius, the particle of the liquid
in the channel and in an axial gap 
are moving with
different circumferential speed, which leads to their relative movement in the
radial and axial directions.
The pattern of the flow in
the channels is defining influenced mainly by the parameters of the mixing zone
and the vortex flow. Based on the analysis of the flow pattern in the flow in
rectangular cavities presented in photographs at the work [3], it should be
noted that for the flow around a square channel for ratio 
there is unique stable vortex, spinning almost like a solid body.
With a further increase in the depth of the channel to 
we observe two vortex cells arranged one over another and having
the opposite direction of rotation. Minimization
of hydraulic losses in the channels of the impeller prevents multivortex flow
both in depth and width of the channel for the region in which the energy return singlevortex current reaches a maximum, we
obtain
. (1)
The minimum possible value of the impeller channel on the
basis of (1) is
. (2)
We find the minimum width of the blade at the outlet of
the impeller on the condition of preserve the flow core in the inter-blade
channel that will simultaneously the condition of applicability of the theory
to the calculation of impeller channels.
The critical value of the parameter
.
At the same time the area of the flow core coincides with
the end of the first portion and the width of the blade at which the core is
retained and does not flow beyond the first portion of the circulation zone under
[2], will be
(3)
According to
the calculated length of the channel under certain width and diameter of the
impeller the optimum number of blades
is
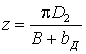. (4)
The high
degree of non-uniformity of the flow of liquid at the outlet from the
centrifugal impeller and its vortex structure in the side cavity in the high
speed pumping unit leads to a substantial loss of energy.
Experimental
data generally confirm the accepted model for calculating the half-open
channels of the impeller in the form of jet-vortex flow in a three-zone field
of centrifugal forces, which allows us to calculate its parameters.
This work was supported
by the grant of the President of Russian Federation MK-1371.2013.8.
References
1. Kraeva E.M. High-speed centrifugal pump units. Siberian Stat
Aerospace University – Krasnoyarsk, 2011. - 212 p.
2. Abramovich G.N. The theory of turbulent
jets.
- Moscow. : Fizmatgiz,1960. -716 p.
3. Van Dyke Milton. An Album of
Fluid Motion (10th ed.). Stanford: Parabolic Press, 1982.