Современные информационные технологии /1. Компьютерная инженерия

Аждер В.Д., Потапова М.С.

Московский технологический университет, Россия

Модель нейрона, находящегося под действием шума

Говоря об обработке сигналов, можно сказать, что не существует более плодородной области применения нейронных сетей (НС). Многие физические явления, отвечающие за генерацию информационных сигналов, встречаемых на практике, управляются нелинейной динамикой нестационарной и сложной природы, не имеющей точного математического описания. Для использования полного информационного содержания таких сигналов требуются:

1) нелинейность, которая делает возможным извлечение статистики высокого порядка из входного сигнала;

2) обучение к адаптации, посредством которой система может обучаться исследуемому физическому механизму среды и адаптироваться к непрерывным изменениям внешней среды;

3) механизм внимания, в котором с помощью самоорганизации система может сфокусировать свои вычислительные мощности на конкретном месте в пространстве для более детального анализа.

Пусть имеем линейный нейрон, получающий входной сигнал X от множества, состоящего из узлов-источников. Выход Y этого нейрона с учетом шума выражается соотношением

, (1)

где ω_i – i-й синаптический вес; N – шум обработки сигнала (рис.1).

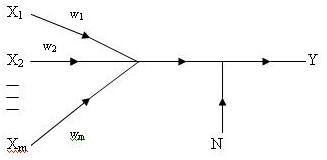
Рис.1. Граф передачи сигнала в зашумленном нейроне.

Предположим следующее:

1) выход нейрона Y представляет гауссовскую случайную величину с дисперсий ;

2) шум обработки сигнала N гауссовской случайной величины с нулевым средним и дисперсией ;

3) шум обработки является некоррелированным по всем своим входным составляющим, т.е. , .

Распределение Гаусса выходного сигнала Y можно обеспечить двумя способами. Входные сигналы X₁ , X₂ , …, X_m имеют распределение Гаусса. При этом предполагается, что аддитивный шум N также является гауссовским. Тогда гауссовское распределение выходного сигнала вытекает из того факта, что он является суммой гауссовских случайных величин. Как альтернатива, входные сигналы X₁ , X₂ , …, X_m могут быть независимо и равномерно распределены. В этом случае распределение их суммы становится гауссовским при . Это следствие центральной предельной теоремы.

Из теории информации известно, что взаимная информация I(X;Y) между непрерывными случайными величинами X и Y обладает следующим свойством:

, (2)

где h(X) – дифференциальная энтропия X,

h(X/Y) – условная дифференциальная энтропия X для данного Y, которая определяется следующим выражением:

,

где h(X,Y) – совместная дифференциальная энтропия X и Y.

Дифференциальная энтропия имеет вид:

,

где f_x(x) – формула распределения вероятности случайной величины X при соблюдении следующих условий:

1) ;

2) ;

3) , , где g_i(x) – некоторая функция от x.

Условие 3 определяет моменты X, которые зависят от способа определения функции g_i(x). В результате, условие 3 суммирует все априорные знания о случайной величине X.

Для того, чтобы определить распределение с максимальной энтропией, необходимо решить задачу условной оптимизации. Для решения этой задачи используем метод множителей Лагранжа. Сначала составим целевую функцию:

,

где λ₁, λ₂, … λ_m – множители Лагранжа.

Продифференцируем интеграл по f_x(x) и приравняем результаты к нулю:

.

Решение этого уравнения относительно неизвестной функции f_x(x) имеет вид:

. (3)

Множители Лагранжа в (3) выбираются в соответствии с условиями 2 и 3. Равенство (3) определяется распределением с максимальной энтропией.

Используя (2), запишем взаимную информацию I(X;Y) между выходом нейрона Y и входным вектором X следующим образом:

.

Из формулы (1) несложно заметить, что функция плотности вероятности переменной Y для входного вектора X равна функции плотности вероятности суммы константы и гауссовской случайной величины.

Следовательно, условная энтропия h(Y/X) является информацией, которую выходной нейрон Y накапливает о шуме обработки сигнала N, а не о самом векторе полученного сигнала X. Исходя из этого, примем

и перепишем выражение (2) в следующем виде:

(4)

Определим дифференциальную энтропию случайной величины h(Y). Для этого предположим, что известны среднее значение μ и дисперсия σ² случайной величины X.

По определению имеем:

.

Сравнивая это равенство с условием 3, видим, что

, .

Используя равенство (3), получим:

.

Подставляя это равенство в условие 2 и 3, а затем, разрешая результат относительно λ₀ и λ₁, будем иметь:

.

Таким образом, искомая формула f_x(x) имеет вид

.

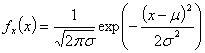Это плотность вероятности гауссовской случайной величины X со средним значением μ и дисперсией σ². Максимальное значение дифференциальной энтропии такой случайной величины имеет вид:

. (5)

Применяя выражение (5) к дифференциальной энтропии гауссовской случайной величины, получим:

(6)

и

(7)

После подстановки выражений (6) и (7) в формулу (4), и упростив результат, имеем:

,

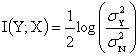где зависит от .

Частное можно рассмотреть как отношение сигнал/шум. Предполагая, что дисперсия фиксирована, можно заметить, что взаимная информация I(Y;X) достигает максимума при максимизации дисперсии выхода нейрона Y. Таким образом, можно утверждать, что при определенных условиях максимизации дисперсии выходного сигнала возможно максимизировать взаимную информацию между входным и выходным сигналами нейрона.

Литература:

1. Горбань А.Н., Россиев Д.А. Нейронные сети на персональном компьютере. - Новосибирск: Наука, 1996.

2. Николенко С. И., Тулупьев А. Л. Самообучающиеся системы. — Москва, МЦНМО, 2009.

3. Минаев Ю.Н., Филимонова О.Ю., Бенамеур Лиес. Методы и алгоритмы идентификации и прогнозирования в условиях неопределенности в нейросетевом логическом базисе. — М.: Горячая линия-Телеком, 2003.