К. ф.-м. н. Мирская Е.И., к. ф.-м. н. Марзан С.А.

Брестский государственный университет имени А.С. Пушкина,

Республика Беларусь

Исследование моментов сглаженной оценки спектральной плотности

Исследование статистических оценок спектральных плотностей является одной из классических задач анализа временных рядов. В настоящее время непараметрические методы анализа временных рядов широко применяются в различных областях науки и техники, таких как радиоэлектроника, медицина, экономика, астрономия.

Среди непараметрических методов спектрального оценивания одним из наиболее распространенных является метод Уэлча, в котором для построения оценки спектральной плотности производится осреднение периодограмм, построенных по пересекающимся интервалам наблюдений.

В данной работе обобщаются результаты, полученные Д. Бриллинджером, И.Г. Журбенко на произвольные окна просмотра данных.

В качестве оценки неизвестной взаимной спектральной плотности процесса построим и исследуем статистику вида

. (1)

Предположение 1. Пусть окна просмотра данных ограничены единицей и имеют ограниченную постоянной вариацию.

Теорема 1. Математическое ожидание оценки взаимной спектральной плотности ,, задаваемой соотношением (1), имеет вид

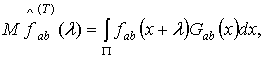(2)

,

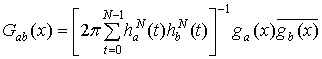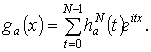
Доказательство. Учитывая свойства математического ожидания, получим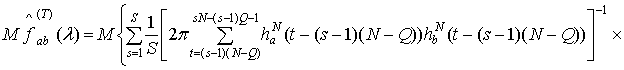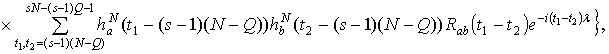используя соотношение, связывающее взаимную ковариационную функцию и взаимную спектральную плотность, запишем

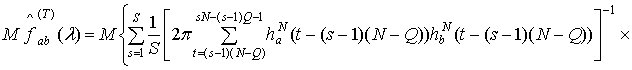
Меняя порядок суммирования и интегрирования, и сделав замену переменных получим требуемый результат.

Теорема 2. Если взаимная спектральная плотность непрерывна в точке и ограничена на , окна просмотра данных удовлетворяют предположению 1, то для оценки , заданной выражением (1), справедливо соотношение

(3)

Доказательство. Учитывая соотношение (2), запишем

Рассмотрим каждое из слагаемых. Учитывая, что функция непрерывна в точке и ограничена на

,

Теорема доказана.

Используя методику Бриллинджера Д., в качестве оценки неизвестной взаимной спектральной плотности исследуем статистику вида

(3)

где − спектральное окно, а − оценка взаимной спектральной плотности, заданная соотношением (1).

Теорема 3. Математическое ожидание сглаженной оценки взаимной спектральной плотности, , задаваемой соотношением (3), имеет вид

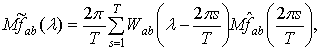
где − спектральное окно, а − оценка взаимной спектральной плотности, заданная выражением (1).

Теорема 4. Если взаимная спектральная плотность непрерывна в точке и ограничена на , окна просмотра данных удовлетворяют предположению 1, то для оценки , заданной выражением (3), справедливо соотношение

Доказательство. Используя свойства математического ожидания,

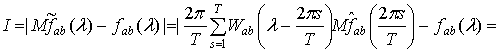
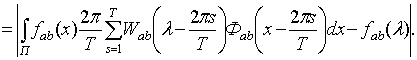
Откуда

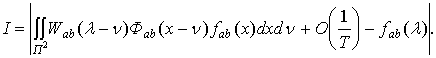
Сделаем замену переменных затем получим,

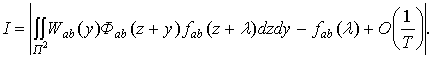
Учитывая, что свертка двух ядер является ядром,

ядро.

Следовательно,

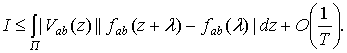
Полученное соотношение можно представить в виде

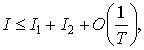
Рассмотрим каждый из интегралов. Так как взаимная спектральная плотность непрерывна в точке и, учитывая свойства ядерных функций, получим, что можно сделать сколь угодно малым за счет выбора

Так как ограничена на а является ядром,

Теорема доказана.