Наурызбаева
Р.М.
Академия Пограничной службы Комитета Национальной
безопасности Республики Казахстан, г. Алматы
ГЕОМЕТРИЧЕСКИЕ СВОЙСТВА КРИВЫХ
Геометрические и механические свойства кривых
используются в различных механизмах, деталях машин, строительных конструкциях,
в оптике, в изобразительном искусстве, в архитектуре, в теории и практике геометрических построений, в черчении и т. д. Некоторые кривые непосредственно реализуются в физических яв-
лениях, в природе и в обыденной жизни. Поэтому даже общее
знакомство с отдельными кривыми и их свойствами возбуждает особый интерес,
развивает математическое мышление и обогащает сознание многообразными связями
математической теории с конкретным
опытом. Одни из этих кривых интересны в теоретическом отношении,
другие находят практическое применение, третьи обладают оригинальными
особенностями формы, четвертые играли ту или иную роль
в истории математики.
В данной работе рассмотрим один из интереснейших фактов, касающийся площадей фигур ограниченых кривыми
в полярной системе координат.
Нам известно, что приняты два вида полярных координат:
1) строго полярные координаты, где ![]() ,
,
2) обобщенная полярная система координат, где как ![]() , так и
, так и ![]() .
.
Рассматрим полярные координаты первого вида.
Если существует уравнение кривой ![]() в полярной системе
координат, то ее можно рассматривать как функцию переменной
в полярной системе
координат, то ее можно рассматривать как функцию переменной ![]() , где
, где ![]() .
.
Лемма.
Если функция ![]() определена и непрерывна на отрезках
определена и непрерывна на отрезках ![]() , где Т-период данной функции, то площади ограниченные
, где Т-период данной функции, то площади ограниченные
графиком данной функции на этих промежутках
равны, где ![]() .
.
Доказательство. Графиком данной
функций замкнутые кривые, так область определения функции состоит из замкнутых отрезков, т.е. ![]() .
.
Как
известно, площадь фигуры ограниченной графиком функции ![]() на отрезке
на отрезке ![]() в полярной системе коодинат равна определенному
интегралу от функции
в полярной системе коодинат равна определенному
интегралу от функции![]() в пределах от
в пределах от ![]() до
до ![]() , как предел частичной интегральной суммы, т.е.
, как предел частичной интегральной суммы, т.е.
 ,
,
где ![]() ,
, ![]() .
.
При этом, если функция ![]() является
периодическая функция с периодом Т, то
функция
является
периодическая функция с периодом Т, то
функция ![]() так же является
функцией с периодом Т, хотя меньший период может оказаться не Т.
так же является
функцией с периодом Т, хотя меньший период может оказаться не Т.
Разобьем промежуток
![]() на п частей (Рис.1).
на п частей (Рис.1).
![]()
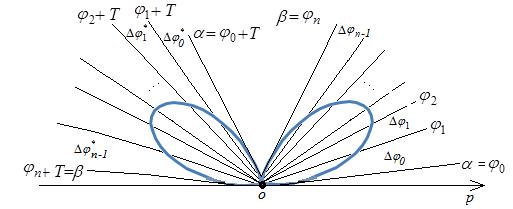
Рис.1
Возьмем, произвольным
образом, из каждого промежутка точки ![]() ,
, ![]() ,
, ![]()
Тогда в силу периодичности
данной функции ![]() получаем
получаем
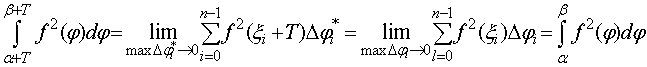 Лемма доказана.
Лемма доказана.
Теорема. Если ![]() непрерывная периодическая
функция с
периодом
непрерывная периодическая
функция с
периодом ![]() , то площади фигур, ограниченные графиками
функций
, то площади фигур, ограниченные графиками
функций ![]() и
и ![]() равны между собой, где
равны между собой, где
![]() (
(![]() множество натуральных чисел).
множество натуральных чисел).
Доказательство. Пусть сначала функция ![]() с периодом
с периодом ![]() определена на отрезке
определена на отрезке
![]() . График этой функций замкнутая кривая, так как по условию
теоремы функция
. График этой функций замкнутая кривая, так как по условию
теоремы функция ![]() периодическая функция с
периодом
периодическая функция с
периодом ![]() , т.е.
, т.е. ![]() .
.
И пусть площадь фигуры ограниченной графиком функций![]() , равна:
, равна:

где
![]() -одна из первообразных данной функции.
-одна из первообразных данной функции.
Если умножить аргумент функций ![]() на число
на число ![]() , то получаем функцию
, то получаем функцию ![]() с периодом
с периодом ![]() . Областью
определения этой функций является объединение
следующих отрезков.
. Областью
определения этой функций является объединение
следующих отрезков.
![]() Тогда
площадь фигуры ограниченных графиком функций
Тогда
площадь фигуры ограниченных графиком функций ![]() равна
равна 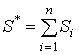 , где
, где ![]() площади фигур ограниченных графиками функций
площади фигур ограниченных графиками функций ![]() и лучами
и лучами ![]()
![]() ,
, ![]() .
.
При
помощи замены ![]() получаем:
получаем:
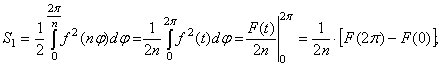
В
силу доказанной леммы
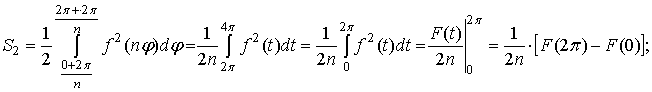 . . .
. . .
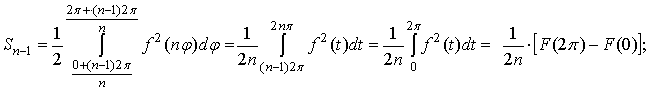 тогда
тогда
![]()
![]()
![]()
![]() ...
...![]()
![]() .
.
Следовательно
![]()
Пусть теперь функция ![]() с периодом
с периодом ![]() и пусть она
определена на отрезке
и пусть она
определена на отрезке ![]() . Графиком данной функций
являются замкнутая кривая, так как в этом промежутке функция не отрицательна,
т.е.
. Графиком данной функций
являются замкнутая кривая, так как в этом промежутке функция не отрицательна,
т.е. ![]() . Умножая аргумент функции
. Умножая аргумент функции ![]() на натуральное число
на натуральное число ![]() мы получаем функцию
мы получаем функцию ![]() .
.
Область
определения функции ![]() имеет вид:
имеет вид:
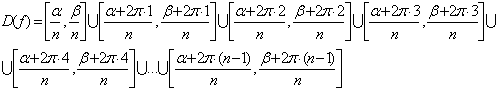 ( 3 )
( 3 )
Функция ![]() имеет период
имеет период ![]() , на каждом отрезке области определения график функции
замкнут.
, на каждом отрезке области определения график функции
замкнут.
Пусть площадь фигуры, ограниченной графиком
функции ![]() на
отрезке
на
отрезке ![]() имеет вид:
имеет вид:
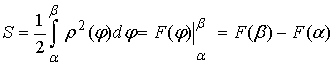
Тогда
площадь фигуры ограниченной графиком функции ![]() равна
равна
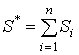 , где
, где ![]() - равные площади фигур ограниченных графиком функции
- равные площади фигур ограниченных графиком функции ![]() на
каждом отрезке из (3), т.е.
на
каждом отрезке из (3), т.е.
![]()
![]()
![]()
![]() ...
...![]()
![]() .
.
Действительно, в силу доказанной
леммы и замены получаем 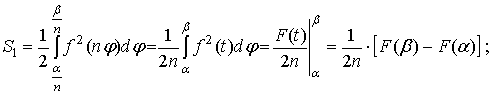
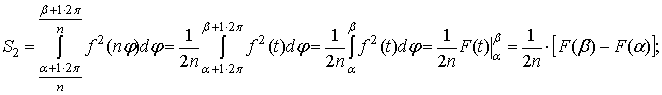 . . .
. . .
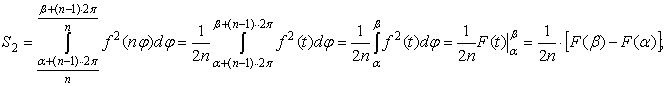 Следовательно,
Следовательно,
![]()
Теорема
доказана.
Пример. Найти площадь фигуры ограниченной графиком функций в полярной ![]() системе координат.
системе координат.
Решение: Чтобы найти площадь фигуры
ограниченной графиком функции ![]() в полярной системе координат,
нам достаточно найти площадь фигуры ограниченной графиком
функций
в полярной системе координат,
нам достаточно найти площадь фигуры ограниченной графиком
функций ![]() в силу доказанной теоремы.
в силу доказанной теоремы.
Найдем
область определения функции ![]() Для этого решаем
неравенство
Для этого решаем
неравенство ![]() . Отсюда
. Отсюда ![]() . Следовательно,
. Следовательно, ![]()
Далее
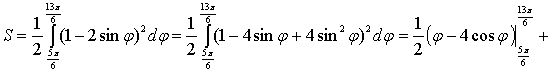
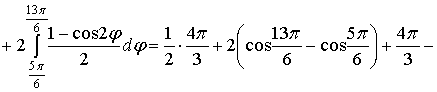
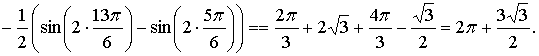
Покажем, что площадь фигуры,
ограниченной графиком функции ![]() в полярной системе координат также
равна этому значению
в полярной системе координат также
равна этому значению ![]() . Аналогично, имеем, что область
опрделения функции
. Аналогично, имеем, что область
опрделения функции ![]() .
.
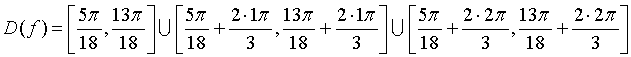
или 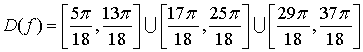 (Рис.2).
(Рис.2).
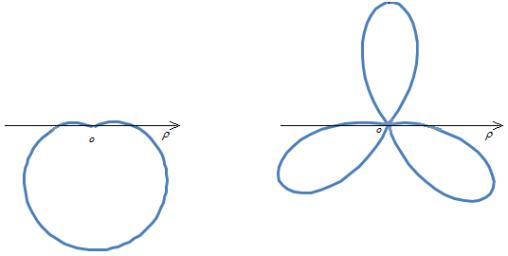
Рис.2
Период функции ![]() равна
равна ![]() Тогда можно вычислить площадь в
каждом отрезке области определения в отдельности.
Тогда можно вычислить площадь в
каждом отрезке области определения в отдельности.
Например, площадь в первом отрезке: 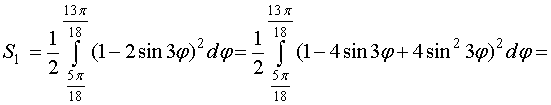

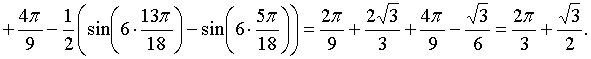
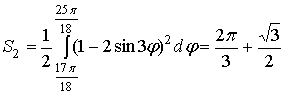 ,
, 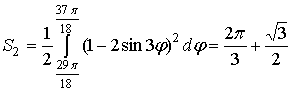 .
.
![]()
![]()
![]() .
.
Из последнего видно, что значения
площади фигур ограниченных графиками функций ![]() и
и ![]() , равны.
, равны.
Литература
1. Наурызбаева Р.М. Исследование функций в полярной системе координат
// Материалы VI международной
научно-практической конференции «Новини
на научния прогресс – 2010», София , 17-25 августа. С. 52-53.
2. Наурызбаева Р.М. Полярлық координаталар
жүйесінде функцияны зерттеу // Ғылыми-зерттеу жұмысы. –
Алматы, 2010. – 165 бет.