Математика /4. Прикладная математика

Ганенко А.С., к.ф.-м.н. Баландин В.А., Аждер Т.Б.

Московский технологический университет, Россия

Устранение шумов в ЭКГ при помощи вейвлет-преобразования

Современная медицинская диагностика – сложный процесс получения достоверных и точных знаний. В этой связи одной из проблем является улучшение и повышение качества результатов исследований. Электрокардиография является одним из самых точных методов в медицинской диагностике. Это связано с тем, что электрокардиограмма является основным показателем, который в настоящее время позволяет вести профилактический и лечебный контроль сердечнососудистых заболеваний. Однако часто полученные изображения сигналов бывают зашумленными, что является существенной помехой при выявлении заболеваний и установки верного диагноза. Для анализа таких сигналов нужен такой метод, который может обеспечить хорошее разрешение по частоте и по времени. Первое необходимо для локализации низкочастотных составляющих, а второе – для разрешения компонент высокой частоты.

При вейвлет-анализе сигнал раскладывается на аппроксимирующие (низкочастотные) коэффициенты, которые представляют сглаженный сигнал, и детализирующие (высокочастотные) коэффициенты, описывающие колебательные процессы. Следовательно, шумовая компонента больше отражается в детализирующих компонентах d_i. Поэтому при удалении шума обрабатывают, как правило, детализирующие коэффициенты. Второе предположение заключается в том, что шумовая компонента представляет собой сигнал, меньший по модулю, чем основной. Поэтому простейший способ удаления шума состоит в том, чтобы сделать нулевыми значения коэффициентов, меньших некоторого порогового значения. Эта процедура называется пороговой обработкой (thresholding) коэффициентов. Широкое распространение получили такие методы пороговой обработки, как жесткий thresholding и мягкий thresholding . [1]

При жесткой пороговой обработке сохраняются неизменными все коэффициенты, больше или равные по абсолютной величине порога τ, а меньшие коэффициенты обращаются в нуль. При мягкой пороговой обработке наряду с обращением в нуль коэффициентов, по модулю меньших, чем τ , происходит уменьшение по модулю остальных коэффициентов на величину τ.

При решении задачи шумоподавления необходимо: оценить спектральный состав шумовой компоненты, выбрать тип пороговой обработки и критерий расчета самого порога.[2]

От выбора порогового уровня фона (оценка дисперсии шума) зависит качество шумоподавления сигнала, оцениваемое в виде отношения сигнал/шум. Задание малых значений порога сохраняет фон в коэффициентах детализации и поэтому приводит лишь к незначительному увеличению отношения сигнал/шум. При больших значениях порога можно потерять коэффициенты, которые несут существенную информацию. Поиск оптимального значения τ₀ означает отыскание такого порога, который при наименьшем смещении восстановленного сигнала обеспечивает наибольшее значение отношения сигнал/шум.

Качество шумоподавления сигнала (отношение сигнал/шум) зависит также от способа применения пороговой обработки:

· общий thresholding, осуществляется с использованием фиксированного значения порога τ – значения, единого для всех уровней и коэффициентов детализации сигнала;

· многоуровневый thresholding, осуществляется с использованием порога τ, значения которого изменяются от уровня к уровню;

· локальный thresholding, подразумевает использование порога τ, переменного не только по уровню разложения, но также зависящего от позиции коэффициентов детализации на данном уровне.

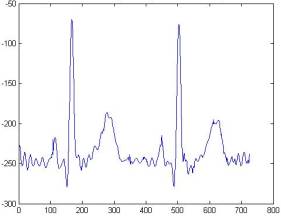
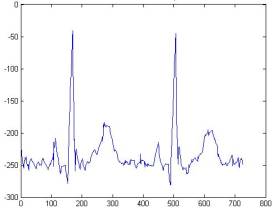
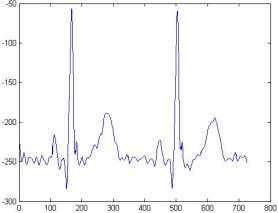
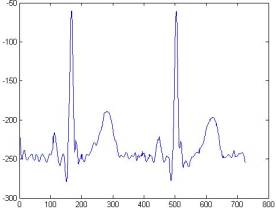
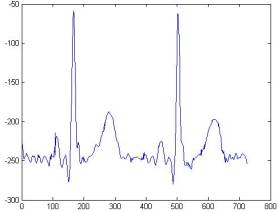
Результаты очистки сигнала ЭКГ

Ниже представлены результаты очистки сигнала ЭКГ с помощью следующих вейвлетов:

· Дискретные аппроксимации вейвлетов Мейера;

· Биортогональные вейвлеты;

· Дуальные биортогональные вейвлеты;

· Вейвлеты Добеши 2,4,6 и 8-го порядков;

Рисунок 1. Сигнал, очищенный с использованием дискретных апроксимаций вейвлетов Мейера.	Рисунок 2. Сигнал, очищенный с использованием биортогональных вейвлетов.
Рисунок 3. Сигнал, очищенный с использованием дуальных биортогональных вейвлетов.	Рисунок 4. Сигнал, очищенный с использованием вейвлета Добеши 2-го порядка.
Рисунок 5. Сигнал, очищенный с использованием вейвлета Добеши 4-го порядка.	Рисунок 6. Сигнал, очищенный с использованием вейвлета Добеши 6-го порядка.
Рисунок 7. Сигнал, очищенный с использованием вейвлета Добеши 8-го порядка.	Рисунок 8. Сигнал, очищенный с использованием вейвлета Хаара.

В качестве критериев отбора рассматривалась форма зубцов, их величина, а также остаточная зашумленность сигнала. Сравнение проводилось как между сигналами, очищенными при помощи различных вейвлетов, так и с моделью идеального комплекса PQRST.

Наиболее адекватным сигналом, соответствующим модели комплекса PQRST был выбран сигнал, очищенный вейвлетом Добеши 8-го порядка. В нём действительно четко прослеживаются все зубцы комплекса, а также в нем содержится наименьшее количество шума.

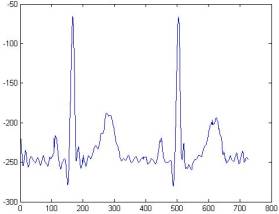
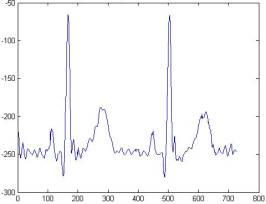
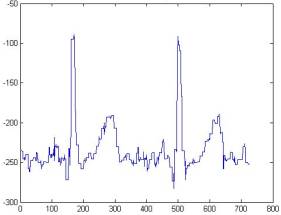
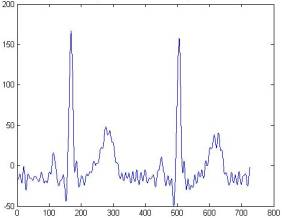
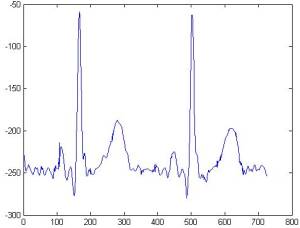
Сравнение сигнала из базы Physionet с сигналом, очищенным вейвлетом Добеши 8-го порядка

На рисунках 9 и 10 представлены кардио-сигналы, очищенные с помощью методики, использованной в базе Physionet (рисунок 9), а также с помощью вейвлета Добеши (рисунок 10).

Рисунок 9

Рисунок 10

Из рисунка следует, что очистка сигнала с помощью вейвлета Добеши более эффективна, чем предложенная ресурсом Physionet. Действительно, если зубцы P, Q, R выглядят одинаково хорошо на двух предложенных графиках, то зубцы S и T на рис.10 определяются неоднозначно из-за присутствия шумов.

Литература:

1. Смоленцев Н.К. Основы теории вейвлетов. Вейвлеты в MATLAB. – М.:ДМК Пресс, 2008.

2. Misiti M., Misiti Y.: Wavelet ToolboxTM 4 User’s Guide ⓒ COPYRIGHT 1997–2009 by The MathWorks, Inc.

3. Ресурс для медико-биологических исследований и разработок https://physionet.org.