PORE-SCALE DIRECT NUMERICAL SIMULATION OF SINGLE PHASE FLOW IN POROUS MEDIA

Kudaikulov A.A.

al-Farabi Kazakh National University, Almaty, Kazakhstan

e-mail: aziz.kudaikulov@gmail.com

Abstract. The paper presents the results of mathematical and numerical modeling of single-phase fluid flow in porous media with periodic microstructure. Object of study is the area in which the cylinders are arranged in a periodic manner. At the boundaries of the area for the flow parameters is set periodic boundary condition. Also in the paper presents comparison with Darcy’s law and the calculation of the permeability coefficient for different values of the radius of the cylinders.

Keywords: porous medium with periodic microstructure, Navier-Stokes equation, Darcy’s law, permeability of porous medium.

In most cases [1] the Darcy's law is used to determine parameters of single phase fluid flow in porous medium, which relates filtration rate and pressure gradient as:

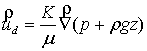,                                         (1)      

where - permeability of porous medium,  - fluid viscosity,  - filtration rate,  - pressure in the porous medium and   - hydrostatic pressure. The main advantage of  Darcy's law is that, if we know the values ​​of the permeability of the porous medium -  , then we can determine the flow parameters of the fluid in the porous medium for large scale (Area is about 1  and depth is about 100 ). But in most cases calculation the permeability -  is very difficult problem. The permeability - K is the macroscopic parameter of porous medium, which characterized the structure of the porous medium (geometrical details of the porous medium at the pore-scale and other physical parameters such as viscosity). To exactly calculate the permeability - , we need to know properties of the porous medium at the pore-scale. Nevertheless, new experimental technologies and high-resolution imaging for porous media [3,4] can provide three-dimensional structural details of porous materials with resolution  in one micron. But the permeability -  does not only depend on the geometrical details of the porous medium, it is also depends on physical properties of the porous medium and it varies from one case to another. Therefore to exactly calculate the macroscopic parameters of the fluid flows in the porous medium, we need to simulate fluid flow in the porous medium at the pore-scale. There exist many pore-scale models of the fluid flows in the porous medium such as Lattice-Boltzmann, pore network models, discrete particle methods (smoothed particle hydrodynamics) and direct discretization methods (standard finite element, finite volume, immersed boundary methods). All of these methods require high computational power and all of these methods, except direct discretization methods, are not exact. Direct discretization methods, it is methods that discretize the Navier-Stokes equations and solve these for domain with complex geometries. The main advantages of the direct discretization methods is that can be applied for the domains with complex geometries and simulate fluid flow in the porous medium more exactly than others. These advancements such as development of advanced numerical methods and high resolution imaging techniques are now helping researchers to make progress in the understanding of pore-scale processes and how they influence fluid transport at macroscopic scale. This paper presents the pore-scale direct numerical simulation of single phase flow in porous media with periodic microstructure. This simulation based on the Navier-Stokes equations for incompressible single phase fluid:

,                (2)

,                                                         (3)

where - density of the fluid,  – velocity of the fluid flow,  – pressure, – fluid viscosity and  – acceleration due to gravity. These equations are system of non-linear partial differential equations and the non-linear term renders it difficult to solve analitically. It is usually a convenient way to non-dimensionalize the variables by introducing scaling factors. Let the velocity  scales with the characteristic velocity - ,  - scales with  where  is a characteristic length, time  scales with . Then, the dimensionless variables become:

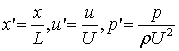                                    (4)

On substituting the primed variables into equations (2) and (3) and rearranging the terms and dropping the primes, we obtain:

,               (5)

,                                                         (6)

Further we consider the equations (5) and (6) instead of (2) and (3). The main difficulty of the pore-scale modeling of the fluid flow in the porous medium is that it is very difficult to set the correct boundary and initial conditions for the system of equations (5) and (6). The paper [8] has proof  of that the system of equations (5) and (6) has a solution and it is unique and depends continuously on initial and boundary conditions if zero initial condition for the velocity and periodic boundary conditions for the velocity and pressure are applied. In cases, when need  to define more complex initial and boundary conditions for the velocity and pressure, we can measure these experimentally [3,4]. In this paper the zero initial condition for the velocity and periodic boundary conditions for the velocity and pressure are considered. Analytical solution of the system of the equations (5) and (6) was found only in special cases and for simple domains. Therefore, to solve the system of equations (5) and (6) need to use numerical methods. In this paper a finite volume method with adaptive mesh refinement is used to discretize the Navier-Stokes equations (2) and (3). To solve these discretized equations, MAC (Marker-and-Cell) method is used [5,6,7].

          This paper considers two-dimensional rectangular domain with size  (where  changes from  to  and  changes from  to ), in which the cylinders are arranged in a periodic manner (figure  1). The initial condition for the velocity is defined as follows:

.                                                     (7)

Boundary conditions for the velocity and pressure are as follows:

1)     At the boundaries of the area:

,

,                              (8)

,

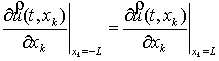2)     On the surface of the cylinders (no-slip condition):

,                                                     (9)

where  – number of dimensions, in our case - .

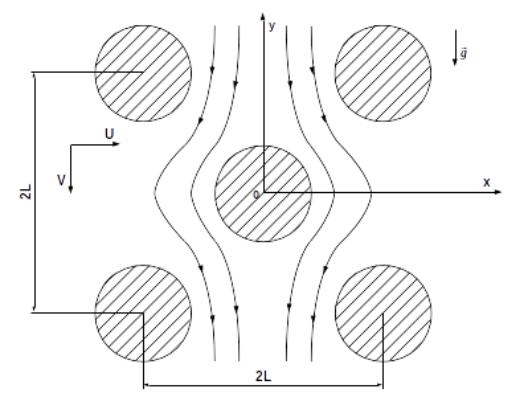
Figure 1: Two-dimensional rectangular domain with size  (where  changes from  to  and  changes from  to ), in which the cylinders are arranged in a periodic manner

In order to find the rate of filtration -  need to average the velocity over the volume:

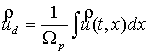,                                         (10)

where  – volume of the pore space [1]. Further, from Darcy's law (1) we can find the permeability of the porous medium:

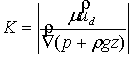                                             (11)

 

 

Results:

1) Case when radius of cylinders -  = 0,1

0,1

-2,25

0,5

-0,593

1

-0,296

2

-0,138

5

-0,0583

10

-0,0297

 

Table 1: Relation between fluid viscosity -  and filtration rate -  for case when radius of cylinders - = 0,1

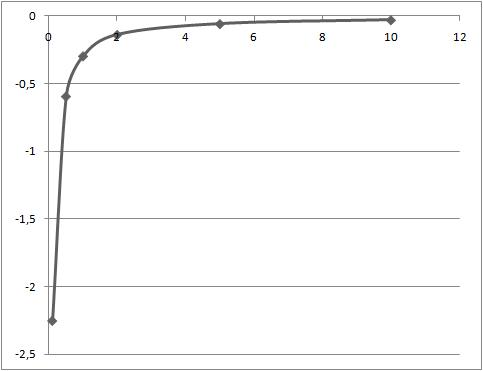
Figure 2: Relation between fluid viscosity -  and filtration rate -  for case when radius of cylinders - = 0,1

2) Case when radius of cylinders -  = 0,15

0,1

-1,53

0,5

-0,334

1

-0,171

2

-0,083

5

-0,0356

10

-0,0171

 

Table 2: Relation between fluid viscosity -  and filtration rate -  for case when radius of cylinders - = 0,15

 

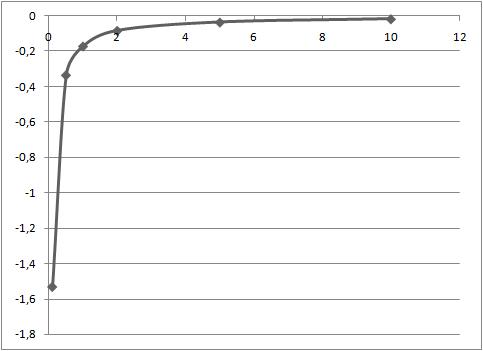
Figure 3: Relation between fluid viscosity -  and filtration rate -  for case when radius of cylinders - = 0,15

3) Case when radius of cylinders -  = 0,2

0,1

-0,91

0,5

-0,163

1

-0,084

2

-0,04

5

-0,019

10

-0,0092

 

Table 3: Relation between fluid viscosity -  and filtration rate -  for case when radius of cylinders - = 0,2

 

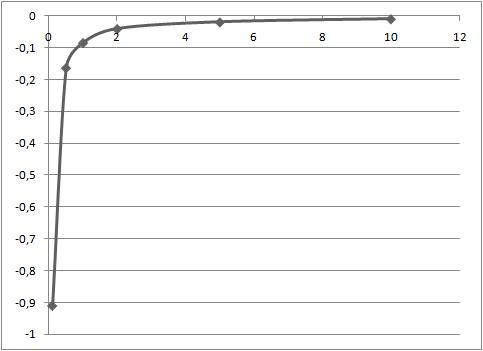
Figure 3: Relation between fluid viscosity -  and filtration rate -  for case when radius of cylinders - = 0,2

References

1.     Bear J., Cheng A.H.-D. Modeling Groundwater Flow and Contaminant Transport, Theory and Applications of Transport in Porous Media, Springer, Volume 23, 2010.

2.     Cannon J.R., Knightly G.H. A note on the Cauchy problem for the Navier-Stokes equations, SIAM Journal on Applied Mathematics, Vol. 18, No. 3, 1970, pp. 641-644.

3.     Karadimitriou N.K. Two-phase flow experimental studies in micro-models, Utrecht, Netherland, 2013.

4.     Li D. Encyclopedia of Microfluidics and Nanofluidics, Springer, 2008.

5.     Louis H. H., John B. B. An Adaptive Mesh Projection Method for Viscous Incompressible Flow, SIAM Journal on Scientific Computing 18(4):996-1013, 1997.

6.     Popinet S. Gerris: a tree-based adaptive solver for the incompressible Euler equations in complex geometries, Journal of Computational Physics 190(2):572-600, 2003.

7.     Sidilkover D., Ascher U. M. A Multigrid Solver for the Steady State Navier-Stokes Equations Using The Pressure-Poisson Formulation, Comp. Appl. Math 14:21-35, 1995.

8.     Yoshikazu Giga, Alex Mahalov and Basil Nicolaenko The Cauchy problem for the Navier-Stokes equations with spatially almost periodic initial data, Department of Math., Hokkaido Univ., 2004, Preprint Series # 683