К.т.н. доцент Абрамов П.Б.

ВУНЦ ВВС «ВВА имени проф. Н.Е.Жуковского и Ю.А.Гагарина»

г.Воронеж, Россия

Обоснование возможности применения марковских моделей

для моделирования немарковских процессов

В настоящее время моделирование динамики сложных систем, в том числе систем массового обслуживания (СМО), приобретает все большую актуальность. Одним из хорошо известных и широко применяемых подходов в данной области является математический аппарат марковских цепей. Марковским моделям посвящено большое количество классических работ, например [1-3].

Для моделирования динамики систем с учетом последействия успешно применяются полумарковские модели. Они хорошо обоснованы в известных трудах, к основным из которых можно отнести [4,5]. Полученные авторами соотношения весьма сложны, включают в себя кратные суммы и интегралы. Для моделей с количеством состояний больше десяти разработать полумарковскую модель весьма затруднительно.

В данной статье рассмотрен метод моделирования стационарного режима динамики сложных систем, основанный на замене рекуррентных потоков событий простейшими, с пересчетом их интенсивностей. Он является дальнейшим развитием и обобщением классического метода фаз Эрланга [2]. Распределение времени как случайной величины между событиями в потоке Эрланга описывается гамма-распределением с целочисленным параметром. Порядок потока оценивается на основе выборки случайного процесса, согласно выражению:

, (1)

где m – математическое ожидание, а σ – среднеквадратическое отклонение значения временного интервала между событиями в стохастическом потоке. После этого достаточно ввести на соответствующем переходе графа К_э-1 псевдосостояний, увеличив в К_э раз интенсивности потоков событий на вновь полученных дугах графа состояний системы, чтобы модель стала марковской. Пример подобного подхода для модели СМО приведен на рисунке 1.

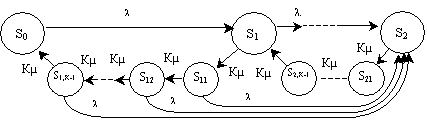
Рисунок 1 – Граф состояний одноканальной СМО с очередью в одно место

Для полученного графа вполне обоснованно могут быть составлены и решены уравнения Колмогорова-Чепмена, а затем рассчитаны вероятности состояний для немарковского процесса согласно выражению:

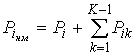. (2)

Следует отметить, что подобный подход осложняется целым рядом затруднений, в силу чего не получил широкого распространения. Прежде всего, при расчете порядка потока по формуле (1) вероятнее всего будет получено не целое значение. Кроме того, при больших значениях последействия существенно увеличивается количество уравнений модели.

Для изложения существа рассматриваемого в статье метода следует выделить структуру, включающую в себя состояние S₁ и связанные с ним псевдосостояния. Она приведена на рисунке 2.

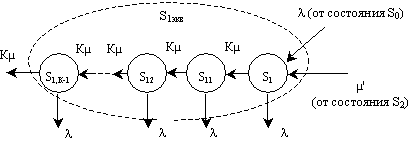
Рисунок 2 – Структура, включающая в себя состояние S₁

и связанные с ним псевдосостояния

Автором в ряде трудов [6-8] доказано, что данная марковская форма, взятая в отдельности, обладает целым рядом замечательных особенностей. Так, отношения вероятностей любых состояний, входящих в подобную форму в стационарном режиме не зависят от интенсивности входящего в форму потока. Тогда вся марковская форма (рис.2) может быть в стационарном режиме представлена в виде единственного состояния, только интенсивности исходящих из формы потоков должны быть пересчитаны. Доказано, что коэффициент пересчета не зависит от конфигурации внешней по отношению к марковской форме (рис.2) марковской цепи. Коэффициенты пересчета интенсивностей рекуррентных потоков к интенсивностям простейших потоков К_коррПД , полученные на модели первого приближения приведены в монографии [8].

Дальнейшие исследования показывают, что в модели первого приближения при пересчете не в достаточной мере учитывается фактор временной задержки событий в рекуррентном потоке. Поэтому определение коэффициента пересчета интенсивности потока целесообразно проводить на полумарковской модели цепи, которая является простейшим замыканием для исследуемого потока с последействием и других исходящих из данного состояния потоков. Все прочие потоки полагаются простейшими с произвольной интенсивностью.

Численными методами рассчитываются стационарные вероятности состояний. Затем путем решения обратной задачи вычисляется интенсивность простейшего потока, который доставит те же стационарные вероятности состояний. Отношение полученной интенсивности простейшего потока к интенсивности исследуемого потока с последействием даст коэффициент коррекции. Теоретические доказательства независимости полученного коэффициента от конфигурации замыкающей данное состояние цепи остаются справедливыми, поэтому полученный результат может быть использован в более сложных моделях для пересчета интенсивностей рекуррентных потоков к простейшим и оценки стационарных вероятностей состояний.

Покажем, как данный метод позволяет учесть влияние последействия на значения параметров СМО. В качестве примера рассмотрим модель одноканальной СМО с ожиданием. Будем полагать интенсивность рекуррентного потока обслуживания равной μ, а интенсивность простейшего потока заявок равной λ. Распределение временного интервала в рекуррентном потоке положим подчиняющимся закону Эрланга порядка K_пд. Некоторые значения коэффициентов пересчета интенсивности рекуррентного потока К_коррПД , полученные на полумарковской модели, приведены в таблице 1.

Таблица 1 – Значения коэффициента К_коррПД для интенсивностей потоков

Нагрузка ρ = λ/µ	Коэффициент последействия в рекуррентном потоке Kпд
	2	3	4	5	6	7
0	0,5000	0,3333	0,2500	0,2000	0,1666	0,1428
0,05	0,4878	0,3172	0,2320	0,1810	0,1470	0,1228
0,10	0,4762	0,3021	0,2155	0,1638	0,1296	0,1054
0,15	0,4651	0,2880	0,2003	0,1483	0,1142	0,0904
0,20	0,4545	0,2747	0,1863	0,1344	0,1007	0,0771
0,25	0,4444	0,2623	0,1734	0,1218	0,0888	0,0663
0,30	0,4348	0,2506	0,1616	0,1106	0,0784	0,0569
0,35	0,4255	0,2397	0,1508	0,1005	0,0693	0,0488
0,40	0,4167	0,2294	0,1408	0,0914	0,0613	0,0419
0,45	0,4081	0,2201	0,1315	0,0832	0,0543	0,0361
0,50	0,4000	0,2105	0,1231	0,0758	0,0481	0,0311

Зададимся последействием К_э=2. Тогда следует использовать первый столбец таблицы 1, на основе которого и приводить интенсивность рекуррентного потока к интенсивности простейшего потока обслуживаний. После этого можно применять известные формулы оценки параметров СМО.

Результаты были сопоставлены с оценками вероятности отказа СМО без учета последействия. Графики зависимостей коэффициента коррекции вероятности отказа СМО К_{коррСМО} от нагрузки системы при различном количестве мест в очереди n приведены на рисунке 3. Зависимости имеют вид ломаных, поскольку применялась линейная аппроксимация промежуточных значений.

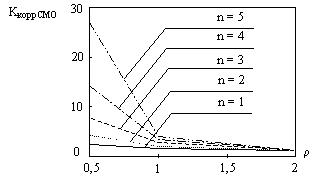
Рисунок 3 – Зависимость коэффициента коррекции K_{коррСМО}

вероятности отказа СМО от нагрузки ρ при различной длине очереди n

При нагрузках ρ>2 вероятность отказа СМО превышает 0,5, поэтому анализ подобных режимов не имеет смысла с практической точки зрения. Наиболее важны режимы работы системы, когда нагрузка составляет величину порядка от ρ=0,5 до ρ=2. Например, для числа мест в очереди, равном 5, и ρ=0,5 коэффициент коррекции вероятности отказа СМО составляет 27,08, что повышает вероятность отказа с пренебрежимо малой величины 8·10^-3 до вполне заметного значения 0,213. Полученные результаты находят также практическое подтверждение, поскольку из инженерного опыта проектирования вычислительных систем известна целесообразность обеспечения 20-25% запаса пропускной способности СМО.

Сформулируем основной вывод. Метод, основанный на пересчете интенсивностей рекуррентных потоков, позволяет вполне успешно разрабатывать марковские модели немарковских процессов для оценки параметров сложных систем. Особенно важным является возможность получения подобных результатов для нецелочисленных значений последействия в потоках, чего не позволяет достигнуть метод фаз Эрланга.

Литература

1. Таха, Хемди А. Введение в исследование операций. 7-е издание / Пер. с англ. М.: Издательский дом "Вильяме", 2005. 912 с.

2. Вентцель Е.С. Исследование операций. М.: Советское радио, 1972. 552 с.

3. Кеиени Дж., Снелл Дж. Конечные цепи Маркова / Пер. с англ. М.: Наука. 1970. 271 с.

4. Гнеденко Б.В., Коваленко И.Н. Введение в теорию массового обслуживания. М.: Наука, 1987. 336с .

5. Тихонов В.И., Миронов М.А. Марковские процессы. М.: Сов.радио,1977. 488 с.

6. Абрамов П.Б. Модели систем массового обслуживания на основе марковских форм с внешними потоками событий // Вестник Воронежского Государственного технического университета, 2012. Том 8. №6. С.109-112.

7. Абрамов П.Б., Чурсин М.А. Анализ существования и устойчивости решения для марковских моделей разомкнутых систем массового обслуживания // Вестник ВГУ, Серия: Системный анализ и информационные технологии, 2012. №1. С.56-61.

8. Абрамов П.Б. Основы теории марковских форм с внешними потоками событий [Текст]: монография. Воронеж: Издательско-полиграфический центр «Научная книга», 2014. 185 с.