Ефремова О.И., к. ф.-м. н. Иванисова О.В., к. ф.-м. н. Лукащик Е.П.

Кубанский государственный университет, Россия

Воздействие ступенчатого порыва на массивную пластину в ограниченной сжимаемой среде

ВВЕДЕНИЕ

В первых работах по апериодическому движению в сжимаемой жидкости принимался апериодический характер отклика системы «акустическая среда – пластина» на ступенчатое воздействие. Этот результат, справедливый для случая несжимаемой жидкости, был необоснованно перемещен на сжимаемую жидкость, что противоречит волновому характеру распространения возмущений в сжимаемой среде. Данное обстоятельство потребовало более детального изучения вопроса о характере переходных аэродинамических процессов в сжимаемой жидкости и в особенности с учетом влияния экрана, тем более, что в ряде работ [1,2] на основе асимптотических теорий был установлен колебательный характер переходных процессов.

ПОСТАНОВКА ЗАДАЧИ

Взаимодействие тонкой массивной пластины с ограниченным слоем сжимаемой жидкости описывается смешанной краевой задачей для потенциала возмущенных скоростей , включающей уравнения течения сжимаемой жидкости и уравнение динамики твердой пластины. В безразмерных величинах (за единицу скорости принимается скорость звука с, а за единицу длины – полудлина пластины a) эта задача имеет вид:

,

(1)

.

Здесь f – перемещение центра масс пластины, h – расстояние до твердой границы, m – относительная масса пластины, P – реакция сжимаемой среды. При центральном ударе вертикальная скорость на пластине задается законом: , где H(t) – функция Хэвисайда.

Представляется удобным дальнейшие преобразования проводить в терминах функции , которую с физической точки зрения можно рассматривать как интенсивность вихревого слоя, моделирующего влияние пластины на акустическую среду. Согласно интегралу Коши-Лагранжа перепад давления вдоль пластины определится как

. (2)

Выполнение условия Майскнера в виде требования непрерывности и ограничения давления приводит к равенствучто можно трактовать как требование бесциркуляционности течения. Суммарная гидродинамическая нагрузка на пластину определяется соотношением:

(3)

Применением интегрального исчисления в пространстве обобщенных функций (подробное изложение методики можно найти в работах [3]) смешанная краевая задача сводится к интегральному уравнению с разностным ядром в образах по Лапласу по временной переменной:

, (4)

где .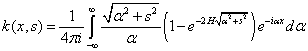

Укажем два подхода к вычислению ядра интегрального уравнения.

Во-первых, применением основных соотношений и интегральных представлений для бесселевых функций, можно получить выражение через функции Макдональда:

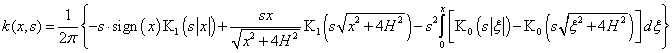
Во-вторых, представление ядра в форме интеграла Фурье наглядно указывает на его особенности, которые необходимо учитывать при выборе контура интегрирования в комплексной плоскости. Использование методов теории функций комплексной переменной приводит к выражению для ядра в виде интеграла с экспоненциально убывающим весом, что благоприятно сказывается на скорости численных расчетов:

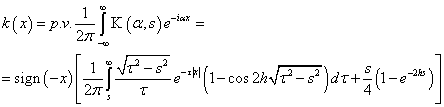. (5)

УЧЕТ ВЛИЯНИЯ МАССЫ

Определение влияния массы на характер переходного процесса в ограниченной сжимаемой среде можно проводить на основе следующего приближенного подхода. Вначале введем обозначение

, (6)

тогда для передаточной функции верно выражение:.

Пусть при правой части уравнения (4) равной единице. При ступенчатом воздействии для . В случае произвольных значений массы учитывая линейность задачи для определения можно предложить следующее приближенное соотношение: , или . Для передаточной функции тогда получим выражение:

, (7)

которое помогает наглядно оценить влияние относительной массы на величину гидродинамической силы.

В случае несжимаемой жидкости величину интерпретируют как коэффициент присоединенных масс.

Из формулы (7) следует, что учет влияния смещения центра масс существенен для относительно легких тел в плотной среде. При относительно больших по массе несущих поверхностях можно ограничиться решением чисто гидродинамической задачи, соответствующей случаю .

ЧИСЛЕННОЕ РЕШЕНИЕ

Решение сингулярного интегрального уравнения (4) в классе функций, неограниченных на кромках пластины, проводим методом дискретных вихрей [4]. Дискретизация уравнения (4) и условия Майскнера приводит к системе линейных алгебраических уравнений:

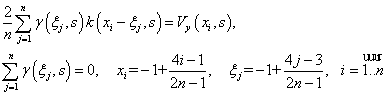(8)

Получив дискретное задание передаточной функции , аппроксимируем затем ее дробно-рациональной функцией . Коэффициенты аппроксимирующей функции находим с помощью метода наименьших квадратов. Корни полинома в знаменателе получаются комплексно-сопряженными, что характеризует переходной процесс как колебательный. Вещественная составляющая корней является положительной, что подтверждает затухающий характер колебаний.

Применение обратного преобразования Лапласа к аппроксимирующей функции приводит к аналитическому выражению переходной функции .

РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ

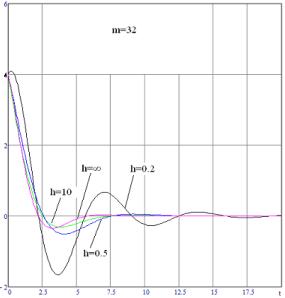
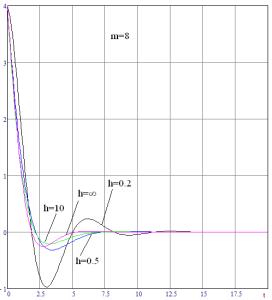
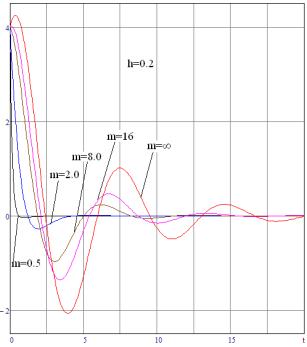
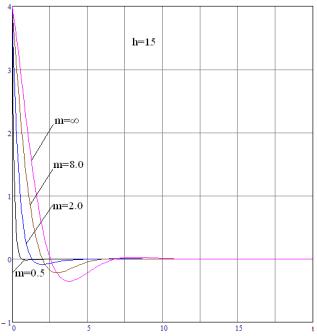
Основным отличием полученного для сжимаемой среды результата от соответствующего решения для несжимаемой жидкости состоит в том, что кроме сил, находящихся в фазе с ускорением и считающимися проявлением так называемых «присоединенных масс» газа, появляются демпфирующие силы в фазе со скоростью. Уменьшение относительной массы сопровождается уменьшением демпфирующих сил (рис.1). Колебательность переходных характеристик возрастает при приближении пластины к твердой границе (рис.2). Эффект появления демпфирующих составляющих в реакции акустической среды был отмечен и для движущейся пластины [5].

ЛИТЕРАТУРА

1. Юнов С.В. Апериодическое движение тонкого профиля в сжимаемой жидкости на малых отстояниях от твердой границы// Динамика сплошной среды с нестационарными границами. Чебоксары: Изд-во Чуваш. ун-та, 1984, – с. 113-117.

2. Ефремов И.И., Лукащик Е.П., Хуако Н.М. Нестационарное обтекание тонкого профиля дозвуковым потоком газа вблизи твердой границы // Прикладные проблемы механики жидкости и газа. Севастополь, 1994, – с.20-21.

3. Лукащик Е.П. Применение обобщенных функций в динамических контактных задачах аэроупругости крыла// Известия Саратовского университета. Серия: Математика. Механика. Информатика. Том 12. Вып 1, 2012, – с.69-80.

4. Белоцерковский С.М., Скрипач Б.К., Табачников В.Г. Крыло в нестационарном потоке газа. М: Наука. 1971. – 768с.

5. Лукащик Е.П., Ефремова О.И. Исследование переходных аэродинамических процессов методами теории автоматического управления // Экологический вестник научных центров ЧЭС. 2013. №4. Т. 1. – С.80-90.

a)

b)

Рисунок 1. Влияние массы пластины на переходные характеристики

a)

b)

Рисунок 2. Влияние близости твердой границы на переходные характеристики