Педагогические науки/5. Современные методы
преподавания.
К.п.н. Будахина Н.Л.
Ярославский государственный педагогический
университет, Россия
Практико-ориентированное обучение прикладной экономике бакалавров
по направлению «Профессиональное обучение (экономика и управление)»
В
настоящее время подготовке студентов предъявляются высокие требования в связи с возросшей потребностью в специалистах
высокой квалификации. Включение
дисциплины «Прикладная экономика» в учебный план студентов, обучающихся по направлению бакалавриата «Профессиональное
обучение (профиль Экономика и управление)»,
служит решению задач
формирования компетентного и конкурентоспособного работника. Прикладная
экономика как наука имеет большое мировоззренческое значение, поскольку вводит
в круг знаний, описывающих рациональное поведение самостоятельных экономических
агентов. Основной целью изучения данной учебной дисциплины является формирование
способностей студентов применять знания, умения и навыки в области
экономической теории для анализа экономических событий и оптимального решения
конкретных практических задач. Построение
моделей позволяет
отображать реальные процессы на уровне
учебно-практического опыта, осваивать технику экономического мышления,
закладывать основы анализа и прогнозирования развития экономических явлений. Овладение
прикладным содержанием предполагает использование теоретических знаний при
разборе конкретных ситуаций из
практики, которые в свою очередь должны и могут быть
смоделированы в условиях академической
системы обучения. Решение прикладных задач, т.е. задач, поставленных вне математики и решаемых
математическими средствами, позволяет в противовес академическим активизировать
обучающегося на всех трех этапах моделирования: формализации, решения внутри
модели, интерпретации. Приведем пример решения такой прикладной задачи на
основе реальной ситуации.
1. Этап
формализации.
В магазине «Атак» каждый день покупатели
желают и приобретают торты
кондитерской компании «Mirel». Причем
спрос таков, что покупатели готовы приобретать каждого вида по одному
экземпляру, в день продается 5-6 тортов.
Продавцы считают, что покупатели отдают предпочтение тортам именно
марки «Mirel», поэтому даже самый дорогой
торт из предлагаемого ассортимента
продается, но либо поздним вечером, либо перед окончанием
срока годности. Торговая фирма
магазина «Атак» завозит торты с учетом интересов
покупателей, при этом, отдавая предпочтение более дорогим видам продукции. В ассортименте тортов марки
«Mirel» имеются торт «Премьера» - по цене 139.30 руб.,
«Муравейник» - по цене 181.20 руб.,
торт «Белиссимо» - 223.60 руб., «Джулия» - 265.80 руб., «Сметанник» - 295.10
руб., «Три шоколада» стоимостью 319.70 руб.
Поскольку менеджеры фирмы считают, что спрос определяет предложение, то
и ассортимент, и ценовой ряд товаров в
магазине должны быть одинаково
широкими. Каждого вида торта
завозят по 5-6 единиц, с учетом их срока хранения 5 дней с даты
изготовления. Практика продаж показала, что в первую очередь продаются торты
более дешевые, исключение составляют праздничные дни. Статистические данные
результатов продажи и покупки тортов в обычный рабочий день представлены в таблице 1 и таблице 2, при этом следует уточнить, что в период закупки тортов «Mirel» на складе
готовой продукции не оказалось торта
«Сметанник».
Определить какое равновесное количество тортов продается в день и
какая цена является равновесной для данного вида продукции.
Таблица 1
Статистические
данные покупок тортов «Mirel» в течение дня
|
P, руб. |
q d, шт. |
Qd, шт. |
|
139.30 |
3 |
10 |
|
181.20 |
1 |
7 |
|
223.60 |
2 |
6 |
|
265.80 |
3 |
4 |
|
295.10 |
0 |
1 |
|
319.70 |
1 |
1 |
Таблица 2
Статистические
данные предложения тортов «Mirel» в течение дня
|
P, руб. |
qs, шт |
Qs,шт |
|
139.30 |
3 |
3 |
|
181.20 |
2 |
5 |
|
223.60 |
5 |
10 |
|
265.80 |
5 |
15 |
|
295.10 |
0 |
15 |
|
319.70 |
5 |
20 |
Прогноз равновесных цены и количества товара в
заданных условиях можно осуществлять с помощью парной регрессии между двумя
переменными – y (в нашем случае)- (Q) и х- (P), т.е.
модели вида :![]()
где y –результирующий показатель, (количество товара,
величина спроса), х – независимая
переменная, фактор-аргумент, (цена). При изучении связей исследуемых признаков
найдем уравнение регрессии. Линейная регрессия сводится к нахождению уравнения
вида: ![]()
2. Решение
внутри модели математическими средствами.
Уравнение вида ![]() позволяет по заданным
значениям фактора x находить теоретические значения результирующего
показателя, подставляя в него фактические значения фактора x. Параметры
уравнения линейной регрессии a и b определяются методом наименьших квадратов:
позволяет по заданным
значениям фактора x находить теоретические значения результирующего
показателя, подставляя в него фактические значения фактора x. Параметры
уравнения линейной регрессии a и b определяются методом наименьших квадратов:
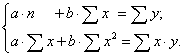
или их можно найти по непосредственным формулам:
![]() ,
, 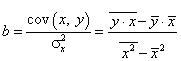 ,
,
где ![]() – ковариация признаков x и y,
– ковариация признаков x и y, ![]() – дисперсия признака x и
– дисперсия признака x и ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]()
![]()
![]() .
.
Для дальнейших вычислений составим расчетную
таблицу (Табл.3) и рассчитаем параметры линейного уравнения регрессии.
Таблица 3
|
|
х(P) |
у(Qd) |
|
|
|
(х- |
(у- |
|
|
1 |
3 |
2 |
4 |
|
5 |
6 |
7 |
9 |
|
1 |
139,30 |
10 |
1393 |
19404,49 |
100 |
9633,423 |
26,698 |
0,517% |
|
2 |
181,20 |
7 |
1268,4 |
32833,44 |
49 |
3164,063 |
4,696 |
0,31% |
|
3 |
223,60 |
6 |
1341,6 |
49996,96 |
36 |
191,823 |
1,362 |
0,195% |
|
4 |
265,80 |
4 |
1063,2 |
70649,64 |
16 |
803,723 |
0,694 |
0,2% |
|
5 |
295,10 |
1 |
295,1 |
87084,01 |
1 |
3323,523 |
14,692 |
3,83% |
|
6 |
319,70 |
1 |
319,7 |
102208,09 |
1 |
6765,06 |
14,692 |
3,83% |
|
Ср.Знач. |
237,45 |
4,83 |
946,83(3) |
60362,77 |
33,83 |
3980,27 |
10,47 |
1,07 % |
|
|
63,089 |
3,236 |
|
|||||
Параметры линейного уравнения регрессии для спроса
Обработка информации позволяет нам получить уравнение: ![]() . Уравнение, обозначенное знаками и символами экономической
науки, будет иметь вид: Qd=16,75−0,05Р
.
. Уравнение, обозначенное знаками и символами экономической
науки, будет иметь вид: Qd=16,75−0,05Р
.
Параметр b называется коэффициентом регрессии.
Его величина показывает среднее изменение результата с изменением фактора на
одну единицу, b=−0,05. Другими
словами, изменение цены на 1 единицу
вызывает изменение количества товара
на 0, 05. Отрицательное значение
коэффициента регрессии с точки зрения
экономики означает обратную зависимость
между признаками, увеличение одной из них приводит к увеличению другой.
Параметр a – значение y (в нашем
случае количество товара- Q) при ![]() (в нашем случае цена -Р). Это, с точки зрения
экономиста, означает, что верхняя величина спроса (количество товара, которое
готовы купить потребители на данном локальном рынке) составляют в нашем
случае 16,75 штук. Поскольку речь идет
о тортах, то можно сказать, что эта величина будет колебаться в различные дни
от 15 до 16единиц. Уравнение регрессии всегда дополняется показателем тесноты
связи. При использовании линейной регрессии в качестве такого показателя
выступает линейный коэффициент корреляции
(в нашем случае цена -Р). Это, с точки зрения
экономиста, означает, что верхняя величина спроса (количество товара, которое
готовы купить потребители на данном локальном рынке) составляют в нашем
случае 16,75 штук. Поскольку речь идет
о тортах, то можно сказать, что эта величина будет колебаться в различные дни
от 15 до 16единиц. Уравнение регрессии всегда дополняется показателем тесноты
связи. При использовании линейной регрессии в качестве такого показателя
выступает линейный коэффициент корреляции ![]() , который можно рассчитать по следующим формулам:
, который можно рассчитать по следующим формулам:
![]() ;
; ![]() -0,05∙
-0,05∙![]() = − 0,975 ;
= − 0,975 ;
где ![]()
![]() ─ дисперсия признака
y,
─ дисперсия признака
y,
![]() ─ дисперсия признака х.
─ дисперсия признака х.
Коэффициент линейной
корреляции находится в пределах:![]() . Близость
коэффициента линейной корреляции к единице указывает на очень тесную линейную
связь между исследуемыми признаками. Квадрат линейного коэффициента корреляции
. Близость
коэффициента линейной корреляции к единице указывает на очень тесную линейную
связь между исследуемыми признаками. Квадрат линейного коэффициента корреляции ![]() , называемый коэффициентом детерминации,
характеризует долю дисперсии результирующего показателя y,
объясняемую регрессией, в общей дисперсии результирующего показателя, т.е.
вызванную влиянием остальных, не учтенных в модели, факторов:
, называемый коэффициентом детерминации,
характеризует долю дисперсии результирующего показателя y,
объясняемую регрессией, в общей дисперсии результирующего показателя, т.е.
вызванную влиянием остальных, не учтенных в модели, факторов: ![]() 0,950, т.е. на долю остальных факторов приходится 0,05%.
0,950, т.е. на долю остальных факторов приходится 0,05%.
О качестве модели можно судить из относительных отклонений по каждому
наблюдению, т.е. определить среднюю ошибку аппроксимации:
![]()
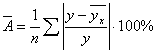
Средняя ошибка аппроксимации не должна превышать 8–10%. В нашем случае
ошибка составляет 1,07 %. Проведем
аналогичные расчеты для уравнения линейной регрессии предложения (Табл.4).
Таблица 4
Параметры линейного уравнения
регрессии для предложения
|
|
x(P) |
y(Qs) |
|
|
|
(х- |
(y- |
|
|
1 |
3 |
2 |
4 |
6 |
5 |
8 |
7 |
9 |
|
1 |
139,30 |
3 |
417,9 |
19404,49 |
9 |
9633,423 |
69, 389 |
2,9% |
|
2 |
181,20 |
5 |
906 |
32833,44 |
25 |
3164,063 |
40,069 |
1,56% |
|
3 |
223,60 |
10 |
2236 |
49996,96 |
100 |
191,823 |
1,768 |
0,193% |
|
4 |
265,80 |
15 |
3987 |
70649,64 |
225 |
803,723 |
13,468 |
0,32% |
|
5 |
295,10 |
15 |
4426,5 |
87084,01 |
225 |
3323,523 |
13,468 |
0,32% |
|
6 |
319,70 |
20 |
6394 |
102208,09 |
400 |
6765,06 |
75,168 |
0, 53% |
|
Ср. Знач. |
237,45 |
11,33(3) |
3061,23 |
60362,771 |
164 |
3980,27 |
61,301 |
1,01% |
|
|
63,089 |
5,963 |
|
|||||
Составим уравнение предложения на основе
параметров уравнения линейной регрессии a и b, которые
определим методом наименьших квадратов:
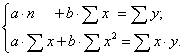
И по непосредственным формулам:
![]() ,
, 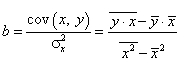 ,
,
![]() ,
, ![]() =−10,04
=−10,04
Тогда уравнение
линейной регрессии для предложения запишем
в следующем виде: Qs = 0,09Р-10,04.
Коэффициент
линейной корреляции ![]() -0,952, что указывает на тесную линейную связь между
исследуемыми признаками, коэффициент
детерминации
-0,952, что указывает на тесную линейную связь между
исследуемыми признаками, коэффициент
детерминации ![]() 0,907, т.е. на долю остальных факторов приходится 0,093%.
0,907, т.е. на долю остальных факторов приходится 0,093%.
Поскольку в условии требуется найти равновесное
состояние рынка указанного товара, то для его нахождения используем
математическое средство- решение системы уравнений, поскольку в точке
равновесия величины спроса и предложения равны между собой. Другими словами,
координаты точки равновесия и по оси Х (в нашем случае Qd=Qs),
и по оси Y (Р). Система уравнений спроса и
предложения:
![]() Qd= 16,81−0,05Р
Qd= 16,81−0,05Р
Qs = 0,09Р-10,04.
Решение системы
уравнений позволяет нам получить координаты точки равновесия на рынке тортов «Mirel» в магазине «Атак» в определенный момент времени
(обычный день): Pe =
196,78 и Qe =6,97.
3. Этап интерпретации.
Результаты, полученные
в задаче, имеют свою интерпретацию. Во-первых, для продавца эти цифры свидетельствуют о ценовой
ориентации потребителя, что позволит маркетологам торговой фирмы прогнозировать
ассортимент продукции. Равновесное количество
равное приближенно 6-7 единицам,
означает, что покупатели готовы купить каждого торта по штуке в день и это
условие будет учтено нами при составлении учебной задачи. Во-вторых, для
покупателя эта информация не менее
ценная, она свидетельствует о том, что покупатель должен прогнозировать свои
покупки в соответствии с доходом и если они низкие, то купить торт ценой в
139.30 можно в день завоза продукции, и хранить его дома в течение срока
годности.
Следует отметить, что
решение этой задачи на графическом калькуляторе позволит получить более точные
результаты и займет считанные
минуты, отображение решения представлено на рис.1-3.


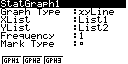
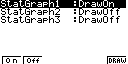
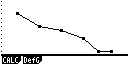
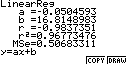
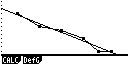


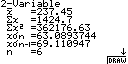
Рис.1. Отображение на дисплее калькулятора последовательности
построения и анализа спроса на рынке
тортов
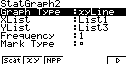

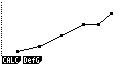
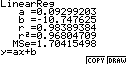
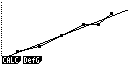

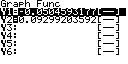
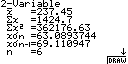
Рис.2. Отображение на дисплее калькулятора последовательности
построения и анализа предложения на
рынке тортов
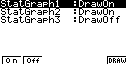
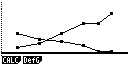

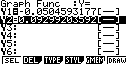
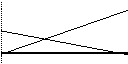
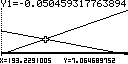
Рис.3. Отображение на дисплее калькулятора последовательности
построения и анализа рыночного равновесия
на рынке тортов
На наш взгляд
решение такой задачи усилит прикладную направленность в процессе
обучения, обеспечит интеграцию различных образовательных областей,
систематизирует их внутреннее слияние,
обеспечивающее углубленное познание общественных процессов.
Литература
1.
Терешин
Н.А. Прикладная направленность школьного курса математики. [Текст] / Н.А.Терешин. — Кн. для
учит. М.: Просвещение, 1990. —96 с.
2.
ФГОС
ВПО по направлению подготовки 44.03.04 Профессиональное обучение (квалификация
«бакалавр») [Электронный ресурс] // Режим доступа:http://www.rsvpu.ru/filedirectory/210/Professional_oby_B_3_dobavleno_27.01.2014.pdf