662.997.517

А.А. КУЧКАРОВ , Ш.И. КЛЫЧЕВ, А.А. АБДУРАХМАНОВ, Ш.Р.ХОЛОВ.

ОПТИКО-ГЕОМЕТРИЧЕСКИЕ параметры ЛИНЕЙНОГО ЗЕРКАЛА ФРЕНЕЛЯ

с плоскими фацетами

Изучены линейные зеркала Френеля (ЛЗФ) с плоскими фацетами. Разработана модель и программа расчета параметров и концентрации ЛЗФ с плоскими фацетами. Показано, что ЛЗФ могут обеспечить концентрацию до 30 крат при числе фацет около 50 с обеспечением высокой равномерности концентрированного излучения на приемнике.

Одной из перспективных областей использования концентраторов считается их применение в установках для получения тепла и пара в диапазоне 100 -200⁰С, а также электроэнергии в СФЭУ при концентрациях от 10 до 30. Основные требования к таким концентраторам это обеспечение достаточно высокой равномерности концентрированного пятнана приемнике. Эти требования могут быть обеспечены линейными фацетными концентраторами. Параметры таких концентраторов с плоскими фацетами на параболоидной основе были рассмотрены в [1]. Недостаток таких концентраторов необходимость достаточно точной до 10 угл. мин. параболоидной основы. В настоящее время для СЭС применяется схема концентратора типа линейных зеркал Френеля (ЛЗФ) со сфероцилиндрическими фацетами. В [2] проведен расчет параметров и концентрирующих характеристик таких ЗФ с параболо- и сфероцилиндрическими фацетами, рассматривалась возможность обеспечения равномерности концентрированного потока.

Целью настоящей работы является определение параметров ЗФ с плоскими фацетами, расположенными на плоской основе и её средних концентраций.

На рис.1 приведена схема ЛЗФ с плоскими фацетами.

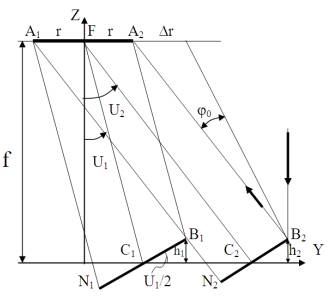
Рис.1. Схема расчета ЛЗФ с плоскими фацетами.

Исходными данными для расчета параметров фацет - ширины L, их расположения (линейные (У_С) и угловые (U_C) координаты центров фацет) являются диаметр (ширина) приемника d и фокусное расстояние f (или обобщенный параметр df = d/f). Расчеты параметров проводятся итерационно, начиная с первой фацеты.

Для первой фацеты считаем, что У_С1= r и имеем

(1)

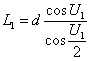, (2)

Для второй и последующих i-ых фацет схема последовательного определения параметров фацет – U_i, У_Сi, L_i имеет вид:

Задаем U_i из уравнения, аналогичного (2) определяем L_i, далее из уравнения (3) определяем

(3)

Из (4) определяем t_A1Ni и У_Ni

(4)

Определяем У_Сi по уравнению (5) и независимо по (6)

(5)

. (6)

Берем их разность и численно решаем до тех пор пока Dу не станет меньше заданного числа. На основе полученных зависимостей был разработан алгоритм и программа определения параметров фацет на языке "Бейсик41". На основе получаемых данных можно определять и площадь зазоров S_з,

(7)

где n – число фацет с одной стороны

Суммарный поток Ф_отр отраженный от ЛЗФ равен

(8)

Прибавка Dr, к радиусу пятна сконцентрированного солнечного излучения за счет конечного углового размера Солнца равна

(9)

где t_A2Nn – расстояние от точки А₂ до верхней точки крайней (i=n) фацеты, или действительный размер солнечного пятна на приемнике буде равно

; (10)

Среднюю концентрацию ЛЗФ с плоскими фацетами C = E/(E_СR_z) (где E – средняя плотность потока сконцентрированного солнечного излучения в пятне, E_С – плотность прямой солнечной радиации и R_z – коэффициент зеркального отражения фацеты), можно представить в виде

(11)

На рис.2. приведены концентрации C ЛЗФ в зависимости от угла раскрытия концентратора U₀ и параметра df.

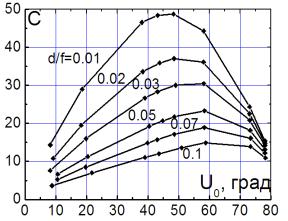
Рис.2. Концентрации С ЛЗФ в зависимости от угла раскрытия U₀ и параметра df.

Из рис.2 видно, что достигаемые концентрации в общем обеспечивают решение указанных выше задач. Так же видно, что и для линейных зеркал Френеля оптимальная концентрация на плоском приемнике при малых df (большое число фацет и их малые размеры) достигается при 45 градусах, с увеличением df (уменьшение числа фацет и соответственно увеличение размеров фацеты) максимум концентрации сдвигается в сторону больших углов раскрытия. Так же видно, что при углах раскрытия больших 75⁰, независимо от df концентрации существенно уменьшаются.

В связ с этим при выборе угла раскрытия концентратора и назначении df необходимо учитывать и другие характеристики ЛЗФ – зазоры, количество фацет, изменение размеров фацет в зависимости от их положения на каркасе. На рис.3. приведены отношение площади зазоров к габаритной площади ЛЗФ (l_З/(2У_n).

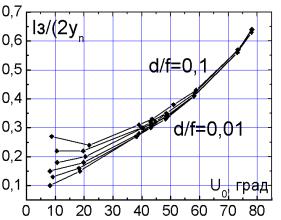
Рис.3. Отношение площади зазоров к габаритной площади ЛЗФ в зависимости от U₀ и df.

Как видно из рис.3. площадь зазоров в ЛЗФ существенна и с увеличением угла раскрытия растет. Можно отметить, что, в общем, параметр df влияет на площадь зазоров, однако практически это величина одного порядка. Зазоры говорят об эффективности использования габаритной площади концентратора, а в случае с ЛЗФ (обычно располагается на земле) зазоры в общем, не существенны.

Изменение размеров фацет, в зависимости от их положения на основе приведены на рис.4.

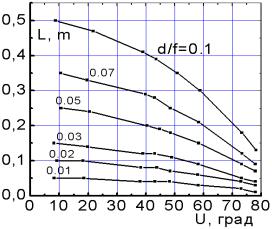
Рис.4. Зависимость размеров (ширины) фацет от положения на основе.

Как видно, при малых df размеры фацет изменяются незначительно, однако с ростом df это изменение необходимо учитывать.

Рис.5. Число фацет в ЛЗФ в зависимости от угла раскрытия и параметра df.

Как видно, число фацет резко возрастает с увеличением угла раскрытия и параметра df. Так же, очевидно, что необходимо стремиться к меньшему числу фацет.

В целом по результатам исследований можно сделать следующие выводы:

1. Разработана модель и программа расчета параметров и концентрации ЛЗФ с плоскими фацетами.

2. ЛЗФ могут обеспечить концентрации до 30 уже при числе фацет около 50 ( по 25 на сторону), а при концентрации 20, число фацет может составлять около 36, при эффективность использования габаритной площади будут на уровне 32%.

3. ЛЗФ с плоскими фацетами могут быть использованы для концентраций до 30 с обеспечением высокой равномерности концентрированного излучения на приемнике (при df =0.07, f = 5м и U₀ около 50⁰ отношение d/d_П составляет 0.76).

ЛИТЕРАТУРА

[1]. Захидов Р.А., Клычев Ш.И., Огнева Т.А., Шульман М.Н. Оптико - энергетические характеристики зеркал Френеля. Гелиотехника, 1990, №4, С 47-50. [2]. Клычев Ш.И., Захидов Р.А., С.А. Бахрамов, Р.А. Хужанов, З.Ш. Клычев. Концентрации линейного зеркала Френеля с ориентируемыми фацетами на неподвижный приемник. Гелиотехника, 2010, №3, С 68-72.