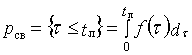Алекина Е.В., Мельникова Д.А., Яговкина Е.Н.

Самарский государственный технический университет, Росиия

Оценка влияния «человеческого фактора» на безопасность при выполнении работ повышенной опасности

При выполнении работ повышенной опасности наиболее частой причиной аварй и несчастных случаев является «человеческий фактор». Условно его можно оценить «надежностью человека», т.е. способностью к сохранению необходимой эффективности работы при усложнении окружающей обстановки.

При оценке надежности человека учитываются следующие факторы [1]: долговременная выносливость – сохранение человеком работоспособности на заданном уровне в течение определенного времени; с нарастанием утомления надежность снижается (наблюдается увеличение неточностей, ошибок, снижение внимания и т.д.);

устойчивость к воздействию факторов внешней среды (температуры, влажности, давления, шума, ускорения), связанная с состоянием нервной системы человека;

работоспособность в экстремальных условиях, т.е. способность принимать правильные решения при дефиците времени, в аварийных ситуациях и пр.;

помехоустойчивость – работоспособность человека в условиях шумов, посторонней речи, движения посторонних предметов в поле зрения; помехоустойчивость человека повышается за счет приобретения опыта работы, тренировок, улучшения условий труда;

спонтанная отвлекаемость – отвлечение внимания в результате внутренних спонтанных колебаний внимания, в первую очередь при длительном пассивном наблюдении;

переключаемость – время «вхождения» в новую деятельность (при этом стереотипные решения предшествующих задач могут переноситься на внось решаемые); определяется индивидуальными особенностями каждого человека.

В ряде случаев человек способствует снижению уровня профессионального риска, что объясняется, например, его способностью восстанавливать сигналы на фоне шумов и своевременно парировать отказы элементов техники.

Надежность человека характеризуется безошибочностью, готовностью, восстанавливаемостью и своевременностью.

Основным показателем безошибочности является её вероятность, которую необходимо вычислять как на уровне отдельной операции, так и на уровне алгоритма в целом.

Для типовых, часто повторяющихся операций в качестве показателя безошибочности можно использовать также интенсивность ошибок, Этот показатель определяют, как правило, в расчете на одну выполненную операцию (алгоритм). По статистическим данным применительно [2]

;

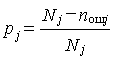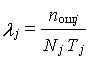
где p_j - вероятность безошибочного выполнения операций j-го вида; λ_j - интенсивность ошибок, допущенных при выполнении операций j- го вида; N_j, n_ошj - общее число выполненных операций j-го вида и допущенное при этом число ошибок;T_j - среднее время выполнения операции j-го вида.

Зная интенсивность ошибок λ_j при выполнении различных операций и алгоритм работы человека, можно найти вероятность безошибочного выполнения этого алгоритма:

(1)

где k_j - число выполненных операций j-го вида;

r - число различных видов операций (j = 1, 2,…, r).

Важным показателем надежности является коэффициент готовности, представляющий собой вероятность включения человека в работу в любой произвольный момент времени и определяемый выражением:

Kоп = 1 – T0/T

(2)

где T₀ - время, в течение которого человек по тем или иным причинам не может принять поступившую к нему информацию; T - общее время работы человека-оператора.

В качестве показателя восстанавливаемости используют вероятность исправления человеком допущенной ошибки:

рисп = ркробнри,

(3)

где р_к - вероятность выдачи сигнала схемой контроля; р_обн - вероятность обнаружения оператором сигнала контроля; р_и - вероятность исправления ошибочных действий при повторном выполнении алгоритма.

Этот показатель позволяет оценить возможность самоконтроля человеком своих действий и исправления допущенных им ошибок.

Показателем своевременности является вероятность выполнения задачи в течение времени τ ≤ t_л, где t_л - лимит времени, превышение которого рассматривается как ошибка. Эта вероятность определяется формулой:

(4)

где f(τ) - функция распределения времени решения задачи человеком.

Время t_л может быть как постоянной, так и случайной величиной. В первом случае вероятность р_св определяется выражением (3). Во втором случае вычисление р_св довольно сложно. Оно упрощается, если τ и t_л подчинены нормальному распределению с параметрами , s_τ и соответственно. Поскольку t_л и τ обычно независимы, то Dt= t_л – τ тоже распределена по нормальному закону с параметрами

, .

На основании известных положений теории вероятности

,

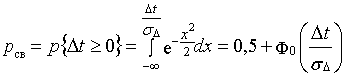где 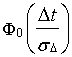- табличное значение функции Лапласа.

Среднее значение времени исправления ошибки

,

где - среднее значение времени исправления ошибки с k-й попытки; p_k - вероятность исправления ошибки с k-й попытки при условии, что в предыдущих k – 1 попытках имела место ошибка.

Такая вероятность подчинена геометрическому распределению вида

p_k = p_оп(1 – р_оп)^k.

Среднее значение времени решения задачи с учетом времени исправления ошибки определяется формулой

(5)

где - среднее значение времени безошибочного выполнения человеком – оператором решения задачи с учетом времени исправления ошибки

(6)

Предположительно можно считать, что время τ_p подчинено нормальному закону распределения с параметрами, определяемыми выражениями (5) и (6). Вероятность своевременного исправления ошибки

p_И(t_л) = р{τ_p < t_л}

определяется в зависимости от характера величины t_л либо выражением (3), либо выражением (4).

Общая вероятность исправления ошибки согласно (2) может быть выражена формулой

р_исп = р_kp_обнр_И(t_л).

Надежность деятельности человека не остается величиной постоянной, а меняется с течением времени. Это изменение обусловлено как изменением условий деятельности, так и колебаниями состояния человека. Поэтому при определении надежности человека в каждом конкретном случае необходимо выбирать те или иные факторы, наиболее характерные для данного вида деятельности. Для каждого из этих состояний находится конкретное значение изучаемого показателя надежности человека.

С учетом рассмотренных положений среднее значение вероятности безошибочной работы человека (при условии независимости появления ошибок)

,

где p_i - вероятность наступления i-го состояния системы «человек-машина»; p_оп/i - условная вероятность безошибочной работы человека в i-м состоянии; m - число рассматриваемых состояний системы«человек-машина».

Вероятности p_i в ряде случаев могут быть определены методами теории массового обслуживания. Вероятности p_оп/i могут быть получены в результате анализа деятельности человека по формуле (1) или экспериментально.

Разработанные положения могут быть использованы при выполнении других видов работ, например, операторской деятельности на опасных производственных объектах

Литература

1. Костюк В.И., Ходаков В.Е. Системы отбражения информации и инженерная психология. Киев: Вища школа, 1977, 192 с

2. Основы инженерной психологии: Учебное пособие/ Под ред. Б.Ф. Ломова.М.:Высшая школа, 1977, 335 с.