Технические науки/4. Транспорт

Д.т.н. Драгунов Г.Д., Лоскутников И.А.

Южно-Уральский государственный университет, Россия

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ РАБОТЫ МЕХАНИЗМА ПЕРЕКЛЮЧЕНИЯ ПЕРЕДАЧ В РАЗДАТОЧНОЙ КОРОБКЕ ДВИЖУЩЕГОСЯ АВТОМОБИЛЯ

Приведено математическое моделирование процесса работы механизма переключения передач в разработанной раздаточной коробке движущегося автомобиля.

Исследование возможностей и путей улучшения эксплуатационных свойств автомобиля в настоящее время можно осуществить на основе использования математической модели (ММ). Для теоретических исследований движения автомобиля обычно используется ММ, сложность которой и характер принимаемых допущений зависят от целей исследования. Для того чтобы разработанная модель наиболее полно и точно соответствовала реальному объекту и решаемой задаче, она должна быть адекватной, полной, точной и устойчивой. Математическая модель механизмов трансформации крутящего момента (М_кр) должна включать зависимости, описывающие переходные процессы в момент переключения передач, уравнения перемещения органов управления и уравнения обратных связей.

Рассмотрим функционирование раздаточные коробки в режиме перехода с высшей передачи на низшую при движении автомобиля. С данным типом переключения водитель наиболее часто сталкивается в процессе эксплуатации автомобиля в сложных дорожных условиях.

Амплитуда и частота возмущающих воздействий со стороны двигателя определяется по суммарной диаграмме его трансформации крутящего момента.

По кинематической схеме, с использованием рабочих чертежей и справочной документации, составлена схема трансмиссии в виде многомассовой системы с безынерционными связями [3]. Момент инерции каждой массы этой системы эквивалентен моменту инерции соответствующей детали. На рисунке фрикционное сцепление изображено в виде фрикциона с моментом М_ф1, а сцепление колесного движителя с почвой представлено в виде фрикциона с моментом М_ф2.

Момент инерции массы, эквивалентный моменту инерции автомобиля, приведенной к ведущему колесу,

J_а =m_a r²_к . (1)

Момент инерции массы, имитирующей массу вращающихся и возвратно-поступательных движущихся элементов двигателя, приведенный к коленчатому валу (в соответствии с рекомендацией В.Н. Болтинского [1]),

J_Д = (1,1…1,2) J_M , (2)

где J_M – момент инерции маховика двигателя.

При определении моментов инерции деталей учитывалась часть массы валов, на которых эти детали установлены. При этом к моменту инерции детали прибавлялось 2/3 момента инерции вала [2]. При расчетах также учитывалась податливость соединительных элементов, а также контактная и угловая податливость зубчатых пар.

В результате приведения реальной схемы трансмиссии к эквивалентной (расчетной) получена сложная, разветвленная схема с большим числом сосредоточенных масс [3]. Анализ такой схемы трудоемок и сложен, поэтому уже на стадии приведения реальной схемы она была упрощена путем уменьшения числа степеней свободы. Предварительно анализируя схему, были выявлены звенья, имеющие малую массу, которые почти не влияют на динамику процесса. Такими звеньями пренебрегали.

Были выделены звенья, работающие при включении передачи. В нашем случае [5] эти массы выделены толстыми линиями. Массы, вращающиеся вхолостую, показаны тонкими линиями, их можно объединить, присоединив к массам, имеющим моменты инерции J₃^’, J₄^’, J₇^’, J₈^’ (рис. 1
J₃ = J₃^’+ J₁₆ + J₁₇ + J₁₈ + J₂₀ , J₄ = J₄^’+ J₁₉ , J₇ = J₇^’ + J₂₁ и J₈ = J₈^’ + J₂₂). Схема существенно упрощается.

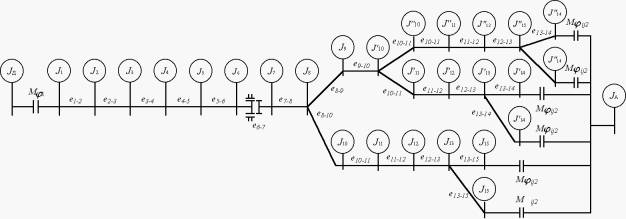
Рис. 1. Упрощенная эквивалентная расчетная схема трансмиссии автомобиля

Все же после предварительного упрощения реальной схемы, приведенная система получается с большим числом масс. Дальнейшее упрощение динамической системы производилось методом парциальных частот.

Таким образом, получена четырехмассовая система (рис. 2), приведенная к первичному валу РК, собственная частота которой определяется уравнением [2].

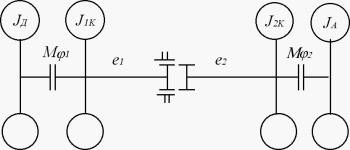
Рис. 2. Приведенная динамическая система

{J_2K ; e₁ }(3)

В результате выполненных преобразований приведенные моменты инерции и податливости деталей трансмиссии можно определить по формулам (3, 4).

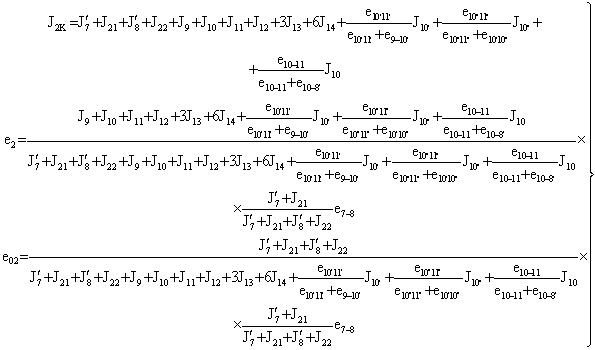
{J_2K ; e₂ } (4)

В качестве обобщенных координат системы принимаем углы закрутки связей φ_i . Все динамические параметры системы приведены к первичному валу раздаточной коробки (РК). Тогда приведенную колебательную систему (рис. 2) можно описать системами дифференциальных уравнений:

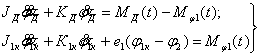(5)

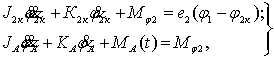(6)

Следует обратить внимание на тот факт, что при установившемся движении автомобиля (при включенном сцеплении и передачах в агрегатах трансмиссии) системы уравнений (5) и (6) следует решать как одну систему из четырех уравнений и лишь при выключенной передаче в РК система из четырех уравнений должна решаться как две системы независимых уравнений.

При отсутствии буксования, или пренебрежением им зависимости (5), преобразуются в следующие уравнения:

; (7)

. (8)

Зависимости (1) - (8) являются математическим моделированием работы трансмиссии автомобиля вообще и механизма переключения передач в РК, в частности.

Литература:

1. Болтинский В. Н. Повышение рабочих скоростей машинно-тракторных агрегатов и задачи науки // Механизация и электрификация социалистического сельского хозяйства. - 1959, № 6.

2. Проектирование трансмиссий автомобилей: Справочник / Под общ. ред. А.И. Гришкевича. – М.: Машиностроение, 1984.

3. Семендяев К.Н. Повышение проходимости полноприводного автомобиля выбором режимов управления раздаточной коробкой. Дис. … канд.техн.наук: – Челябинск, 2003г. 205 с.