К.б.н. Епанчинцева Ольга Михайловна

Кемеровский технологический институт пищевой промышленности, Россия

ИСПОЛЬЗОВАНИЕ ВЕЙВЛЕТОВ МОРЛЕ И ХААРА ДЛЯ ИЗУЧЕНИЯ СТРУКТУРЫ ВОДЫ

Необычные свойства воды обнаруживаются в физико-химических экспериментах. А ее роль в биологических системах вызывает повышенный интерес к изучению структуры воды. Важнейшим показателем качества воды является ее структура, то есть организация ее молекул.

До сих пор было принято оценивать качество воды по двум показателям – это химический и микробиологический состав воды. В настоящее время есть еще одна точка зрения, утверждающая, что структура воды намного более важна, чем ее химический состав.

Вейвлет анализ нашел применение в первую очередь при анализе нестационарных процессов, так как одной из его основных особенностей является возможность получать локализованные характеристики и изучать локальные свойства процессов.

Одним из направлений поиска новых феноменов является анализ обнаружения изменения свойств воды с применением различных вариантов вейвлет-анализа (ВА) [2]. Использование математического аппарата ВА позволило значительно увеличить информативность исследования структурных изменений воды после какой либо ее обработки [2].

В основе непрерывного вейвлет-преобразования [1] сигнала f(t) лежит соотношение

где — вейвлет-образующая функция, из которой с помощью переносов (b — параметр сдвига) и масштабных преобразований (а — параметр масштабирования) строится базис вейвлетов, по которому и раскладывается сигнал f(t),W(a,b)-коэффициенты(амплитуда) вейвлет преобразования. В формуле (2) символом * обозначена процедура комплексного сопряжения. Интегральное преобразование (2) называют непрерывным, если параметры масштаба a и сдвига b, в ходе обработки сигнала, принимают любые действительные значения Оно избыточно по затратам времени на вычисления, но зато позволяет добиться наибольшей детализации при анализе сигналов. Оно ограничено лишь принципом неопределенности.

Функция W(a, b) называется вейвлет-спектром сигнала f(t). Анализ W(a, b) позволяет судить о частотно-временных особенностях сигнала.

Кроме анализа вейвлет-спектров W(a, b), часто рассматривают также и скалограммы и скелетоны. Изучение скалограммы дополняет информацию, содержащуюся в вейвлет-спектре W(a, b),так как исследуются энергетические характеристики сигнала [1].

Некоторые исследователи считают, что в скелетоне заключена вся информация об исследуемом сигнале. Из всех коэффициентов выделяют только значимые, а именно локальные экстремумы, т.е. которые имеют максимумы по переменным а и b. Определение таким образом локальные экстремумы называют скелетоном. Они четко выявляют структуру анализируемого процесса[1]. Их появлением вейвлет- преобразование реагирует на любые негладкости сигнала. Считается, что скелетон не только четко и без лишних деталей визуализирует структуру, но и de facto содержит всю информацию о нем. Скелет максимумов играет важную роль в применении вейвлетов к анализу фракталов. Этих точек очень много обычно в области малых масштабов. Их появлением вейвлет преобразование реагирует на любые негладкости сигнала. При росте масштаба мелкие негладкости исчезают, а вместе с ними и точки максимумов. Оставшиеся сливаются в довольно гладкие кривые, которые при дальнейшем росте масштаба также сливаются друг с другом. При этом они либо «анниглируют», либо продолжают «расти» в область еще более крупных масштабов.

При больших масштабах не учитывается незначительное изменение в анализируемых данных. При построении линий локальных экстремумов задавался минимальный порог, для того, чтобы выявить незначительные изменения сигнала.

Целью настоящей работы являются сравнение динамики поведения локальных максимумов скелетона для динамических сигналов и исследование их изменений при использовании для анализа данных вейвлетов Морле и Хаара.

Было показано, что изменения структуры воды можно увидеть при исследовании динамических сигналов [2]. Для динамических измерений характерно то, что измеряемая величина и время неразрывно связаны в средстве измерений.

Для исследования динамических характеристик были сформирован канал, который состоял из термопреобразователя сопротивления ТСП, измерителя регулятор ТРМ1А компании «Овен».

В качестве исследуемой среды использовалась вода, взятая из водопроводного крана, затем эта же вода повторно.

С помощью вейвлет преобразования нестационарный случайный сигнал анализируется путем разложения по базисным функциям, полученным из некоторого прототипа (материнского вейвлета) путем сжатия (растяжения) и сдвигов. В качестве базисной функции использовался: вейвлет-функция Морле, который обеспечивает минимальное значение частотно-временного разрешения, вейвлет-функция Хаара, который обеспечивает наилучшее разрешение по времени.

Масштабно временной скелет описываемых сигналов представлен на рис.1и 2, где представлены скелетоны динамических сигналов, полученных при исследовании водопроводной воды, взятой из под крана (рис.1.a,b) и этой же воды повторно (рис.2.a,b).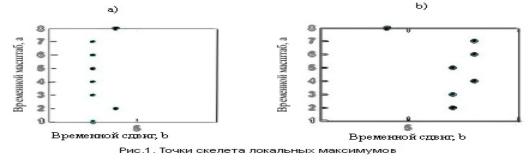

На рис 1 изображены локальные максимумы для водопроводной воды (a) с исользованием вейвлета Морле и того же сигнала с использованием вейвлета Хаара(b).

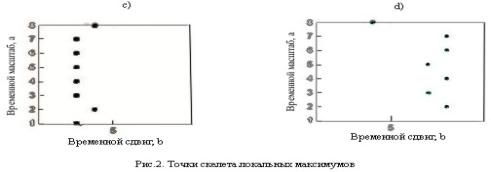
На рис 2 изображены локальные максимумы для той же воды повторно с использованием вейвлета Морле (с) и того же сигнала с использованием вейвлета Хаара(d). Из рисунков 1и 2 видно, что при использовании вевйлета Морле имеется 100% воспроизводимость результата, тогда как для этих же данных вейвлет Хаара показывает изменения.

Таким образом, данные показывают, что внесение теплого термометра в ту же воду уже меняет ее структуру (рис.2.б).

Литература

1. Астафьева Н.М., Вейвлет-анализ: основы теории и применения. Успехи физических наук, 1996, т.166, №11, с.1145-1170

2. Епанчинцева О.М., Использование вейвлет анализа для исследования динамических сигналов //Математические методы в технике и технологиях (ММТТ26), XXVI Международная научная конференция, г. Новгород, 2013, т.8,стр.34-36