Економічні науки/ 8. Математичні методи в економіці

Скрильник І.І., Шумовська Н.О.

Полтавський національний технічний університет, Україна

Побудова прогнозної моделі валового прибутку підприємства «ХейделбергЦемент Україна»

Прогнозування економічних показників підприємства на майбутнє є однією із актуальних задач. Існує ряд класичних методів, що базуються на апараті математичної статистики, серед яких виділяють методи аналізу та моделювання рядів динаміки.

Постановка задачі. На основі статистичних даних за 2010 – 2012 рр. (табл. 1), використовуючи метод аналізу та моделювання ряду динаміки, отримати достовірний прогноз валового прибутку підприємства «ХейделбергЦемент Україна» на перший квартал 2013 р. Провести аналіз результатів та зробити мотивований висновок про якість побудованого прогнозу.

Таблиця 1

Валовий прибуток підприємства за 2010 – 2012 рр.

Рік	Квартал	Прибуток, грн.	Рік	Квартал	Прибуток, грн.
2010	1	55554135,0	2011	1	26976572,0
	2	47390020,0		2	38850120,0
	3	45250900,0		3	41150130,0
	4	42113700,0		4	42320140,0
2012	1	56076876,0	2013	1	прогноз
	2	35130150,0		2
	3	30850640,0		3
	4	27950150,0		4

Розв’язання задачі. Для побудови прогнозної моделі валового прибутку підприємства перевірено гіпотезу про наявність тенденції досліджуваного процесу та виділено тренд. Для цього використано метод рангової кореляції, а також метод Валліса та Мура. За першим методом обчислено коефіцієнт рангової кореляції

, (1)

де – число пар рівнів числового ряду, у яких , , – число рівнів ряду. За результатами розрахунків отримано , що говорить про наявність додатного тренду.

За другим методом фактичне значення критерію розраховано за формулою

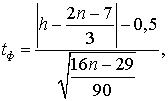(2)

де – число фаз (без першої та останньої). За результатами розрахунку отримано . Табличне значення критерію для даного ряду дорівнює . Отже, ряд має тенденцію, оскільки .

Видалення сезонної складової. Для цього було згладжено часовий ряд методом ковзної середньої та визначено циклічну складову за формулою:

. (3)

Абсолютним відхиленням у сезоні вважається середнє значення циклічних складових року. Розрахунки показали, що сума абсолютних відхилень не дорівнює нулю. У такому випадку було знайдено оцінку сезонних коливань: у 2010 р. – 774779,22 грн.; у 2011 р. – (– 2480408,70 грн.); у 2012 р. – 1778216,19 грн. Далі обчислеі значення ряду з видаленою сезонною компонентою. Обчислені темпи приросту вказуються на те, що компоненти ряду фактичних даних валового доходу мають адитивний зв’язок:

. (4)

Визначення функції тренду. Для вибору кривої зростання застосовано метод характеристик приросту. Відношення першого середнього приросту до є майже постійною величиною, отже, тренд описується функцією виду:

. (5)

Проведено оцінку параметрів моделі. У результаті обчислень отримано, що тренд описується функцією:

. (6)

Обчислено залишки ряду та на їх основі проведено аналіз адекватності побудованої моделі.

Встановлення адекватності моделі. Трендова модель вважається адекватною, якщо вона правильно відображає систематичні компоненти часового ряду, а саме: випадковість, що відповідає нормальному закону розподілу; рівність нулю математичного сподівання; незалежність значень (відсутність автокореляції) [1]. Ці умови повинні виконуватися одночасно.

Для дослідження випадковості відхилень використано метод поворотної точки [2]. Загальне число поворотних точок у ряді залишків дорівнює . Критичне значення визначено за формулою:

(7)

де , . За разрахунками отримано, що . Оскільки , то трендова модель є адекватною.

Для перевірки другої умови визначено t-критерій Стьюдента

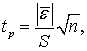(8)

де – математичне сподівання; – стандартне відхилення [2]. Оскільки (, t_р = 0,28), то математичне сподівання випадкової величини дорівнює 0.

Перевірку виконання третьої умови зроблено за допомогою RS-критерія

. (9)

Порівнявши значення RS-критерія з табличними нижніми та верхніми границями, маємо, що . Отже гіпотезу про нормальність розподілення залишків прийнято.

Для перевірки незалежності значень залишкової компоненти використано критерій Дарбіна – Уотсона

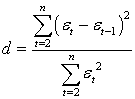. (10)

Отримане значення d=1,43 порівняно з критичними табличними значеннями . Оскільки, 1,36<1,43<2, то можна стверджувати про незалежність залишків. За отриманими значеннями побудовано графік (рис.1).

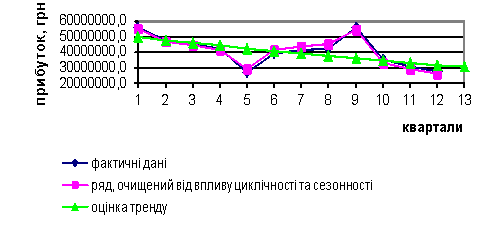
Рис. 1. Графік прогнозу прибутку валового прибутку підприємства «ХейделбергЦемент Україна»

Висновок. Так як усі умови виконалися, то побудована прогнозна модель (6) є адекватною. За даною моделлю визначено прогноз валового прибутку підприємства на перший квартал 2013 р., що становить грн. і знаходиться у межах  грн.

Література:

1. Афанасьев В.Н. Анализ временных рядов и прогнозирование: Учебник. / В.Н. Афанасьев, М.М. Юзбашев. – М.: Финансы и статистика, 2001 – 200 с.

2. Агафонова Н.Ю. Анализ временных рядов. Учебное пособие / Н.Ю. Агафонова. – Саратов, 2010 – 27 с.