К.ф.-м.н. Макаричев А.В., Кудь А.А., Щукин А.Б.

Харьковский национальный автомобильно-дорожный университет

АСИМПТОТИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ ПРОЦЕССА НЕСИММЕТРИЧНОГО СЛУЧАЙНОГО БЛУЖДАНИЯ В МОМЕНТ НАСТУПЛЕНИЯ РЕДКОГО СОБЫТИЯ

Рассмотрим процесс случайного блуждания

,

где случайные величины с вероятностью принимают значения 1 и с вероятностью принимают значение -1 и являются взаимно независимыми, , и ,

Пусть - случайная величина равная с вероятностью , .

Пусть

значение случайного процесса несимметричного блуждания в момент наступления некоторого события, вероятность наступления которого равна .

Теорема. При для любого

.

Доказательство.

Пусть

-

характеристическая функция случайной величины . Найдем характеристическую функцию случайной величины

,

Вычислим математическое ожидание

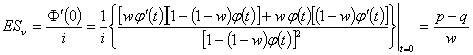
Найдем асимптотическое поведение характеристической функции случайной величины . Имеем

.

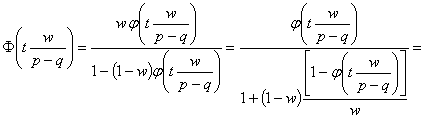
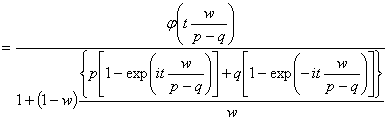При величина для любого , а

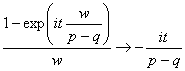При величина для любого , так как

.

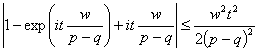Аналогично 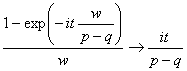при
Отсюда окончательно при для любого

.

Согласно обратной предельной теореме для последовательностей функций распределения и последовательностей их характеристических функций при для любого

,

что и требовалось доказать.

Опираясь на эту теорему, при малых значениях величиныможно находить для любого вероятности

.

Литература.

1. Гнеденко Б.В. Курс теории вероятностей, М., Наука, 1988.

2. Соловьев А.Д. Асимптотическое поведение момента наступления редкого события в регенерирующем процессе. Известия АН СССР. Техническая кибернетика, 1971, № 6, с. 79-89.

3. Ширяев А.Н. Вероятность-М.: Наука, 1980.